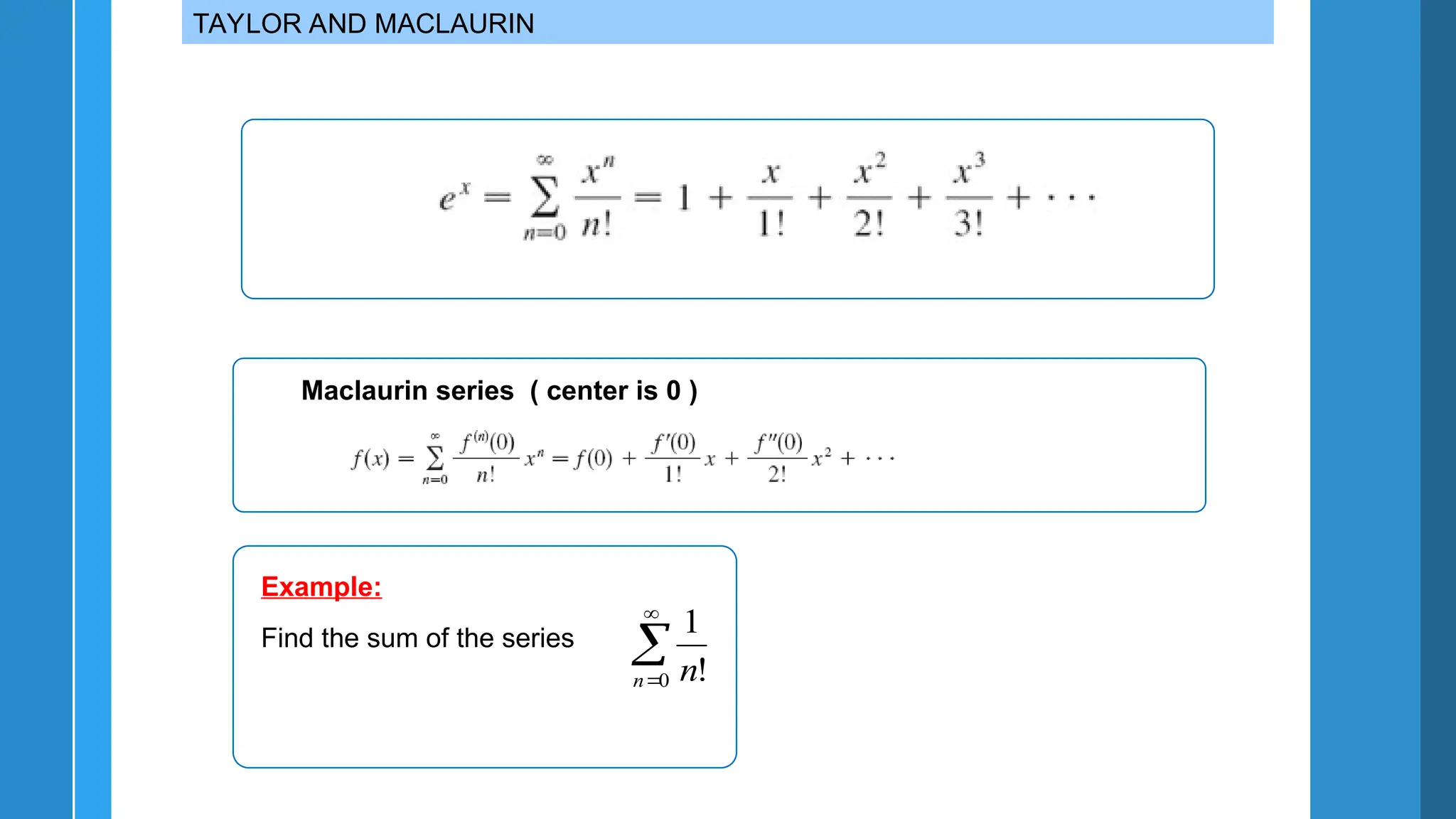
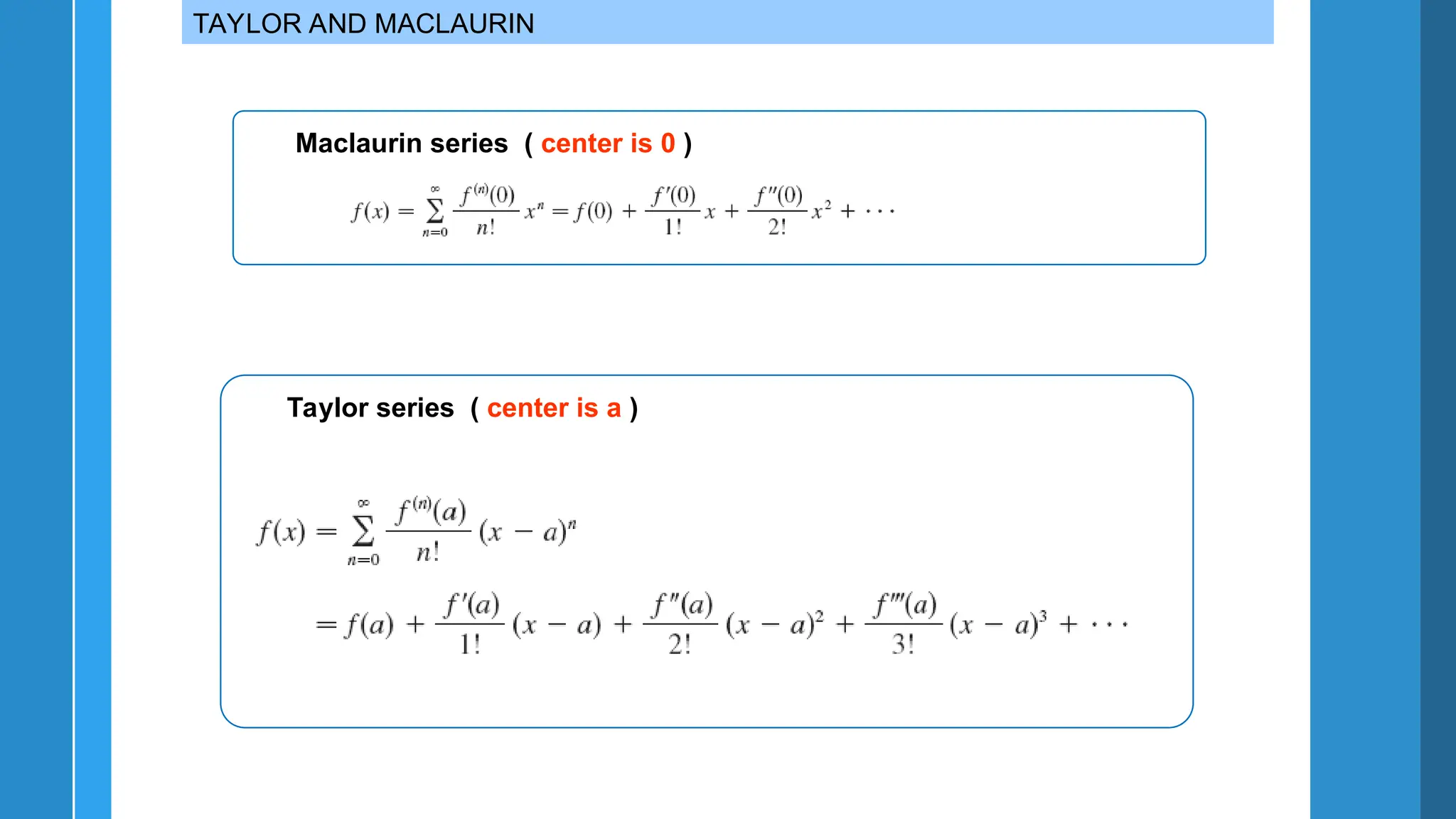
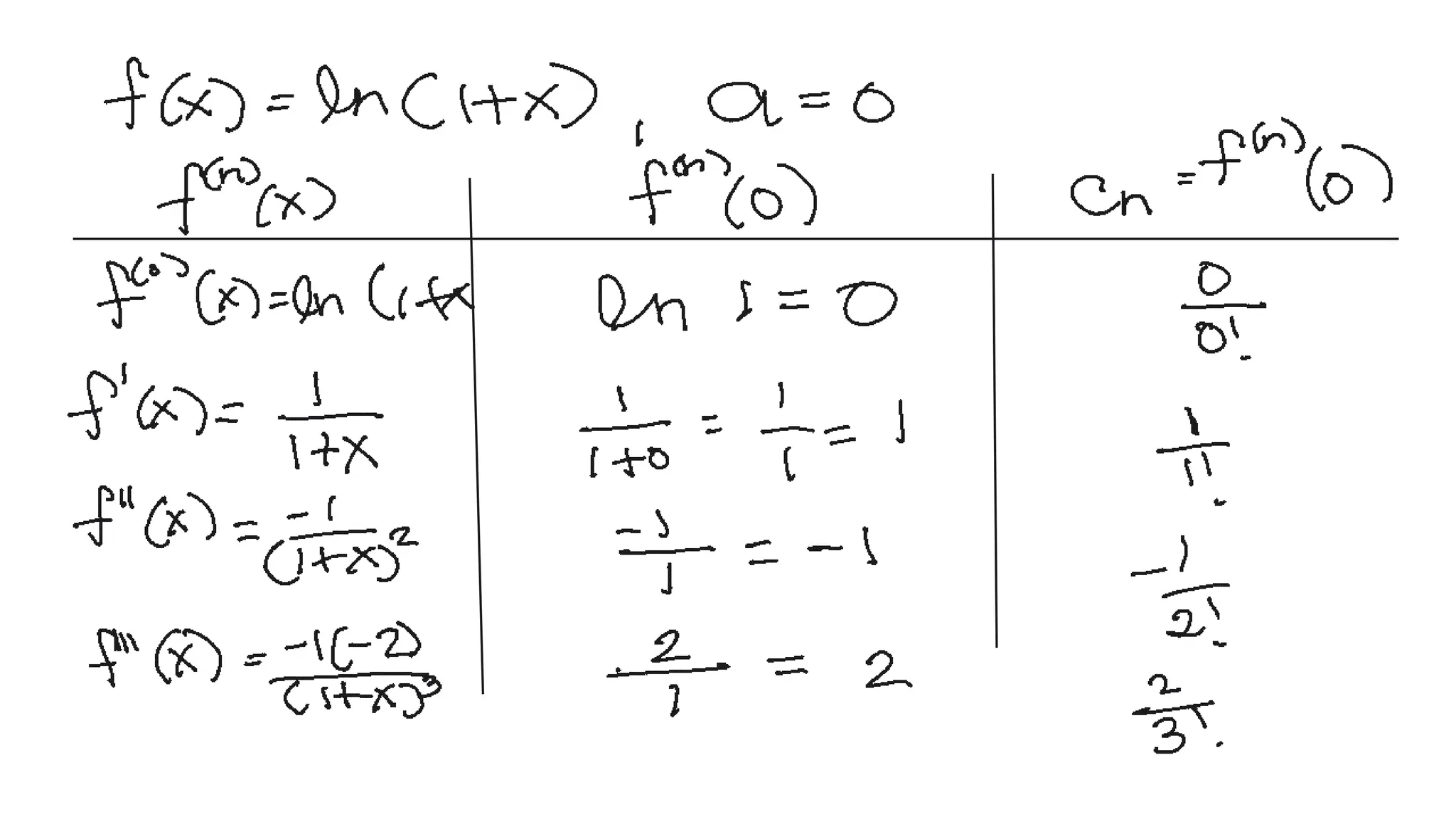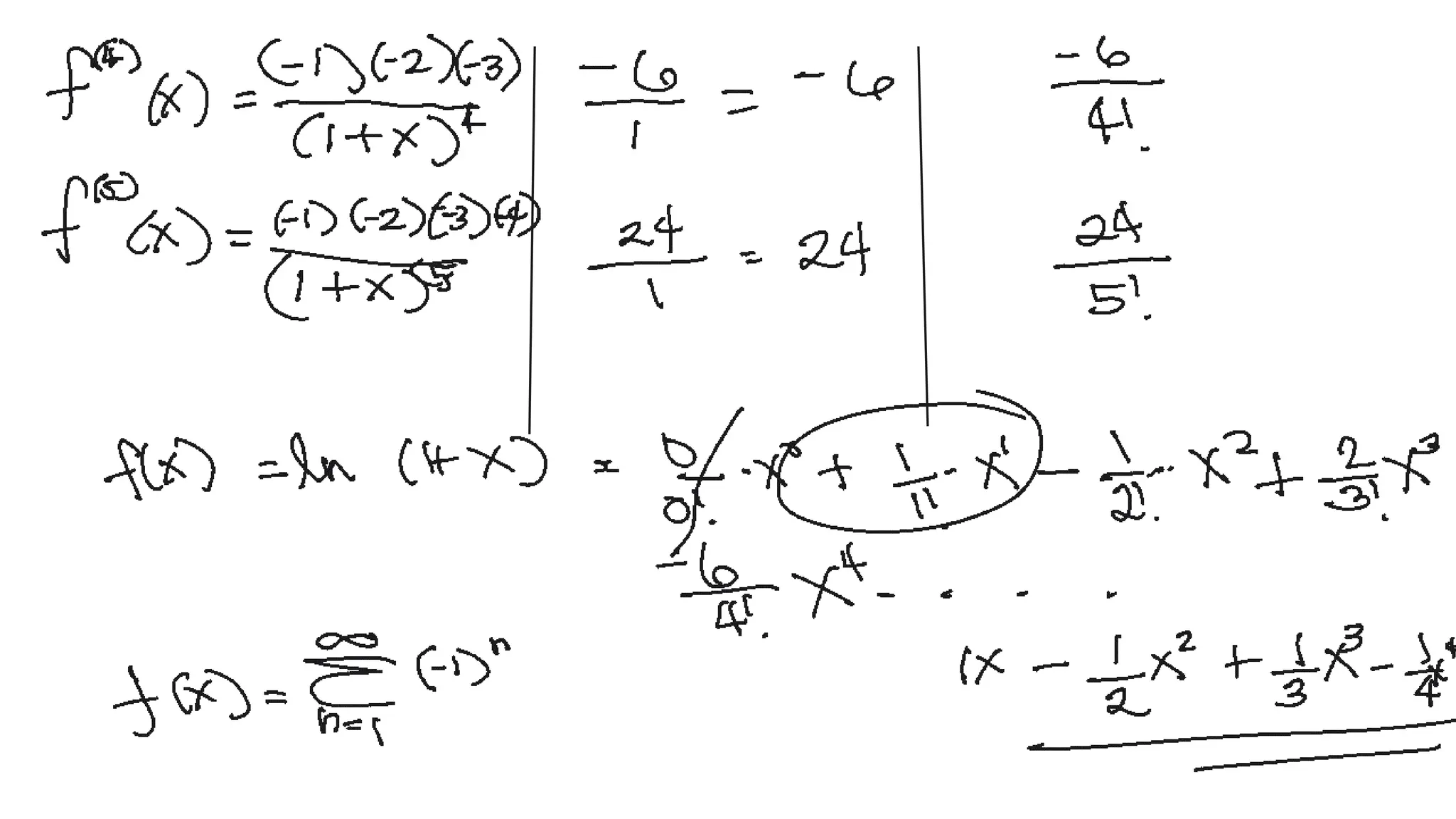The document discusses Taylor and Maclaurin series, which are used to represent functions as sums of power series. It covers the importance of these series in integration, limit finding, and series summation, providing various examples and formulas. Additionally, it emphasizes memorizing key Maclaurin series and their radii of convergence.