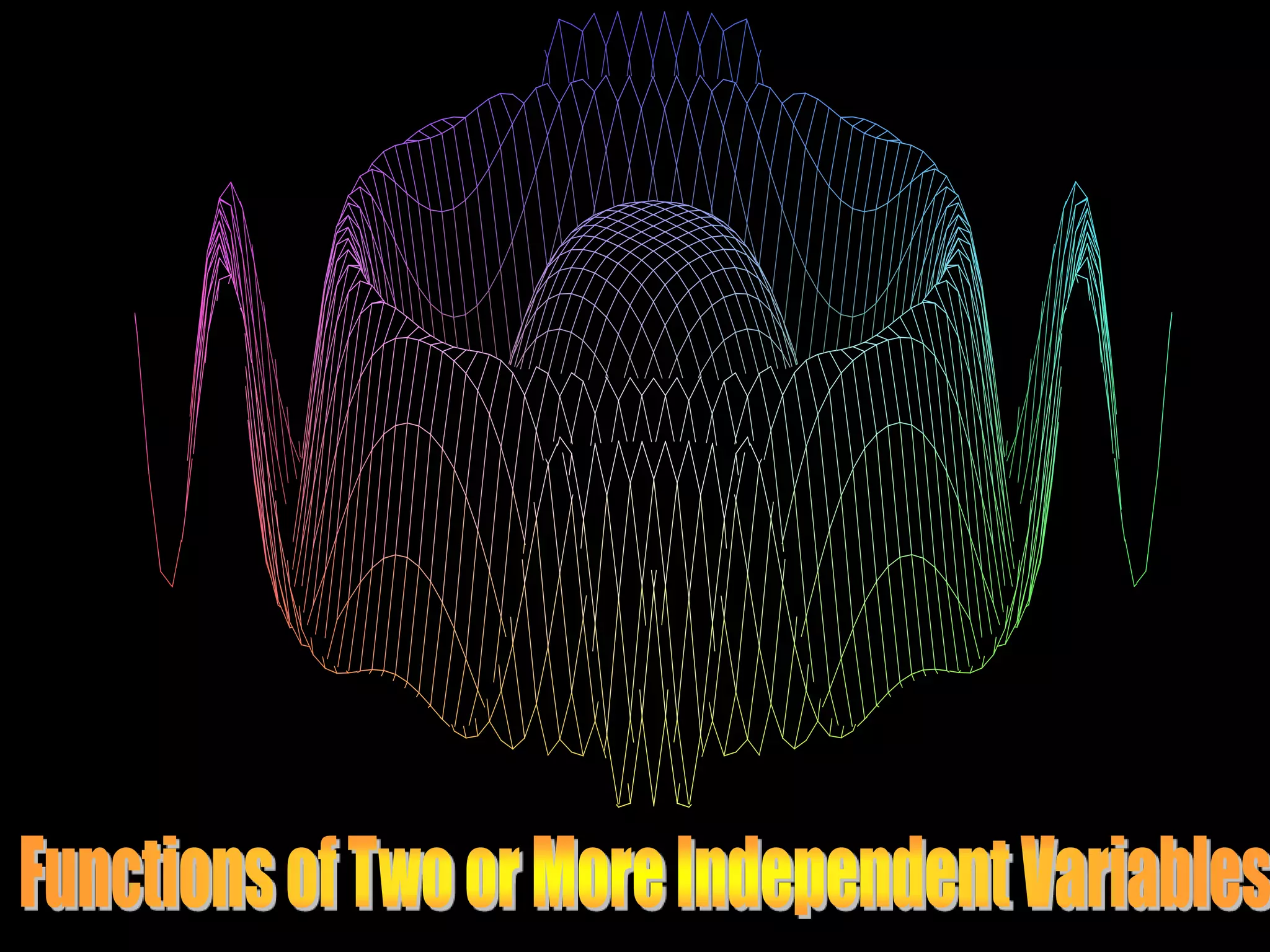
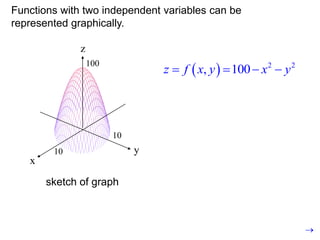
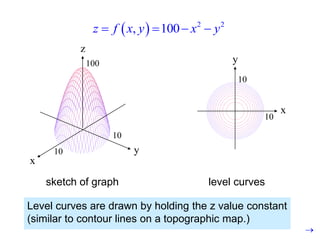
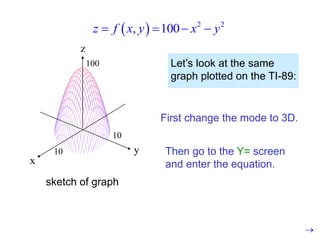
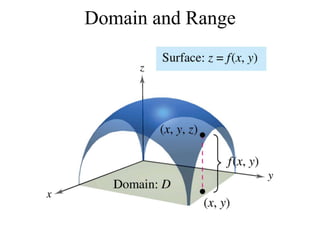
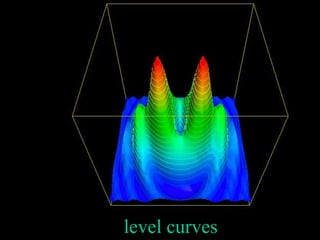
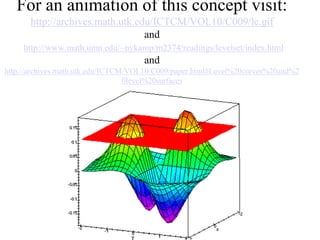
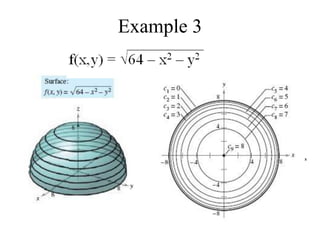
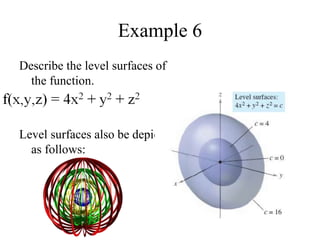
The document discusses functions with more than one independent variable and how to represent them graphically. It introduces the concept of level curves, which are lines connecting points where the function z has a constant value. Level curves are similar to contour lines on a topographic map and can be drawn to sketch the graph of a multi-variable function. The document provides an example of a two-variable function and shows its level curves. It also discusses how to view such graphs using a graphing calculator.

2. The functions that we studied last year were all functions
of one independent variable:
eg:  
   
2
sin
f x x
f x x


In real life, functions often have more than one
independent variable:
eg:
1
Area of a triangle:
2
A bh
  
1
,
2
f b h bh

  2 2 2
, ,
f x y z x y z
   2 2 2
w x y z
  


3. y
x
z
  2 2
, 100
z f x y x y
   
10
10
100
sketch of graph

Functions with two independent variables can be
represented graphically.

4. y
x
z
  2 2
, 100
z f x y x y
   
x
y
10
10
10
10
100
sketch of graph level curves
Level curves are drawn by holding the z value constant
(similar to contour lines on a topographic map.)


5. y
x
z
  2 2
, 100
z f x y x y
   
10
10
100
sketch of graph
Let’s look at the same
graph plotted on the TI-89:
First change the mode to 3D.
Then go to the Y= screen
and enter the equation.


6. Definition of a Function of Two
Variables

7. Domain and Range

8. Example 1 a
Find the domain of the function:
(Solution on next slide)

10. level curves

11. Level Curves
These level curves show lines
of equal elevation above sea
level
Alfred B. Thomas/Earth Scenes
USGS

12. For an animation of this concept visit:
http://archives.math.utk.edu/ICTCM/VOL10/C009/lc.gif
and
http://www.math.umn.edu/~nykamp/m2374/readings/levelset/index.html
and
http://archives.math.utk.edu/ICTCM/VOL10/C009/paper.html#Level%20curves%20and%2
0level%20surfaces

13. Example 3
the hemisphere given by
Draw level curves for z = 0,1,2, ….8

14. Example 3
x

15. Example 6
Describe the level surfaces of the function.

17. Example 6
Describe the level surfaces of
the function.
Level surfaces also be depicted
as follows:

18. Examples of level surfaces:

19. 19
Definition of Continuity of a single variable
• A function is continuous at a point x = c
if the following three conditions are met
1. f(c) is defined
2.
3.
lim ( ) exists
lim ( ) ( )
x c
x c
f x
f x f c



x = c

33. Partial and Total derivatives
For a function of two variables 𝒈(𝒙, 𝒚) ,
the partial derivative with respect to 𝒙 is written

38. Stationary Points (Critical point)
• A stationary point of one variable function,𝒇(𝒙) is a point
where the derivative of that function 𝑑𝑓/𝑑𝑥 = 0
• means the slope of the function at this point is zero
• For a differentiable multivariable function, a point where
all the partial derivatives are zero
• Means that the gradient of the function at this point is
zero.

40. Nature of a Critical point