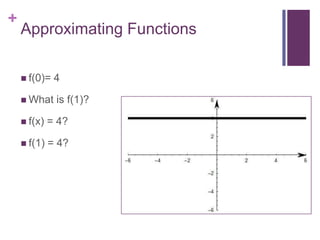
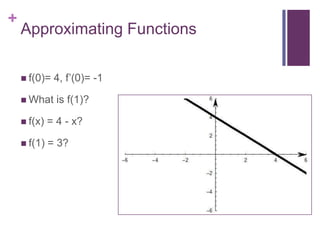
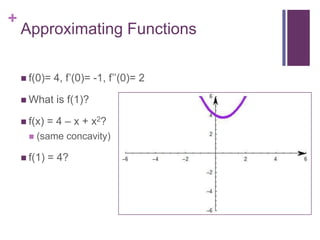
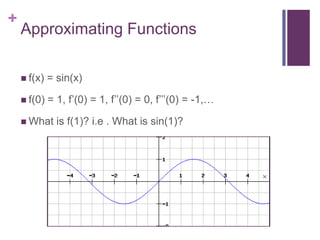
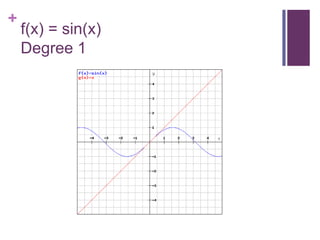
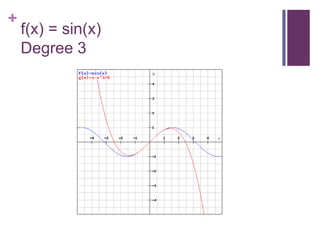
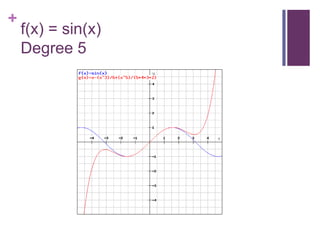
This document discusses Taylor series and their applications. It begins by showing examples of using Taylor series to approximate functions at different points. It then provides background on famous mathematicians who contributed to the development of Taylor series. It explains Taylor's theorem which forms the basis for Taylor series and polynomial approximations. Several proofs are given, including that Taylor series can be used to represent entire functions like sine. Applications of Taylor series discussed include special relativity, optics, physics, and surveying.

1. Taylor SeriesJohn Weiss

2. Approximating Functionsf(0)= 4What is f(1)?f(x) = 4?f(1) = 4?

3. Approximating Functionsf(0)= 4, f’(0)= -1What is f(1)?f(x) = 4 - x?f(1) = 3?

4. Approximating Functionsf(0)= 4, f’(0)= -1, f’’(0)= 2What is f(1)?f(x) = 4 – x + x2? (same concavity)f(1) = 4?

5. Approximating Functionsf(x) = sin(x)What is f(1)?f(0) = 0, f’(0) = 1f(x) = 0 + x?f(1) = 1?

6. Approximating Functionsf(x) = sin(x)f(0) = 1, f’(0) = 1, f’’(0) = 0, f’’’(0) = -1,…What is f(1)? i.e . What is sin(1)?

7. Famous MathematiciansJames Gregory (1671)Brook Taylor (1712)Colin Maclaurin (1698-1746)Joseph-Louis Lagrange (1736-1813)Augustin-Louis Cauchy (1789-1857)

8. ApproximationsLinear ApproximationQuadratic Approximation

9. Taylor’s TheoremLet k≥1 be an integer and be k times differentiable at .Then there exists a function such thatNote: Taylor Polynomial of degree k is:

10. Works for Linear Approximations

11. Works for Quadratic Approximations

12. f(x) = sin(x)Degree 1

13. f(x) = sin(x)Degree 3

14. f(x) = sin(x)Degree 5

15. f(x) = sin(x)Degree 7

16. f(x) = sin(x)Degree 11

17. ImplicationsIf fand g have the same value and all of the same derivatives at a point, then they must be the same function!

18. Proof: If f and g are smooth functions that agree over some interval, they MUST be the same functionLet f and g be two smooth functions that agree for some open interval (a,b), but not over all of RDefine h as the difference, f – g, and note that h is smooth, being the difference of two smooth functions. Also h=0 on (a,b), but h≠0 at other points in RWithout loss of generality, we will form S, the set of all x>a, such that f(x)≠0 Note that a is a lower bound for this set, S, and being a subset of R, S is complete so S has a real greatest lower bound, call it c.c, being a greatest lower bound of S, is also an element of S, since S is closedNow we see that h=0 on (a,c), but h≠0 at c. So, h is discontinuous at c, so then h cannot be smoothThus we have reached a contradiction, and so f and g must agree everywhere!

19. Suppose f(x) can be rewritten as a power series…

20. Entirety (Analytic Functions)A function f(x) is said to be entire if it is equal to its Taylor Series everywhereEntiresin(x)Not Entirelog(1+x)

21. Proof: sin(x) is entireMaclaurin Seriessin(0)=0sin’(0)=1sin’’(0)=0sin’’’(0)=-1sin’’’’(0)=0sin’’’’’(0)=1sin’’’’’’(0)=0… etc.

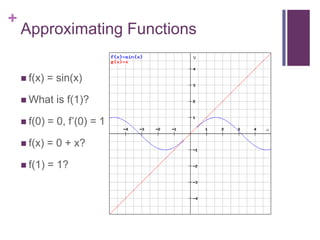
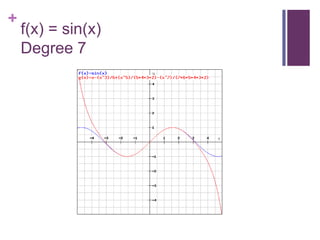
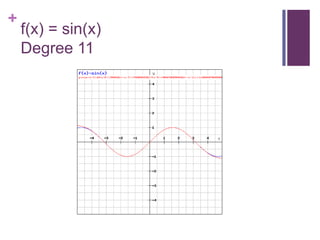
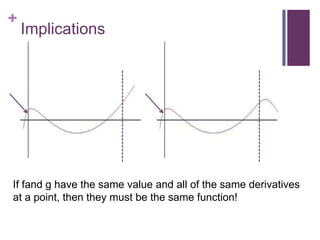
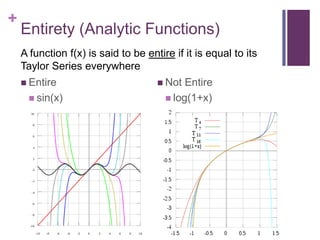
22. Proof: sin(x) is entireLagrange formula for the remainder:Let be k+1 times differentiable on (a,x) and continuous on [a,x]. Then for some z in (a,x)

23. Proof: sin(x) is entire First, sin(x) is continuous and infinitely differentiable over all of RIf we look at the Taylor Polynomial of degree kNote though for all z in R

24. Proof: sin(x) is entireHowever, as k goes to infinity, we seeApplying the Squeeze Theorem to our original equation, we obtain that as k goes to infinityand thus sin(x) is entire since it is equal to its Taylor series

25. Maclaurin Series ExamplesNote:

26. ApplicationsPhysicsSpecial Relativity EquationFermat’s Principle (Optics)Resistivity of WiresElectric DipolesPeriods of PendulumsSurveying (Curvature of the Earth)

27. Special RelativityLet . If v ≤ 100 m/sThen according to Taylor’s Inequality (Lagrange)

28. Lagrange RemainderLagrange formula for the remainder:Let be k+1 times differentiable on (a,x) and continuous on [a,x]. Then for some z in (a,x)

29. Special RelativityLet . If v ≤ 100 m/sThen according to Taylor’s Inequality (Lagrange)

30. The End