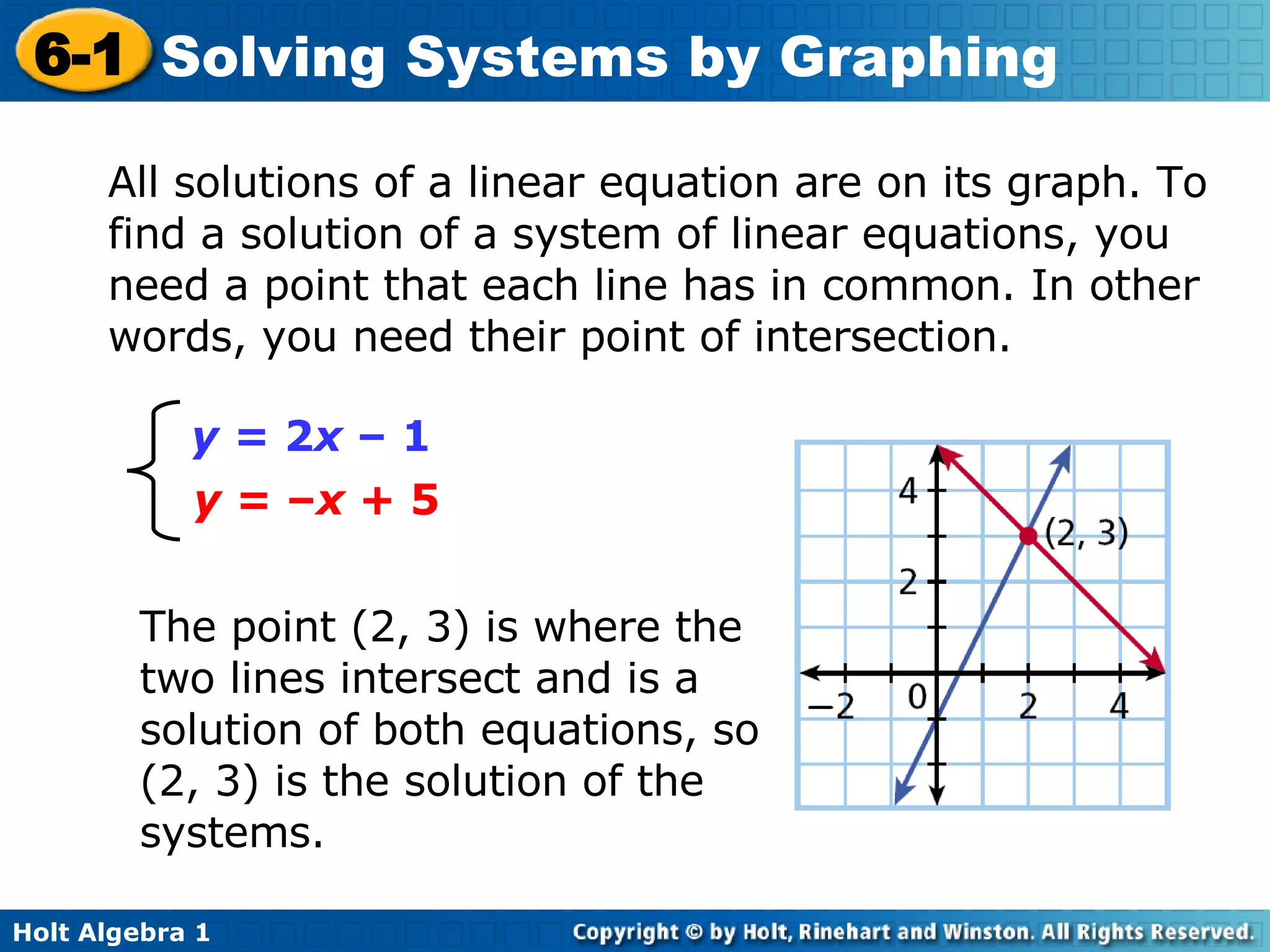
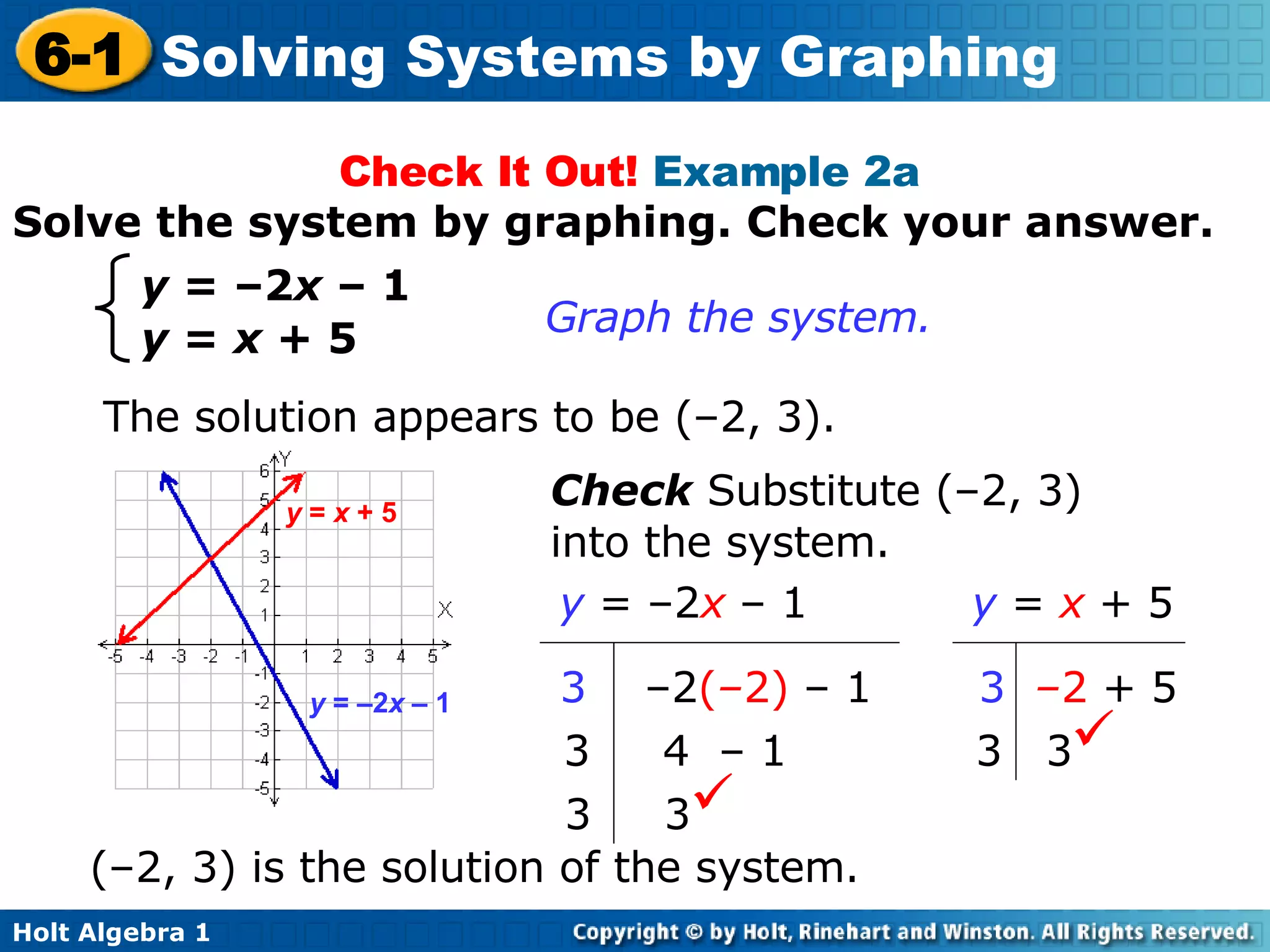
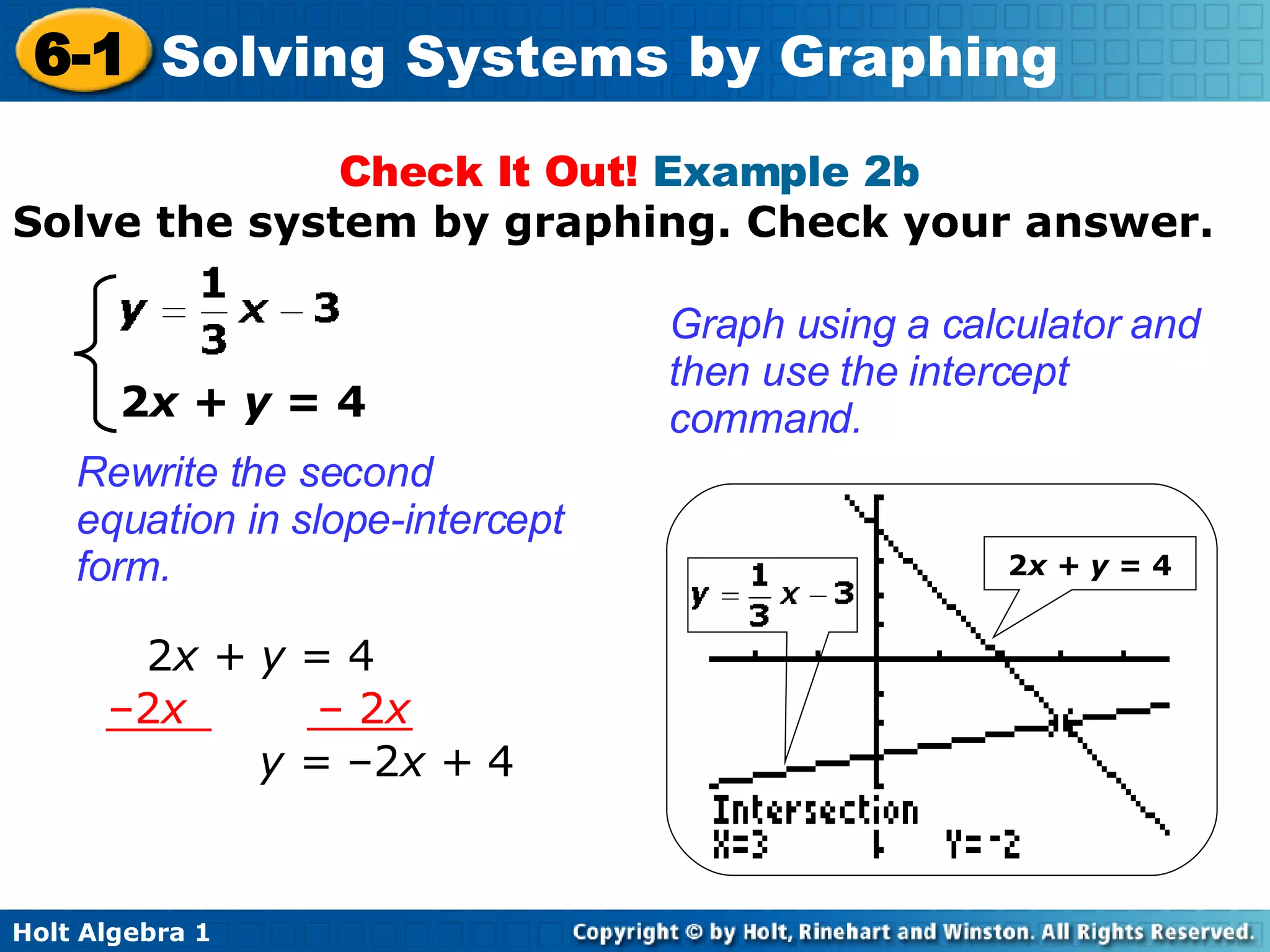
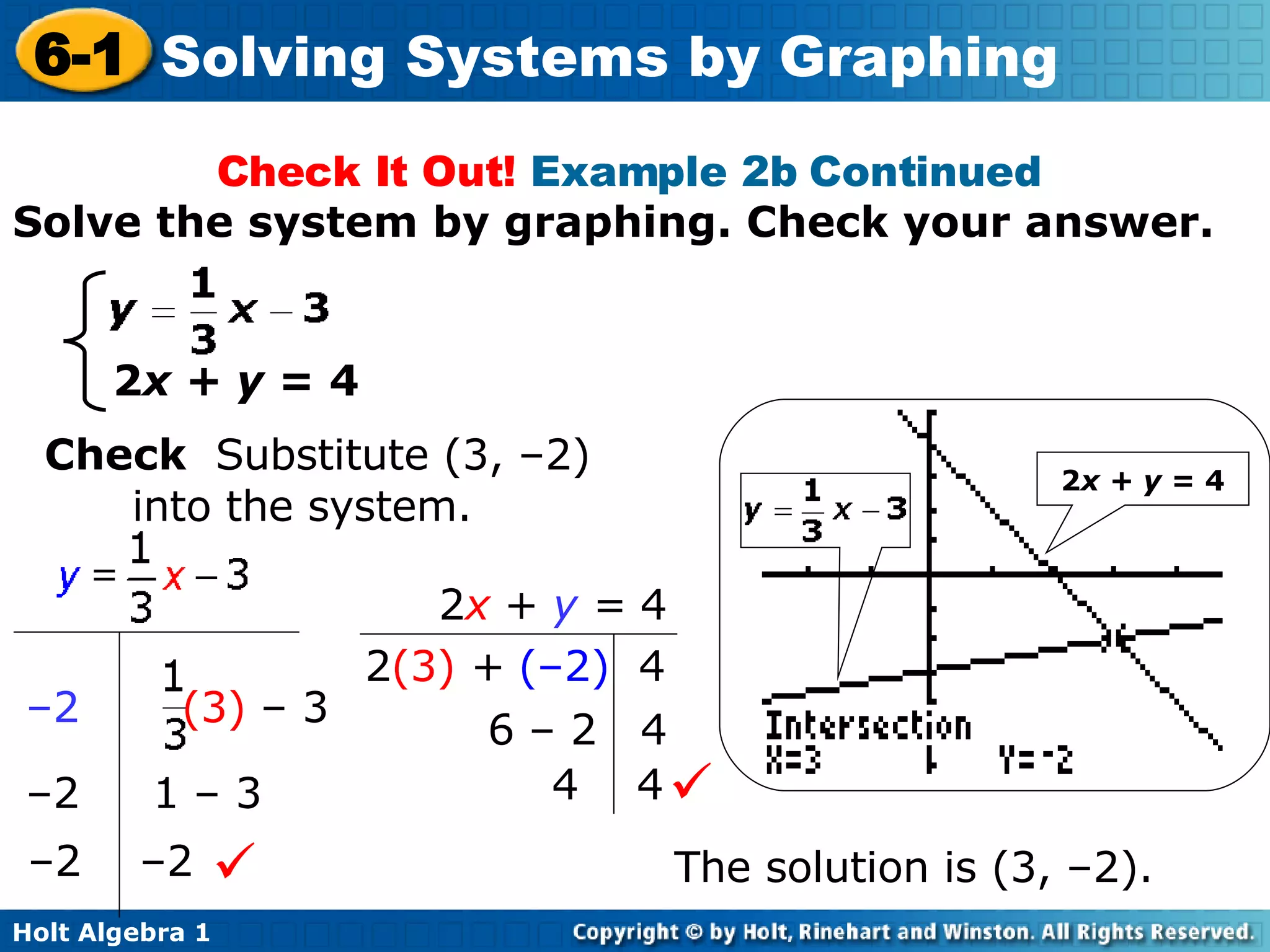
This document provides an overview of solving systems of linear equations by graphing. It begins with examples of identifying whether an ordered pair is a solution to a given system. It then explains that the point of intersection between the graphs of two linear equations is the solution to the corresponding system. The document provides examples of solving systems by graphing and checking solutions by substitution. It concludes with a quiz reviewing the concepts taught.

1. 6-1 Solving Systems by Graphing Holt Algebra 1 Warm Up Lesson Presentation Lesson Quiz

2. Warm Up Evaluate each expression for x = 1 and y =–3. 1. x – 4 y 2. –2 x + y Write each expression in slope-intercept form. 3. y – x = 1 4. 2 x + 3 y = 6 5. 0 = 5 y + 5 x 13 – 5 y = x + 1 y = x + 2 y = – x

3. Identify solutions of linear equations in two variables. Solve systems of linear equations in two variables by graphing. Objectives

4. systems of linear equations solution of a system of linear equations Vocabulary

5. A system of linear equations is a set of two or more linear equations containing two or more variables. A solution of a system of linear equations with two variables is an ordered pair that satisfies each equation in the system. So, if an ordered pair is a solution, it will make both equations true.

6. Tell whether the ordered pair is a solution of the given system. Example 1A: Identifying Systems of Solutions (5, 2); The ordered pair (5, 2) makes both equations true. (5, 2) is the solution of the system. Substitute 5 for x and 2 for y in each equation in the system. 3 x – y = 13 2 – 2 0 0 0  0 3 (5) – 2 13 15 – 2 13 13 13  3 x – y 13

7. If an ordered pair does not satisfy the first equation in the system, there is no reason to check the other equations. Helpful Hint

8. Example 1B: Identifying Systems of Solutions Tell whether the ordered pair is a solution of the given system. (–2, 2); x + 3 y = 4 – x + y = 2 Substitute –2 for x and 2 for y in each equation in the system. The ordered pair (–2, 2) makes one equation true but not the other. (–2, 2) is not a solution of the system.  – 2 + 3 (2) 4 x + 3 y = 4 – 2 + 6 4 4 4 – x + y = 2 – (–2) + 2 2 4 2

9. Check It Out! Example 1a Tell whether the ordered pair is a solution of the given system. The ordered pair (1, 3) makes both equations true. Substitute 1 for x and 3 for y in each equation in the system. (1, 3) is the solution of the system. (1, 3); 2 x + y = 5 – 2 x + y = 1 2 x + y = 5 2 (1) + 3 5 2 + 3 5 5 5  – 2 x + y = 1 – 2 (1) + 3 1 – 2 + 3 1 1 1 

10. Check It Out! Example 1b Tell whether the ordered pair is a solution of the given system. (2, –1); x – 2 y = 4 3 x + y = 6 The ordered pair (2, –1) makes one equation true, but not the other. Substitute 2 for x and –1 for y in each equation in the system. (2, –1) is not a solution of the system. 3 x + y = 6 3 (2) + (–1) 6 6 – 1 6 5 6 x – 2 y = 4 2 – 2 (–1) 4 2 + 2 4  4 4

11. All solutions of a linear equation are on its graph. To find a solution of a system of linear equations, you need a point that each line has in common. In other words, you need their point of intersection. The point (2, 3) is where the two lines intersect and is a solution of both equations, so (2, 3) is the solution of the systems. y = 2 x – 1 y = – x + 5

12. Sometimes it is difficult to tell exactly where the lines cross when you solve by graphing. It is good to confirm your answer by substituting it into both equations. Helpful Hint

13. Solve the system by graphing. Check your answer. Example 2A: Solving a System Equations by Graphing y = x y = –2 x – 3 Graph the system. The solution appears to be at (–1, –1). (–1, –1) is the solution of the system. y = x y = –2 x – 3 • (–1, –1) Check Substitute (–1, –1) into the system. y = x (–1) (–1) – 1 –1  y = –2 x – 3 ( – 1) –2 ( – 1) –3 – 1 2 – 3 – 1 – 1 

14. Solve the system by graphing. Check your answer. Example 2B: Solving a System Equations by Graphing y = x – 6 Rewrite the second equation in slope-intercept form. Graph using a calculator and then use the intercept command. y + x = –1 y = x – 6 y + x = –1 − x − x y =

15. Solve the system by graphing. Check your answer. Example 2B Continued Check Substitute into the system. y = x – 6 The solution is . + – 1 – 1 – 1 – 1 – 1  y = x – 6 – 6 

16. Solve the system by graphing. Check your answer. Check It Out! Example 2a y = –2 x – 1 y = x + 5 Graph the system. The solution appears to be (–2, 3). Check Substitute (–2, 3) into the system. (–2, 3) is the solution of the system. y = x + 5 3 – 2 + 5 3 3  y = –2 x – 1 3 –2 ( – 2) – 1 3 4 – 1 3 3  y = x + 5 y = –2 x – 1

17. Solve the system by graphing. Check your answer. Check It Out! Example 2b 2 x + y = 4 Rewrite the second equation in slope-intercept form. Graph using a calculator and then use the intercept command. 2 x + y = 4 – 2 x – 2 x y = –2 x + 4 2 x + y = 4

18. Solve the system by graphing. Check your answer. Check It Out! Example 2b Continued 2 x + y = 4 The solution is (3, –2). Check Substitute (3, –2) into the system. 2 x + y = 4 2 (3) + (–2) 4 6 – 2 4 4 4  2 x + y = 4 – 2 (3) – 3 – 2 1 – 3 – 2 –2 

19. Lesson Quiz: Part I Tell whether the ordered pair is a solution of the given system. 1. (–3, 1); 2. (2, –4); yes no

20. Lesson Quiz: Part II Solve the system by graphing. 3. (2, 5) y + 2 x = 9 y = 4 x – 3