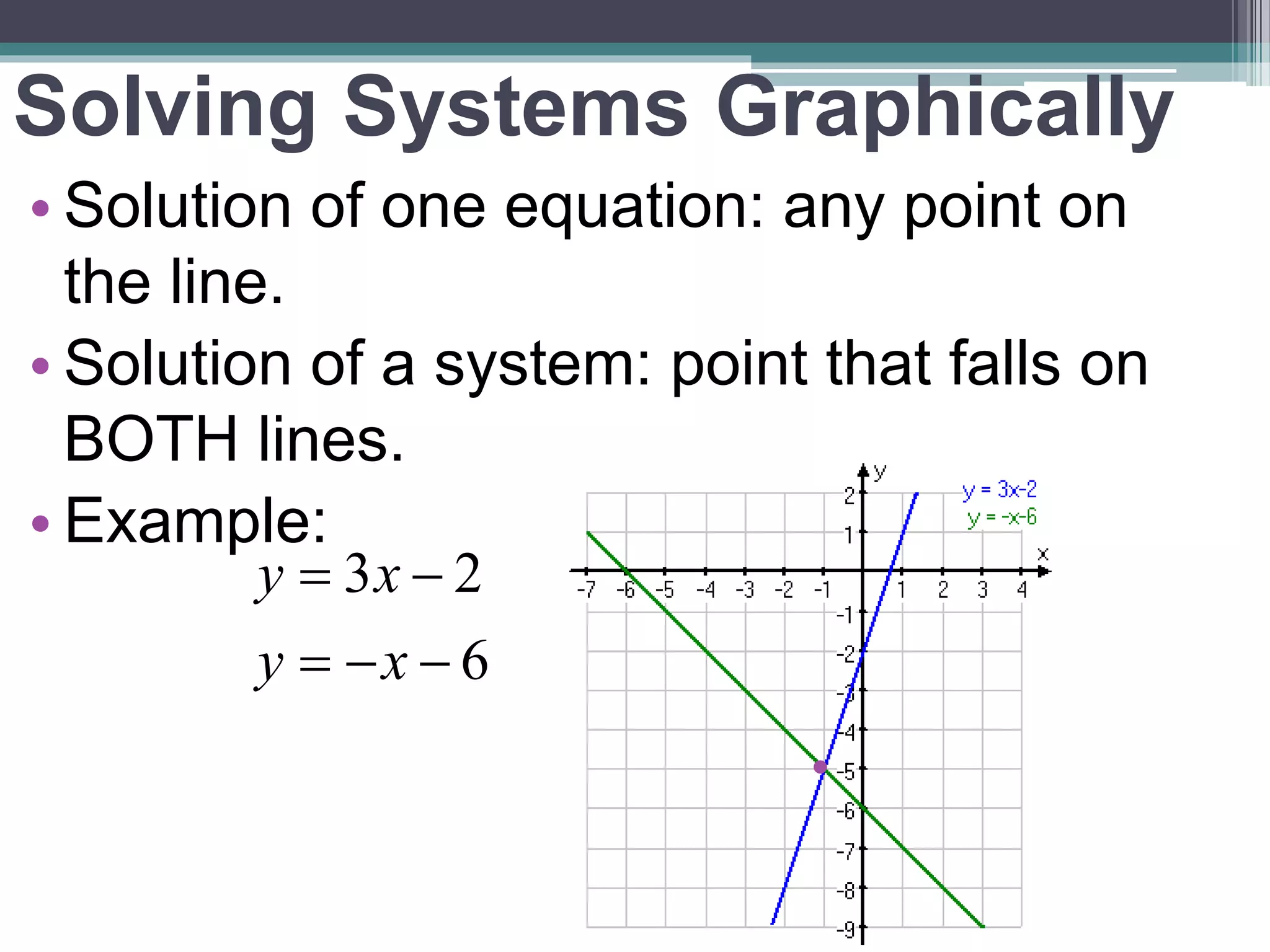
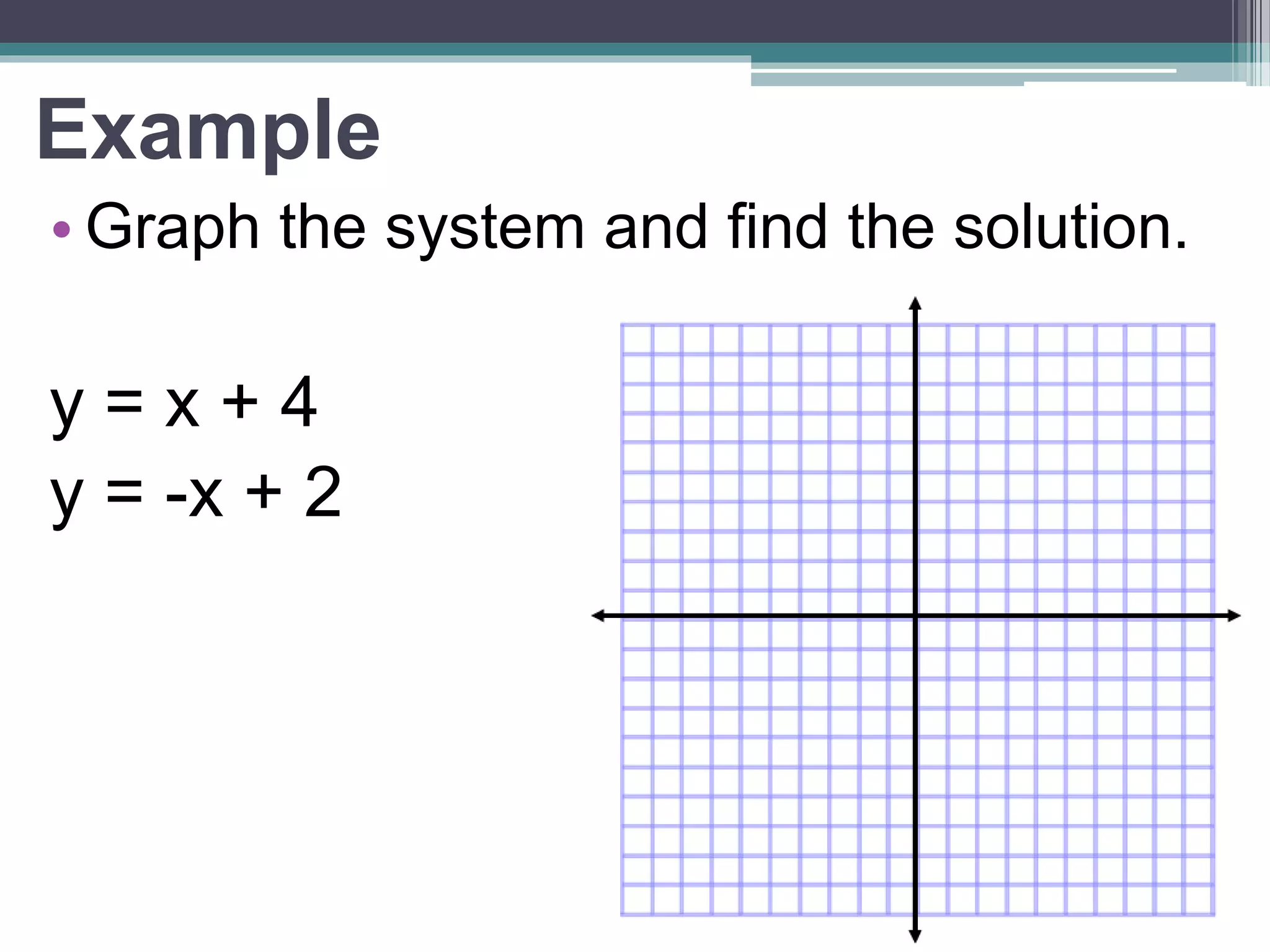
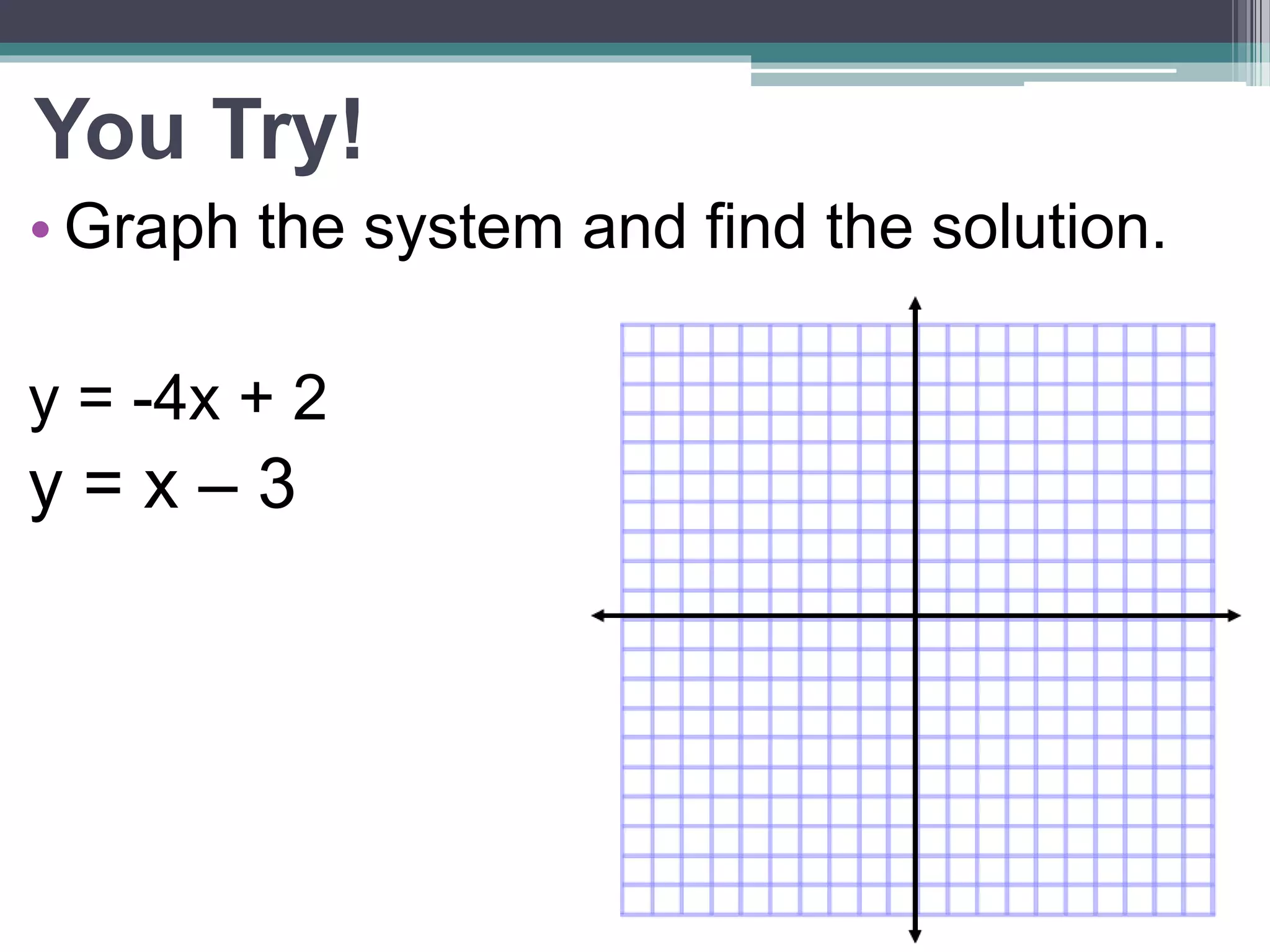
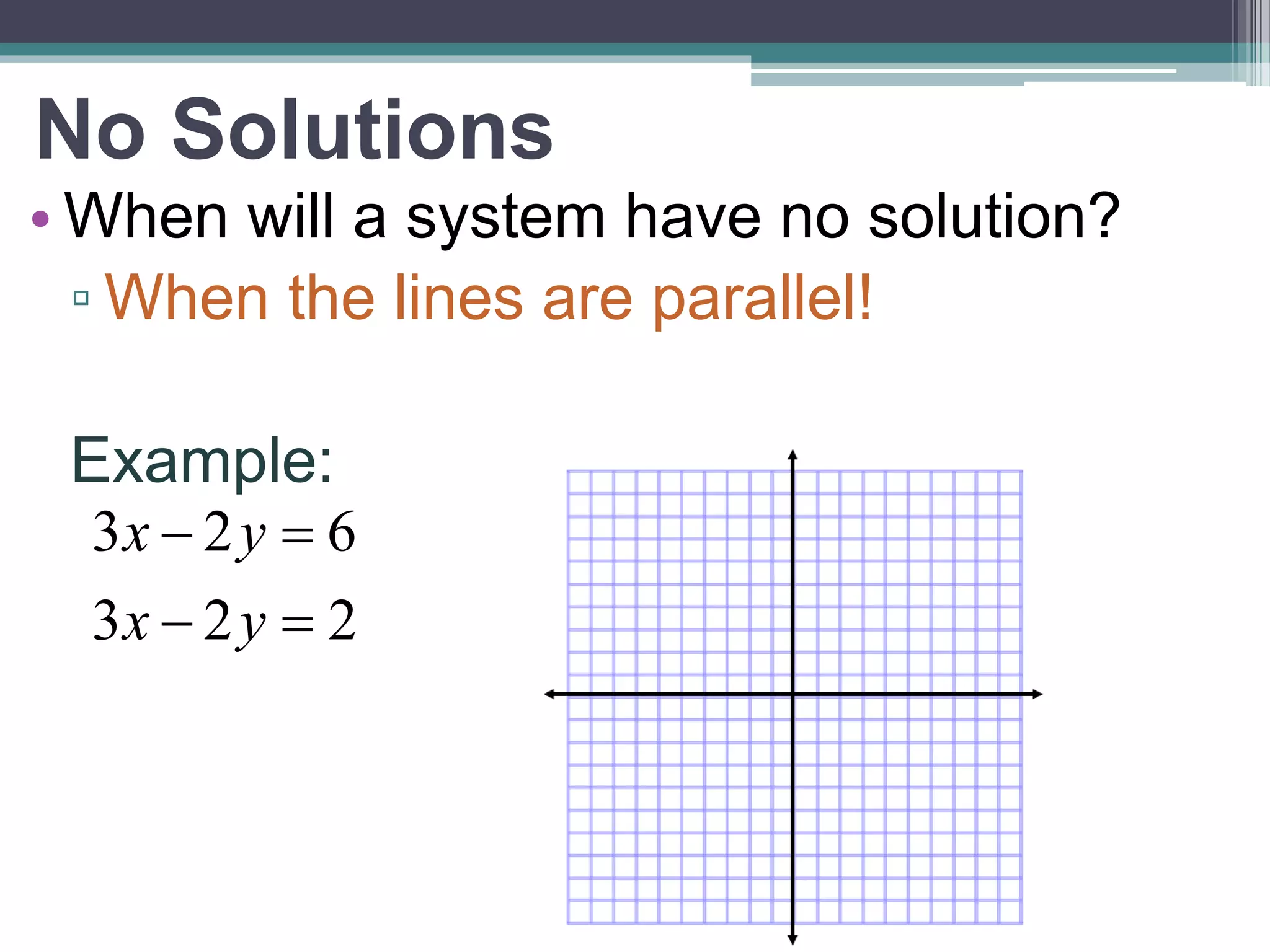
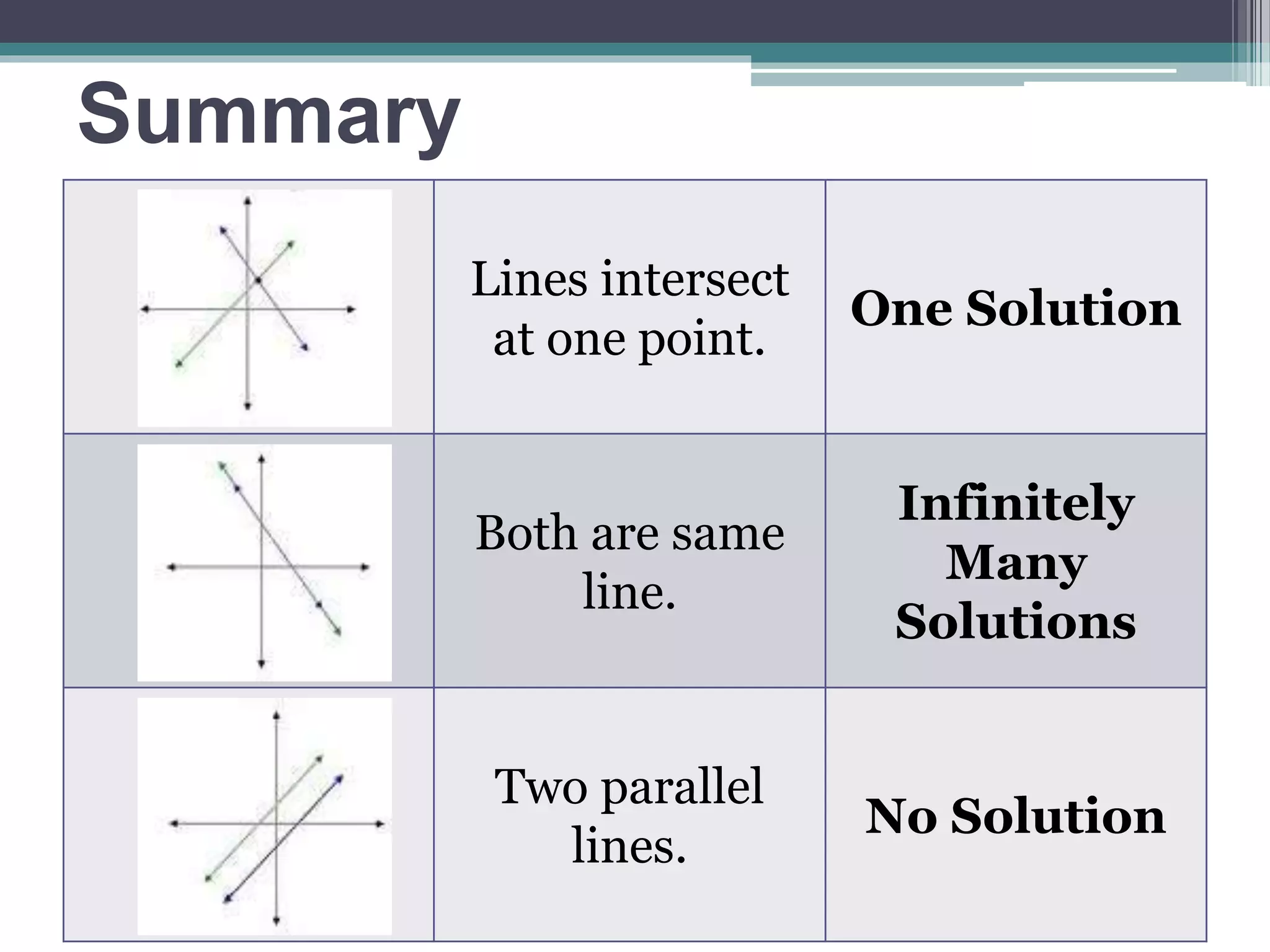
This document discusses linear systems and methods for solving them. A linear system is a set of linear equations where a solution is an ordered pair that satisfies both equations. Graphically, the solution is the point where the lines intersect. Systems can have one solution, infinitely many solutions if the lines are the same, or no solution if the lines are parallel. The document presents two methods for algebraically solving systems: substitution and elimination. Substitution involves solving one equation for a variable and substituting it into the other equation. Elimination involves adding or subtracting equations to eliminate a variable.

1. 1.8 Linear Systems

2. What is a Linear System?
•A set or collection of linear equations.
• A solution of the system is an ordered
pair (x, y) that makes BOTH equations
true.

3. Checking Solutions
• Example:
• Is (2, 2) a solution of the system?
x y
3  2 
2
x  2 y

6
• Is (0, -1) a solution?

4. Solving Systems Graphically
• Solution of one equation: any point on
the line.
• Solution of a system: point that falls on
BOTH lines.
• Example:
y x
3 2
  
6
 
y x

5. Example
• Graph the system and find the solution.
y = x + 4
y = -x + 2

6. You Try!
• Graph the system and find the solution.
y = -4x + 2
y = x – 3

7. Many Solutions
• When will a system have infinitely many
solutions?
▫ When both equations are the same
line!
Example:
x y
3 2 6
 
x y
6  4 
12

8. No Solutions
• When will a system have no solution?
▫ When the lines are parallel!
Example:
x y
3 2 6
 
x y
3  2 
2

9. Lines intersect
at one point.
One Solution
Both are same
line.
Infinitely
Many
Solutions
Two parallel
lines.
No Solution
Summary

10. Substitution Method
Example:
3x + 4y = -4
x + 2y = 2
• 1. Solve one
equation for one
variable.
• 2. Substitute that into
the other equation
and solve.
• 3. Plug in answer and
solve for the other
variable.

11. Example 2
• Solve using substitution.
2x – 3y = -1
y = x – 1

12. You Try!
• Solve the linear system using substitution.
3x – y = 13
2x + 2y = -10

13. Elimination Method
Example:
-3x + 7y = -16
-9x + 5y = 16
• 1. Look for a variable that
will cancel if equations are
added.
• 2. If none, multiply one or
both equations by a
constant.
• 3. Add equations to
eliminate one variable.
Solve for the other.
• 4. Plug it in to solve for
other variable.

14. Example:
• Solve the system using elimination.
7x + 2y = 24
8x + 2y = 30

15. You Try!
• Solve the system using elimination.
3x + 2y = 6
-6x - 3y = -6

16. Example:
• Solve the system.
7x - 12y = -22
-5x + 8y = 14

17. You Try!
• Solve the system using elimination.
9x – 5y = -7
-6x + 4y = 2