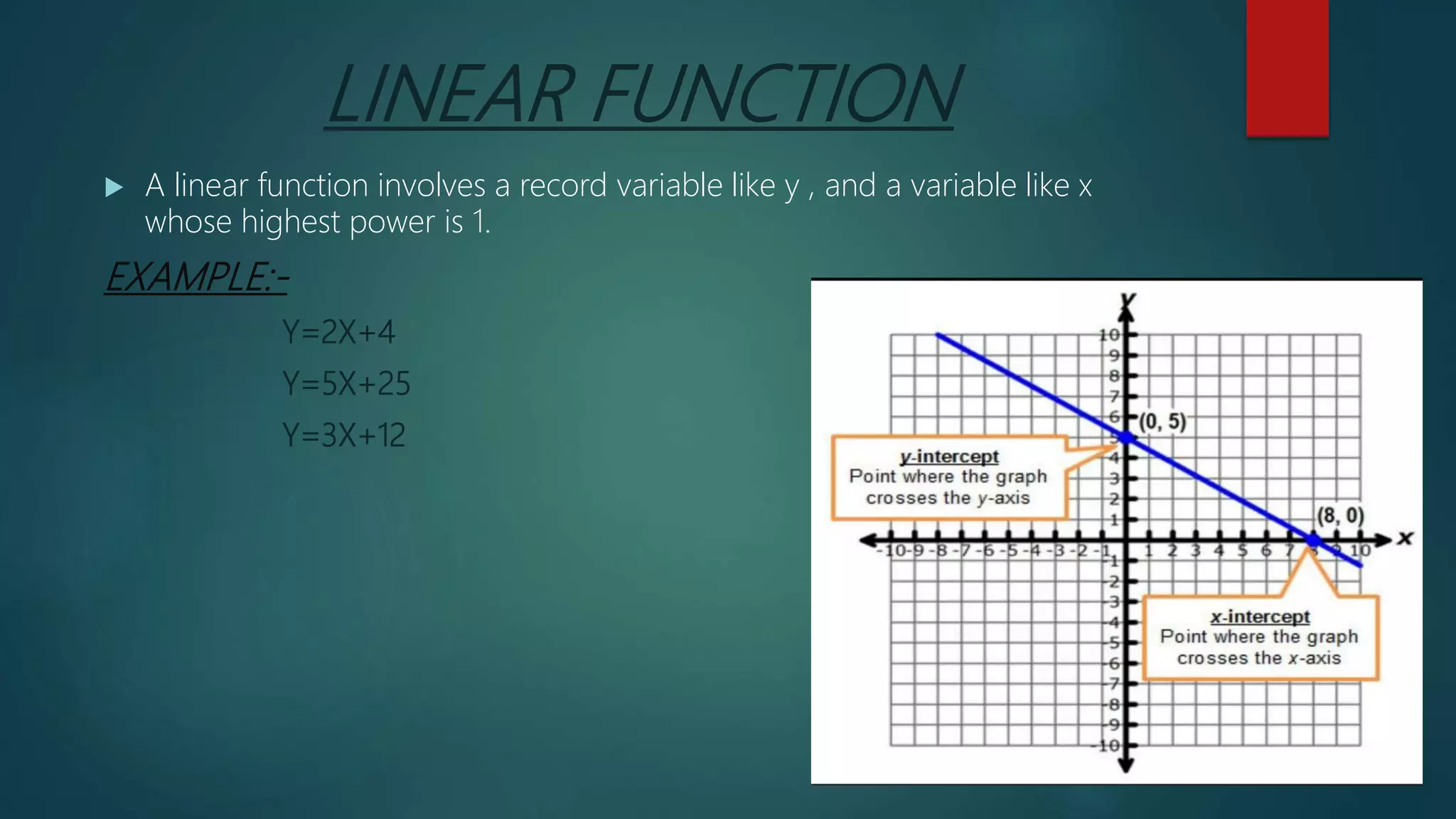
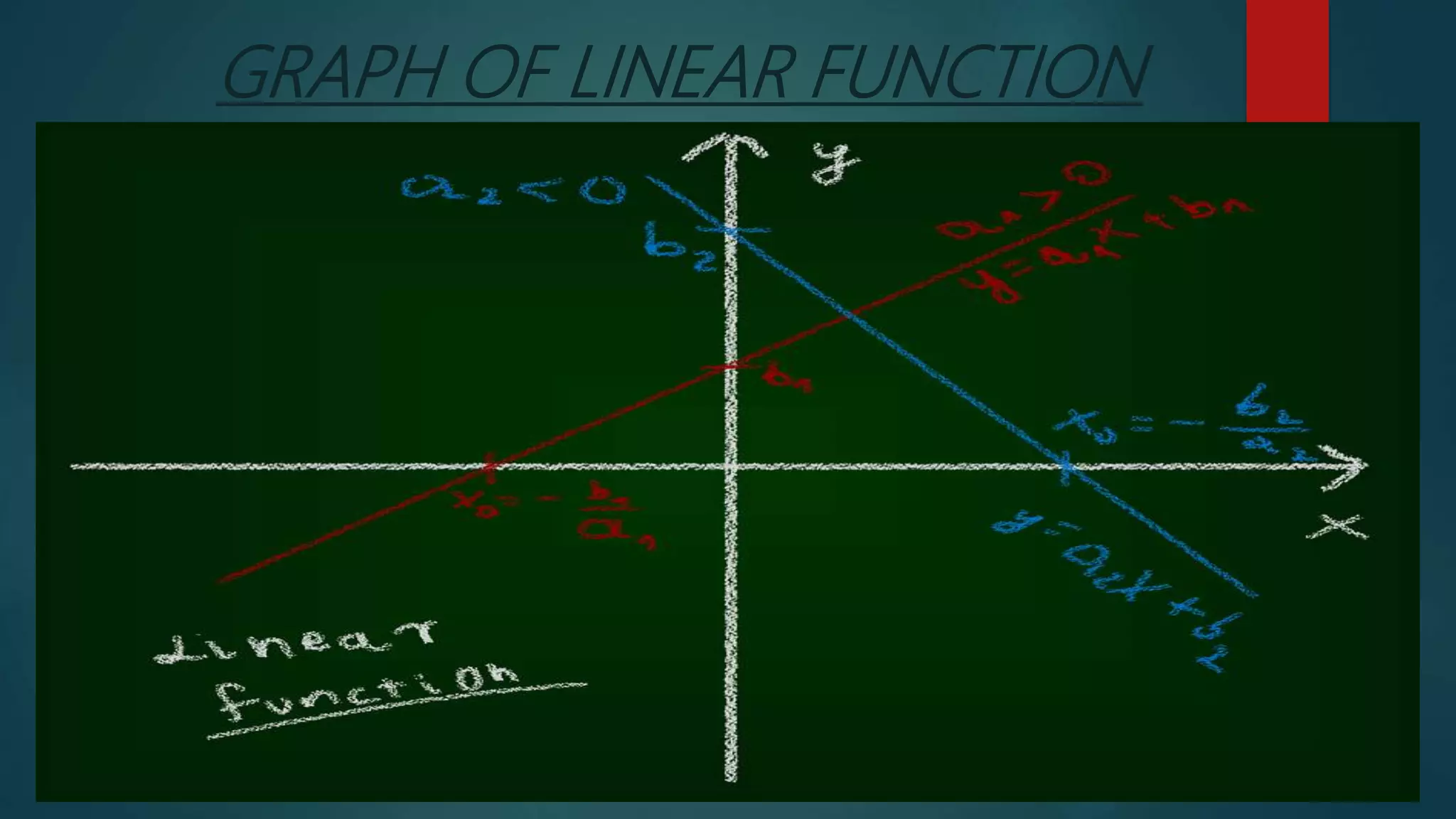
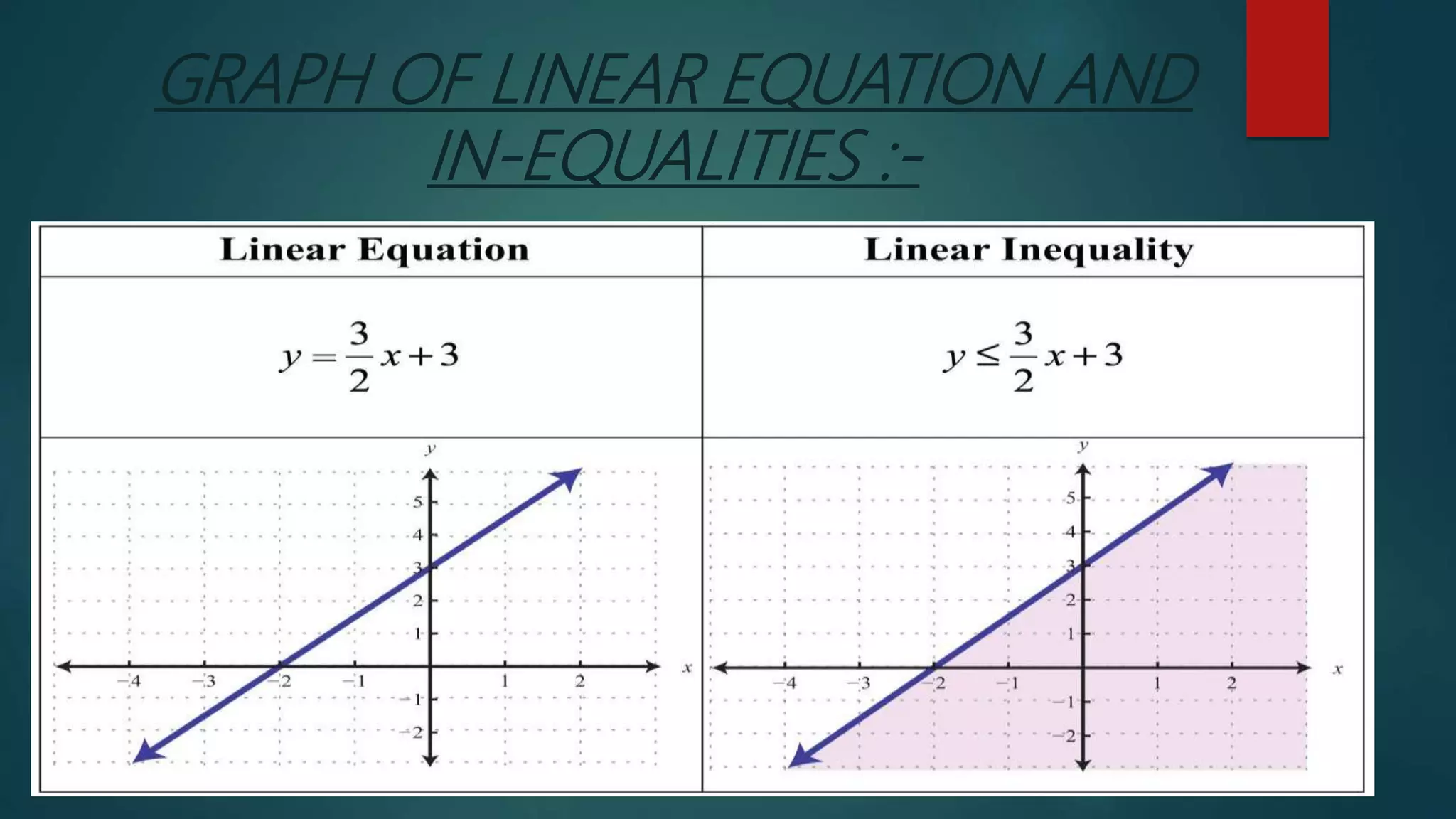
The document provides information about linear equations and functions. It includes: 1. A list of 5 students with identification numbers. 2. An overview of topics to be covered related to linear equations and functions, including solving linear equations and inequalities, functions, linear functions, and systems of linear equations. 3. Details on solving linear equations and inequalities in one variable, including examples and properties. 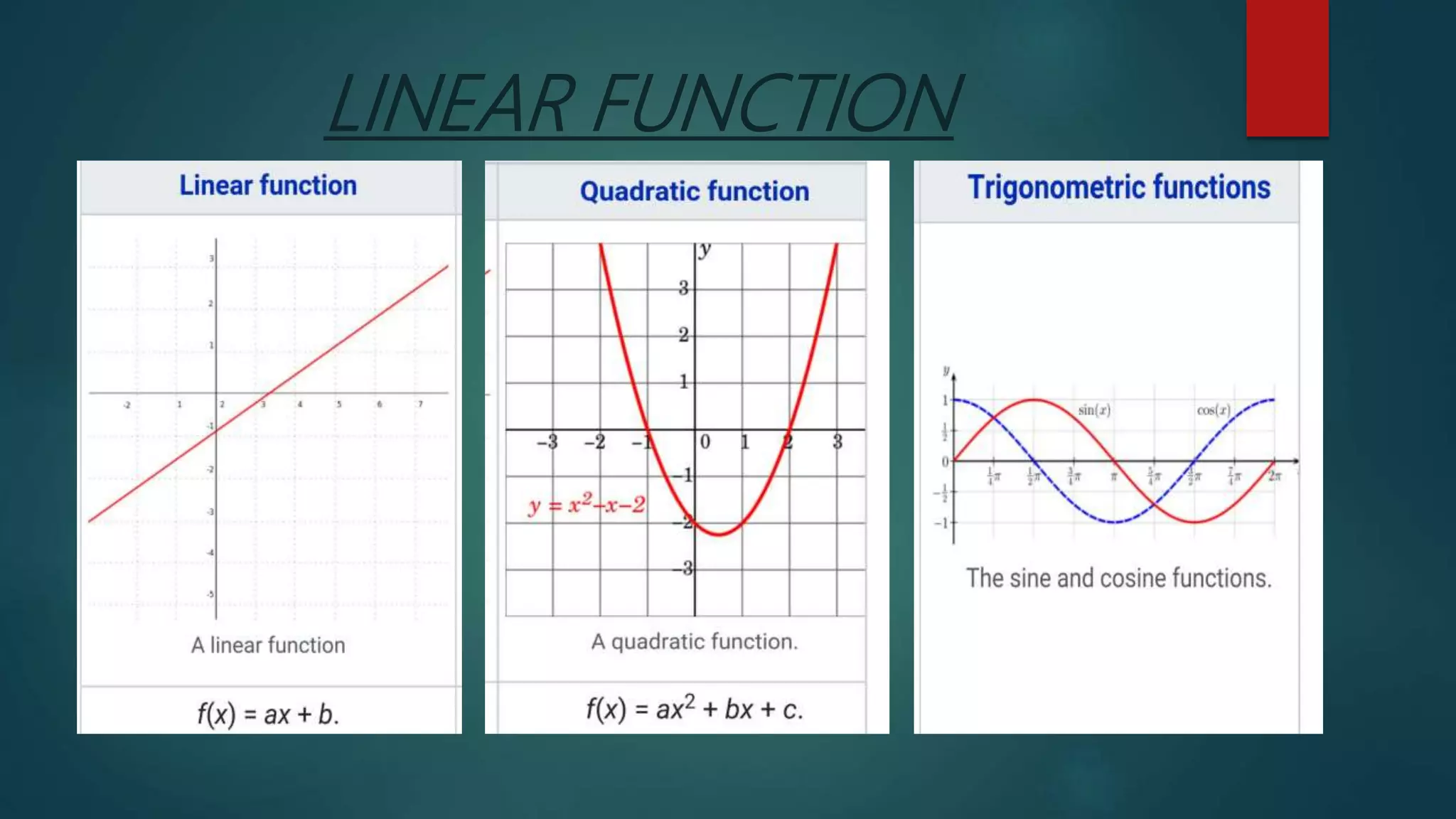4. Information on different types of functions, including algebraic, trigonometric, exponential, and logarithmic functions. 5. Examples of using linear functions in business and economics, such as profit functions, break-even points, supply and demand curves.

2. FABULOUS FIVE
0017 Rija Arshad
0030 Sania Ijaz
0031 Anam Zahid
0048 Alisha Asghar
0141 Sidra Basharat

3. LINEAR EQUATIONS AND
FUNCTIONS
 Solution of Linear Equation & Inequalities in one
variable.
 Functions , notation operation with function.
 Linear function graph, slopes, equations.
 Solution of system of linear equations in three
variables.
 Applications of functions in business and
economics.

4. SOLUTION OF LINEAR EQUATIONS
& INEQUALITIES IN ONE VARIABLE
INTRODUCTION
 Linear equations were
invented in 1843 by Irish
mathematician Sir William
Rowan Hamilton. He was born
in 1805 and died in 1865. Sir
Hamilton made important
contributions to mathematics.

5. DIFFERENTIATE BETWEEN
EQUALITY & IN-EQUALITY
EQUATION:-
An equation is a mathematical
statement wherein two expressions are
set equal to each other.
FOR EXAMPLE:-
𝟐
𝟑
𝒙 −
𝟏
𝟐
𝒙 = 𝒙 +
𝟏
𝟔
IN-EQUALITY:-
A Formal statement of inequality
between two quantities usually
separated by a sign of inequality (as < ,
> or ≠ OR signifying respectively is less
than, is greater than, or is not equal to).
FOR EXAMPLE:-
𝟑𝒙 + 𝟏 < 𝟓𝒙 − 𝟒
𝟗 − 𝟕𝒙 > 𝟏𝟗 − 𝟐𝒙

6. PROPERTIES OF EQUALITY
ADDITION
PROPERTY
The equation formed by
adding the same quantity to
both side of an equation is
equivalent to the original
equation.
Example:-
𝒙 − 𝟒 = 𝟔 is equivalent to
𝒙 = 𝟏𝟎
SUBSTITUTION
PROPERTY
The equation formed by
substituting one expression for
an equal expression is
equivalent to original
equation.
Example:-
𝟑 𝒙 − 𝟑 −
𝟏
𝟐
𝟒𝒙 − 𝟏𝟖 = 𝟒
Is equivalent to
𝟑𝒙 − 𝟗 − 𝟐𝒙 + 𝟗 = 𝟒 & 𝒕𝒐 𝒙 = 𝟒
The solution set is {4}
MULTIPLICATION
PROPERTY
The equation forms by multiplying
both side of an equation by the same
non zero quantity is equivalent to the
original equation.
Example:-
𝟏
𝟑
𝒙 = 𝟔 𝑖𝑠 𝑒𝑞𝑢𝑖𝑣𝑎𝑙𝑒𝑛𝑡 𝑡𝑜 𝟑
𝟏
𝟑
𝒙
= 𝟑 𝟔 𝒐𝒓 𝒕𝒐 𝒙 = 𝟏𝟖

7. TO SOLVE LINEAR EQUATION IN ONE
VARIABLE
1. SIMPLIFY BOTH SIDE OF EQUATION.
2. USE THE ADDITION AND SUBSTRACTION
PROPERTY.
3. SIMPLIFY BOTH SIDE OF THE EQUATIONS.
4. DIVIDE BOTH SIDE OF THE EQUATION BY THE
COEFFICIENT OF THE VARIABLE.

8. EXAMPLE:-
 SOLVE:-
𝑥 + 1 = 3 𝑥 − 5
𝑥 + 1 = 3 𝑥 − 5 (Original equation)
𝑥 + 1 = 3𝑥 − 15 (simplify right hand side)
𝑥 = 3𝑥 − 15 − 1
𝑥 = 3𝑥 − 16 (by subtracting 1 from 16)
−2𝑥 = −16 (by subtracting 1 from 3x)
𝑥 = −
16
−2
𝒙 = 𝟏𝟖 (by dividing -2)
The solution is 8
Check :- 8+1=3(8-5)
9=3(3)
9=9

9. SOLUTION OF LINEAR EQUATION
FUTURE VALUE OF AN INVESTMENT :-
The future value of a simple interest investment is given by S= p+ prt ,where p is the principal invested, r is the
annual interest rate (as a decimal), and t is the time in years, at what simple interest r must p=1500 dollars be
invested so that the future value is $2940 after 8 year.
Solution:-
Entering the values S=2904, P=1500, and t into S=P +prt gives
2940 = 1500 + 1500(r)(8)
2940=1500+12,000r
2940-1500=12,000r
1440=12,000r
1440/12,000 = r
0.12 = r
So, the interest rate is 0.12 or 12 % .

10. SOLUTION OF LINEAR EQUATION :-
VOTING
Example:- Using data from 1952-2004, the percent p of the eligible U.S. population voting is
presidential selection has been estimated to be
p=63.20 – 0.26x
Where x is the number of years past 1950. according to this model/ in what election year is the %
voting equal to 55.4% ?
Solution:-
55.4=63.20 – 0.26x
-7.8= - 0.26x
30=x

11. SOLVING OF LINEAR EQUATION
PROFIT :-
SUPPOSE THAT THE RELATIONSHIP BETWEEN A FIRM’S PROFIT P AND THE
NUMBER X OF ITEM SOLD CAN BE DESCRIBED BY THE EQUATION.
5x – 4p = 1200
Find the profit when 240 units are sold.
when, p =
𝟓
𝟒
𝒙 − 𝟑𝟎𝟎
=
𝟓
𝟒
𝟐𝟒𝟎 − 𝟑𝟎𝟎
p = 0
It means profit is zero when the firm produced 240 units.

12. SOLVING OF LINEAR IN-EQUALIIES IN
ONE VARIABLE :-
DEFINITION :-
A linear inequality in one variable is a sentence of the form ax + b < 0 , a 6= 0.
EXAMPLE :-
Solve x + 2 < 4
x + 2 < 4
x < 4 – 2
x < 2
The graph of this solution is as follow:-
-1 0 1 2 3 5

13. GRAPH OF LINEAR EQUATION AND
IN-EQUALITIES :-

14. FUNCTION
 It is a relationship between a set of inputs and a set of outputs with the
property that each input related to exactly that output
Example:-
A depend on “X” where A is the area and formula is
A =𝑥2
, here A is a function of x
If Y depends on x then Y is a function of x
y= f(x)

15. TYPES OF FUNCTIONS
1- Algebraic function
 polynomial function
 linear function
 quadratic function
 identity function
 constant function
 rational function
2- Trigonometric function
3- Inverse trigonometric function
4- Exponential function
5- Logarithm function

16. LINEAR FUNCTION

17. EXAMPLE:-
 The total cost of producing a product is given by
C(x)=300x+0.1𝑥2+1200
Where x represents the number of unit produced.
Find the total cost of producing 10 units:-
x=10
C(x)=300x+0.1𝑥2
+1200
C(10)=300(10)+0.1(10)2+1200
C(10)=3000+10+1200
C(10)=4210
when we’ll produce 10 units the total cost will be 4210

18. APPLICATION OF FUNCTION IN
DAILY LIFE
MONEY AS A FUNCTION OF TIME.
YOU NEVER HAVE MORE THEN ONE
AMOUNT OF MONEY AT ANY TIME
BECAUSE YOU CAN ALWAYS ADD
EVERYTHING TO GIVE ONE TOTAL
AMOUNT BY UNDERSTANDING HOW
YOUR MONEY CHANGES OVER TIME,
YOU CAN PLAN TO SPEND YOUR
MONEY SENSIBLY.

19. LINEAR FUNCTION
 A linear function involves a record variable like y , and a variable like x
whose highest power is 1.
EXAMPLE:-
Y=2X+4
Y=5X+25
Y=3X+12

20. LINEAR FUNCTION
DOMAIN
 All the x-coordinates in the function’s
ordered pairs
Example:-
{3.2.5}
RANGE
 All the y-coordinates in the function’s
ordered pair
Example:-
{6,8,3}

21. GRAPH OF LINEAR FUNCTION

22. EXAMPLE:-
Depreciation:-
A business property is purchased for $ 122,880 and depreciated over a its value y is related to the
number of months of service x by the equation
 𝟒𝟎𝟗𝟔𝒙 + 𝟒𝒚 = 𝟒𝟗𝟏520
Find the x-intercept and the y-intercept and use them to sketch the graph
Solution:-
for x-intercept , y=0 gives 4096𝑥 = 491,520
𝐱 = 𝟏𝟐𝟎
Thus 120 is the x-intercept
for y-intercept , x=0 gives 4𝑦 = 491,520
𝒚 = 𝟏𝟐𝟐, 𝟖𝟖𝟎
Thus 122,880 is the y-intercept

23. LINEAR FUNCTION EXAMPLE IN REAL LIFE

24. ‘’APPLICATION OF FUNCTIONS IN
BUSINESS AND ECONOMICS’’
Here are some applications of Functions:
 Profit & Break-Even Point
 Supply, Demand & Market Equilibrium
1. Profit Function:
The profit is the net proceeds, or what remains the revenue
when costs are subtracted.
Profit= revenue-cost

25. EXAMPLE OF PROFIT FUNCTION:
Suppose that profit function for a product is linear and marginal profit is $5. if
the profit is $200 when 125 units are sold, write the equation of the profit
function.
Solution:
The marginal profit gives us the slope of the line representing the profit
function. Using this slope(m=5) and the point(125,000) in the point-slope
formula P-P1=m(x-x1) gives
P-200=5(x-125)
or
P=5x-425

26. 2. BREAK-EVEN POINT:
In break-even point is the number of item x at which break-even occurs.
In break-even point revenue is equal to cost.
Formula:
Revenue=Cost
In Break-Even point PROFIT = ZERO
LOSS = ZERO
EXAMPLE:-
4P=81x-29970
4(0)=81x-29970
29970=81x
29970/81=x
x=370.

27. 3. SUPPLY & DEMAND:
Supply:
 The law of Supple states that the quantity
supplied for sale will increase as the prices of
the product increase.
Demand:
 The law of Demand states that the quantity
demanded increases as the prices decreases and
vise versa.

28. EXAMPLE OF DEMAND AND
SUPPLY IN DAILY LIFE

29. 4. MARKET EQUILIBRIUM:
 IN market-equilibrium supply is equal to demand.
Market equilibrium occurs when the quantity of a commodity demanded is equal to the
quantity supplied.
Example:
Find the equilibrium point for the following supply and demand function.
Demand: p= -3q+36
Supply: p=4q+1
At market equilibrium, the demand price equals the supply price. Thus,
demand=supply
-3q+36=4q+1
35=7q
35/7=q q=5
Putting the value of q in equation 2 , you’ll find the value of P=21
q=5
p=21
So the market-equilibrium point is (5,21)

30. ‘’SOLUTION OF SYSTEM OF LINEAR
EQUATION’’
 It is a collection of 2 or more linear
equation involving same set of
variables that you deal all together
at once.
For Example:
x+2y=4
3x+5y=7

31. METHODS OF SOLUTION OF
SYSTEM OF LINEAR EQUATION
 There are 2 methods of solving of
system of linear equation:
 Elimination Method.
 Substitution Method.

32. SUBSTITUTION METHOD
NO SOLUTION
-4x+8y=9
x-2y=3
By multiplying equation 2 with 4
4(x-2y)=4(3)
4x-8y=12
-4x+8y=9
4x-8y=12
0x+0y=21
0=21 NO SOLUTION
SOLUTION
5x+4y=1
3x-6y=2
By multiplying equation 1 with 3
By multiplying equation 2 with 2
3(5x+4y)=3(1), 2(3x-6y)=2(2)
15x+12y=3 (eq 3) , 6x-12y=4 (eq 4)
By adding equation 3 and 4
15x+12y=3
6x-12y=7
21x =7 x=7/21 x=1/3
By putting the value in equation 2
3(1/3)-6y=2
1-6y=2
Y= -1/6

33. Elimination Method
Example:
x + y=335
10x+7y=2741
Solution:
multiplying equation 1 with -10.
-10(x + y)=335(-10)
-10x-10y=-3350
-10x-10y=-3350
10x+7y=2741
-3y=-609 y=-609/3 y=203
Applying the value of y in equation 1.
X+203=335
x=335-203
x=132

34. EXAMPLE OF SYSTEM OF LINEAR
EQUATION IN REAL LIFE

35. EXAMPLE OF SYSTEM OF LINEAR
EQUATION:-