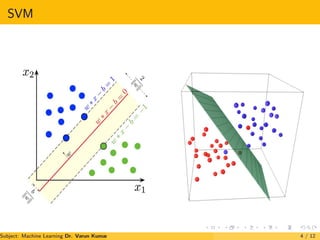
1. Support vector machine is a supervised machine learning algorithm that constructs a hyperplane or set of hyperplanes to classify data points. 2. It finds the optimal hyperplane that separates classes of data points by maximizing the margin between the closest data points of each class. 3. The optimal hyperplane is the one that maximizes the margin of separation between the different classes and minimizes the risk of misclassifying new data points.

1. Support Vector Machine
Subject: Machine Learning
Dr. Varun Kumar
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 1 / 12

2. Outlines
1 Introduction to Support Vector Machine (SVM)
2 Linearly vs Non-linearly Separable Pattern/Class
3 Mathematical Intuition for Hyperplane
4 Support Vector and Optimal Hyperplane
5 References
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 2 / 12

3. Introduction to support vector machine (SVM):
Key Features:
1 Support vector machine is a tool under supervise learning.
2 It is binary classifier.
3 Support vector machine constructs a hyperplane as the decision
surface in such a way that the margin of separation between positive
and negative examples.
Q What is hyperplane ?
Q What is decision surface ?
Q What is margin of separation ?
Q What is positive and negative example ?
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 3 / 12

4. SVM
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 4 / 12

5. Linearly vs non-linearly separable pattern/class
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 5 / 12

6. Mathematical intuition for optimal hyperplane
Optimal hyperplane for linearly separable pattern
⇒ Consider the training sample {(xi , di )}N
i=1
⇒ xi is the input pattern for the ith example.
⇒ di → Corresponding desired response (target output).
⇒ Initial assumption → Class di = 1 and di = −1 are linearly separable.
⇒ The equation for decision surface is
wT
x + b = 0 (1)
x is an input vector, w is an adjustable weight vector, and b is a bias.
wT
x + b ≥ 0 ⇒ di = +1
wT
x + b < 0 ⇒ di = −1
(2)
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 6 / 12

7. Support vector and optimal hyperplane
⇒ Closest data point is called the margin of separation or support
vector and it is denoted by ρ.
⇒ SVM find the particular hyperplane for which the margin of
separation ρ is maximized.
⇒ Let ρ0 = max{ρ} then that hyperplane is called the optimal
hyperplane.
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 7 / 12

8. Optimal hyperplane
⇒ Let w0 and b0 denotes the optimum value of the weight vector and
bias.
⇒ Optimal hyperplane represents a multidimensional linear decision
surface in the input space is
wT
0 x + b0 = 0 (3)
Let the discriminant function is
g(x) = wT
0 x + b0 (4)
⇒ Discriminant function gives an algebraic measure of the distance from
x to the optimal hyperplane.
⇒ The easiest way for expressing the input vector x
x = xp + r
w0
k w0 k
(5)
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 8 / 12

9. Continued–
⇒ xp is the normal projection of x onto the optimal hyperplane.
⇒ r is the desired algebraic distance.
⇒ If r is +ve, x is on the +ve side of the optimal hyperplane and
vice-versa.
⇒ By definition g(xp) = 0 and g(x) = wT
0 x + b0 = rk w0 k. Hence,
r =
g(x)
k w0 k
(6)
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 9 / 12

10. Important observation
1 The distance from origin (i.e, x=0) to the hyperplane is b0
kw0k
2 If b0 > 0 → The origin is on the +ve side of hyperplane or vice-versa.
3 If b0 = 0 → The optimal hyperplane passes through the origin.
4 Let a training set T = {(xi , di )}, we observe that the pair (w0, b0)
satisfy the following constraints
wT
0 xi + b0 ≥ 1 ⇒ di = +1
wT
0 xi + b0 < 1 ⇒ di = −1
(7)
5 Consider a support vector x(s) for which d(s) = +1 then by definition,
we have
g(x(s)
) = wT
0 x
(s)
+ b0 = ±1 ⇒ di = ±1 (8)
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 10 / 12

11. Continued–
6 The algebraic distance from the support vector x(s) to the optimal
hyperplane is
r =
g(x(s))
k w0 k
1
k w0 k
⇒ if d(s)
= +1
−1
k w0 k
⇒ if d(s)
= −1
(9)
7 Let ρ denotes the optimum value of margin between two classes that
constitutes the training sample T , then
ρ =2r =
2
k w0 k
(10)
8 Maximizing the margin of separation is equivalent to minimizing the
Euclidean norm of the weight vector w
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 11 / 12

12. References
E. Alpaydin, Introduction to machine learning. MIT press, 2020.
J. Grus, Data science from scratch: first principles with python. O’Reilly Media,
2019.
T. M. Mitchell, The discipline of machine learning. Carnegie Mellon University,
School of Computer Science, Machine Learning , 2006, vol. 9.
Subject: Machine Learning Dr. Varun Kumar (IIIT Surat) 12 / 12