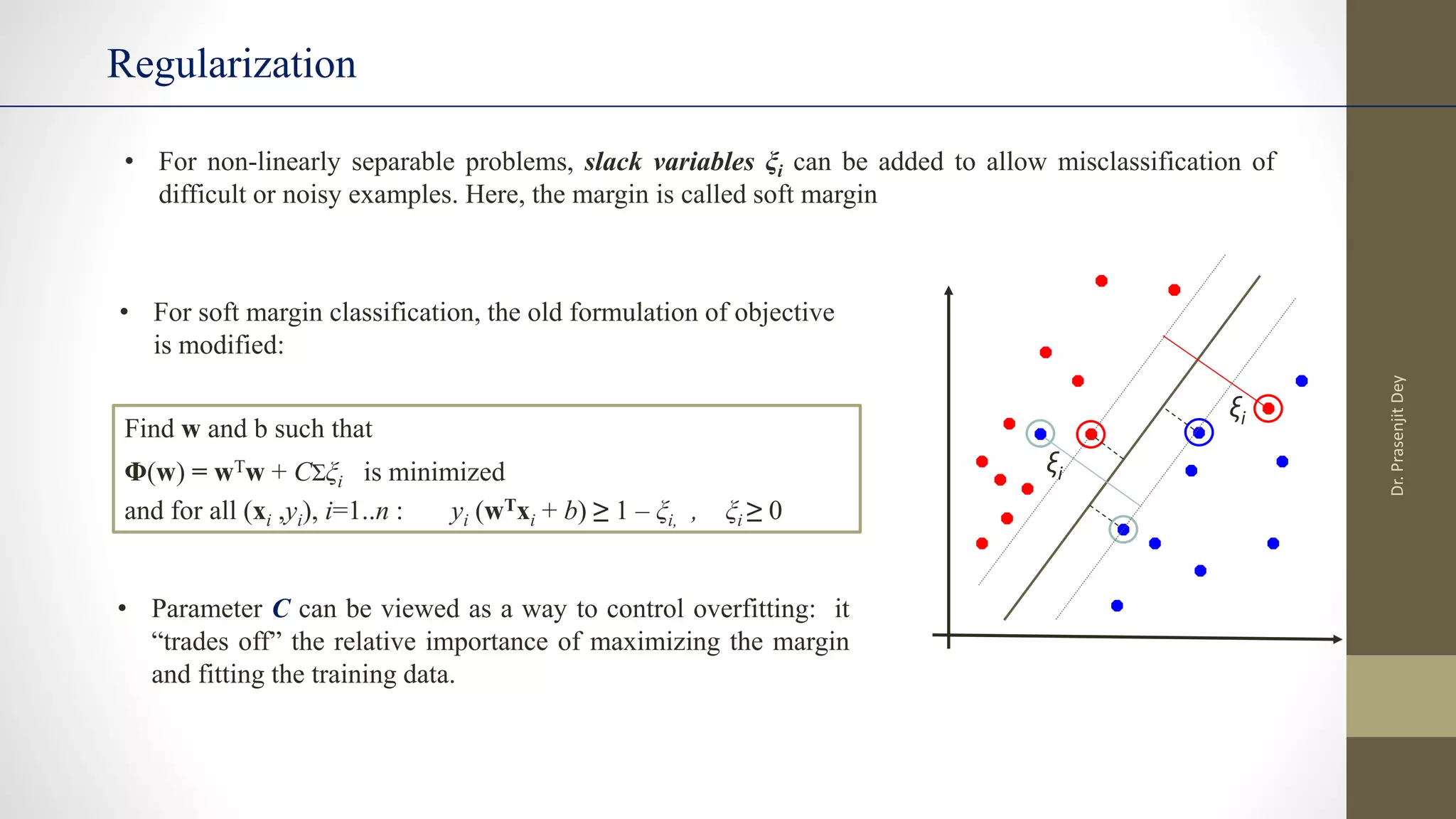
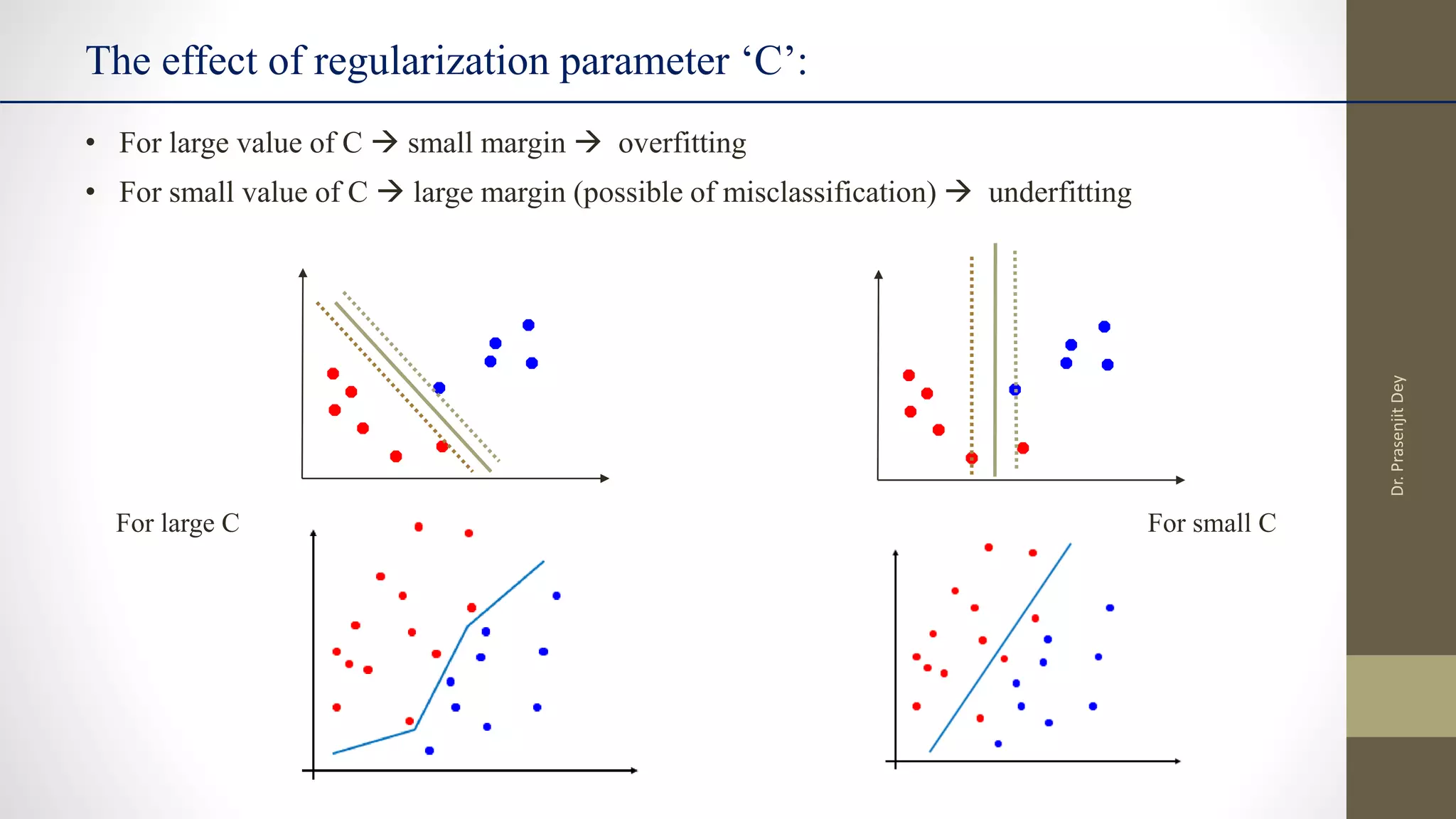
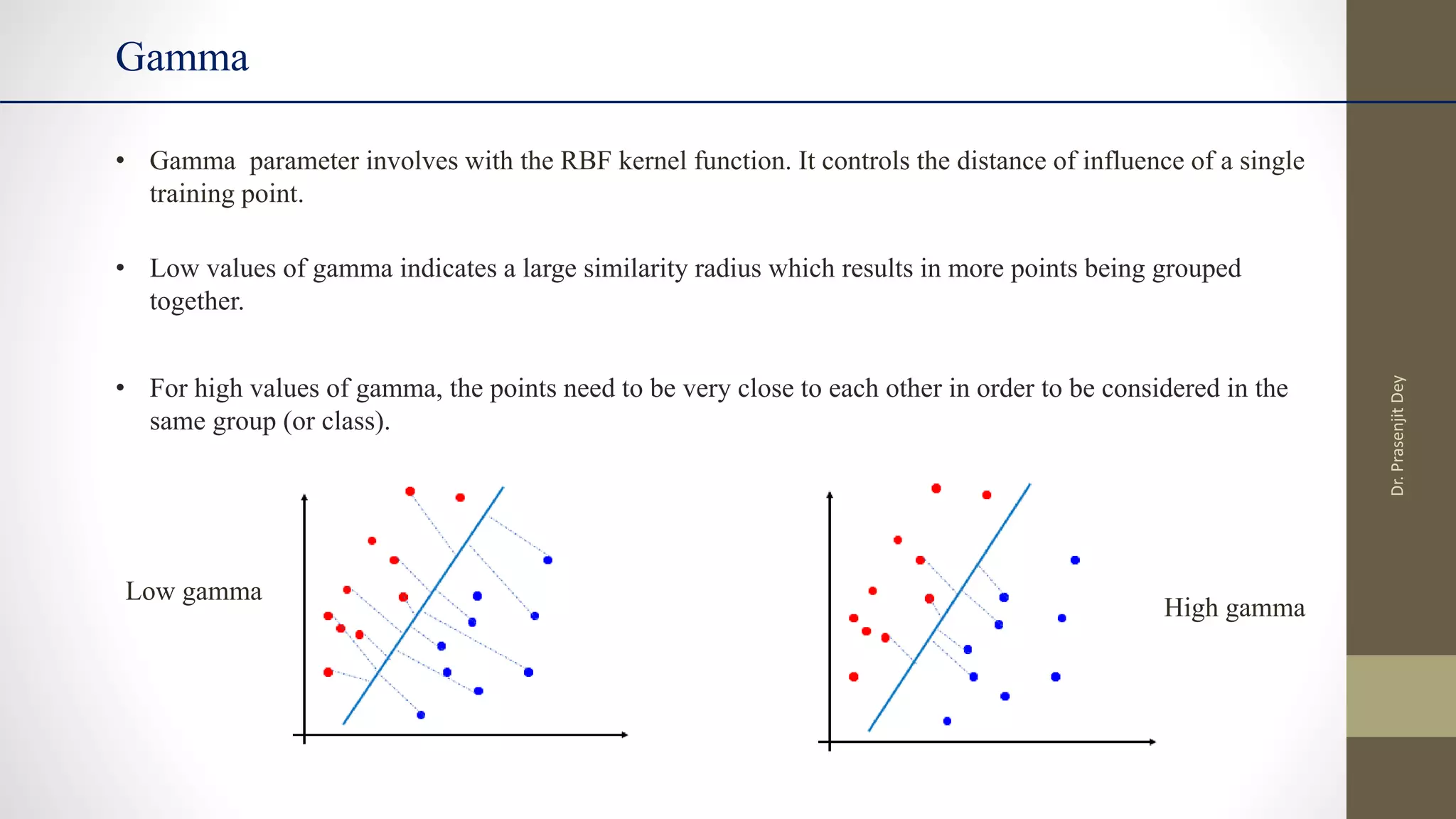
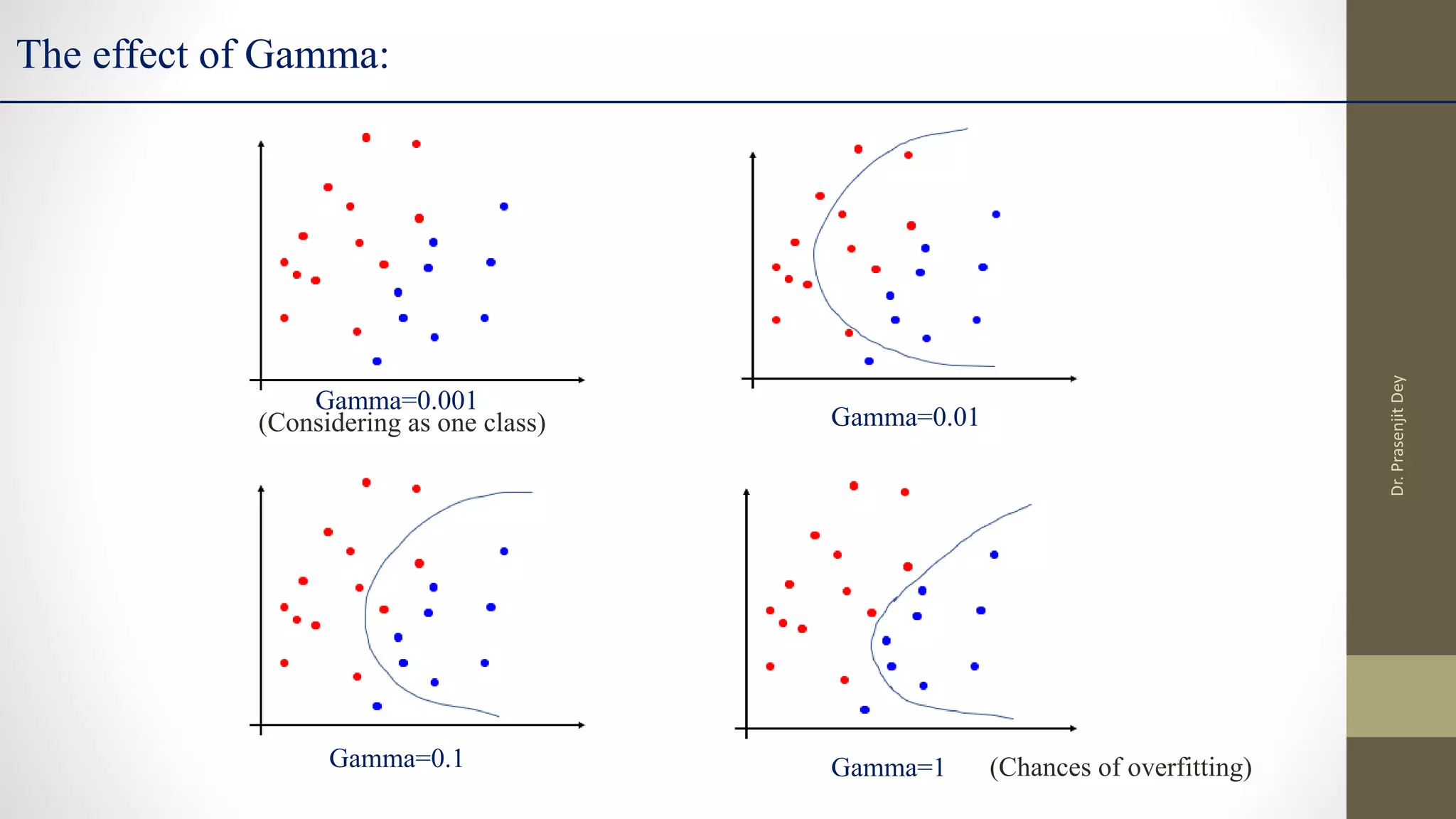
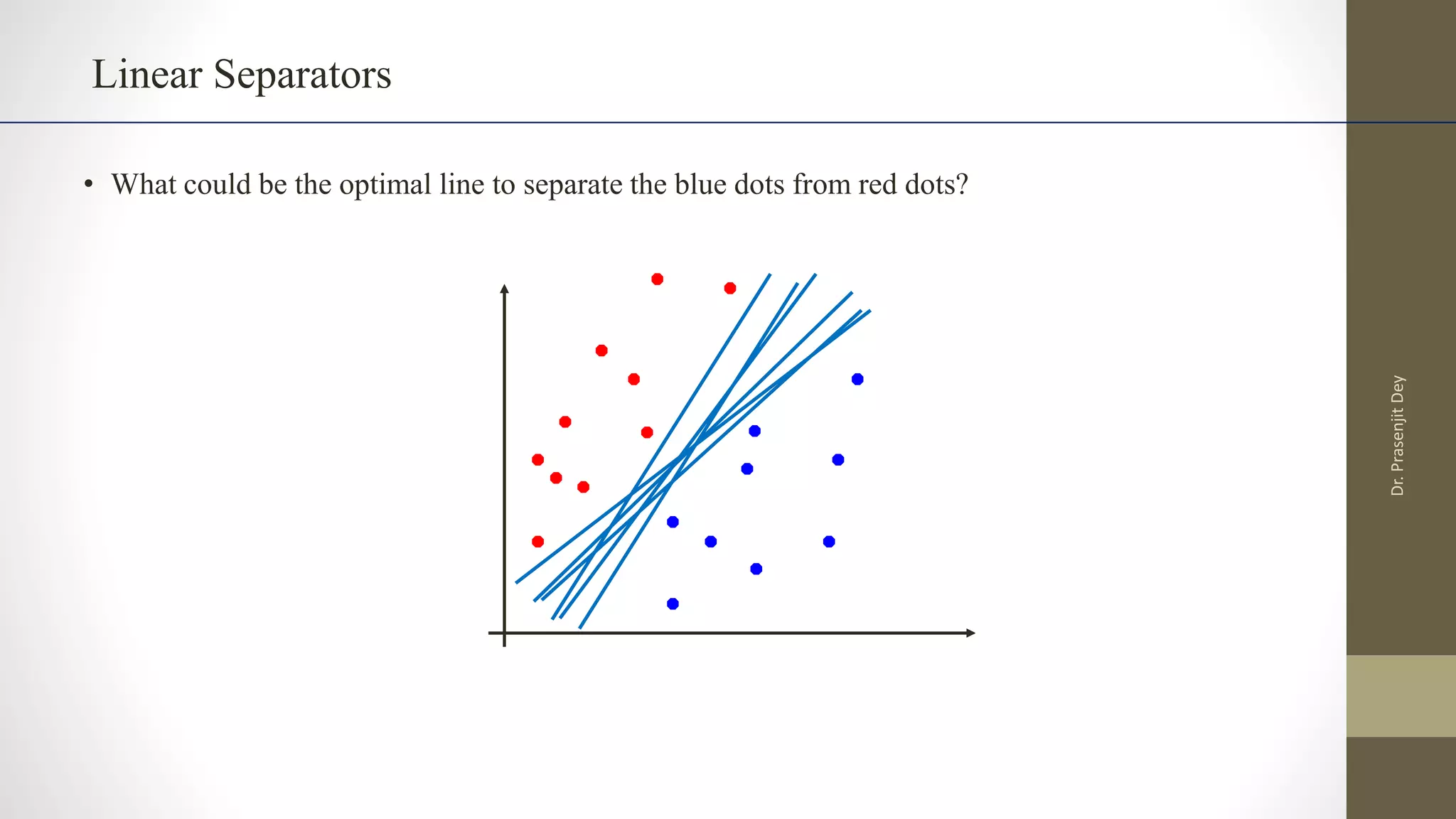
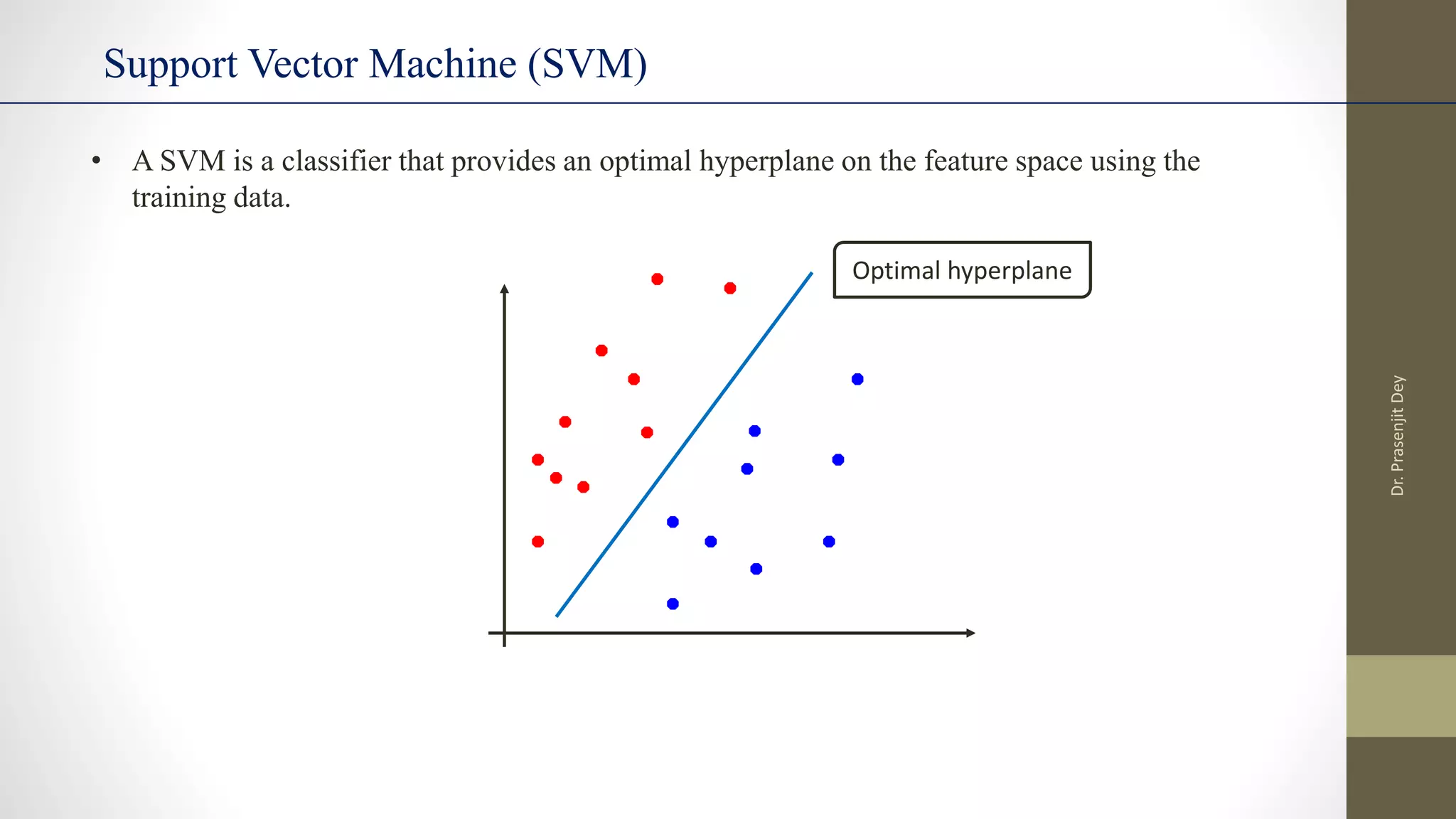
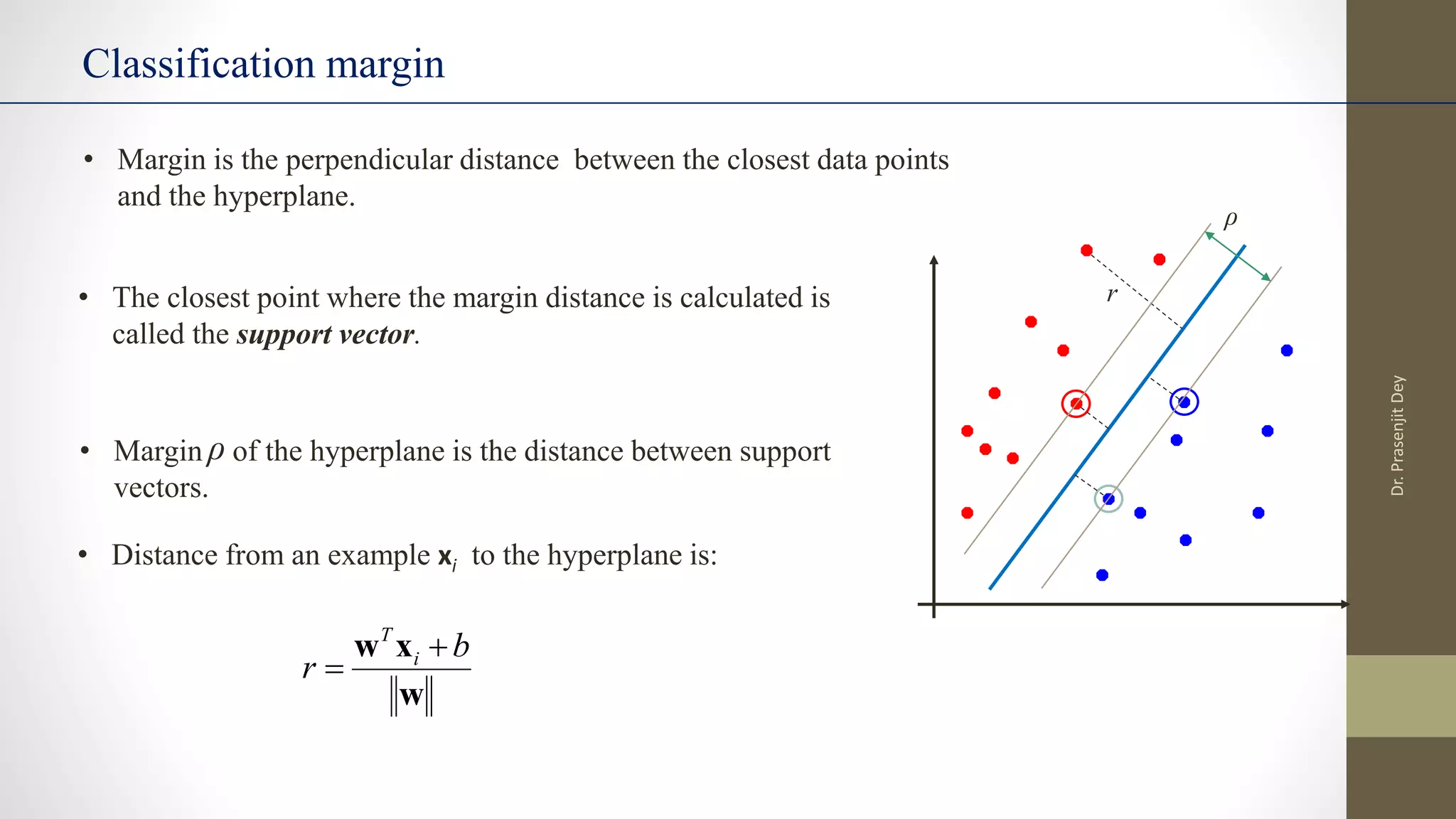
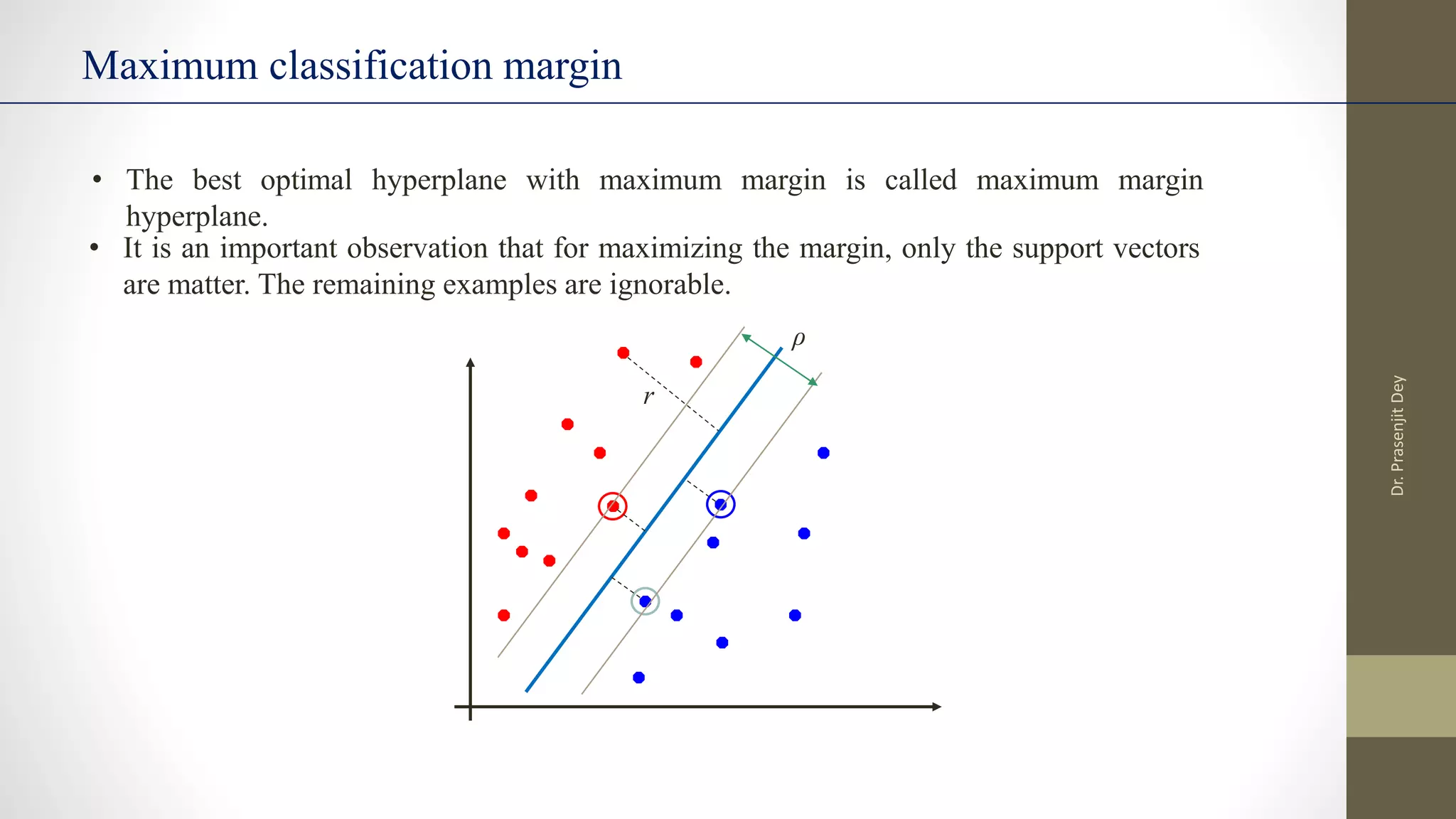
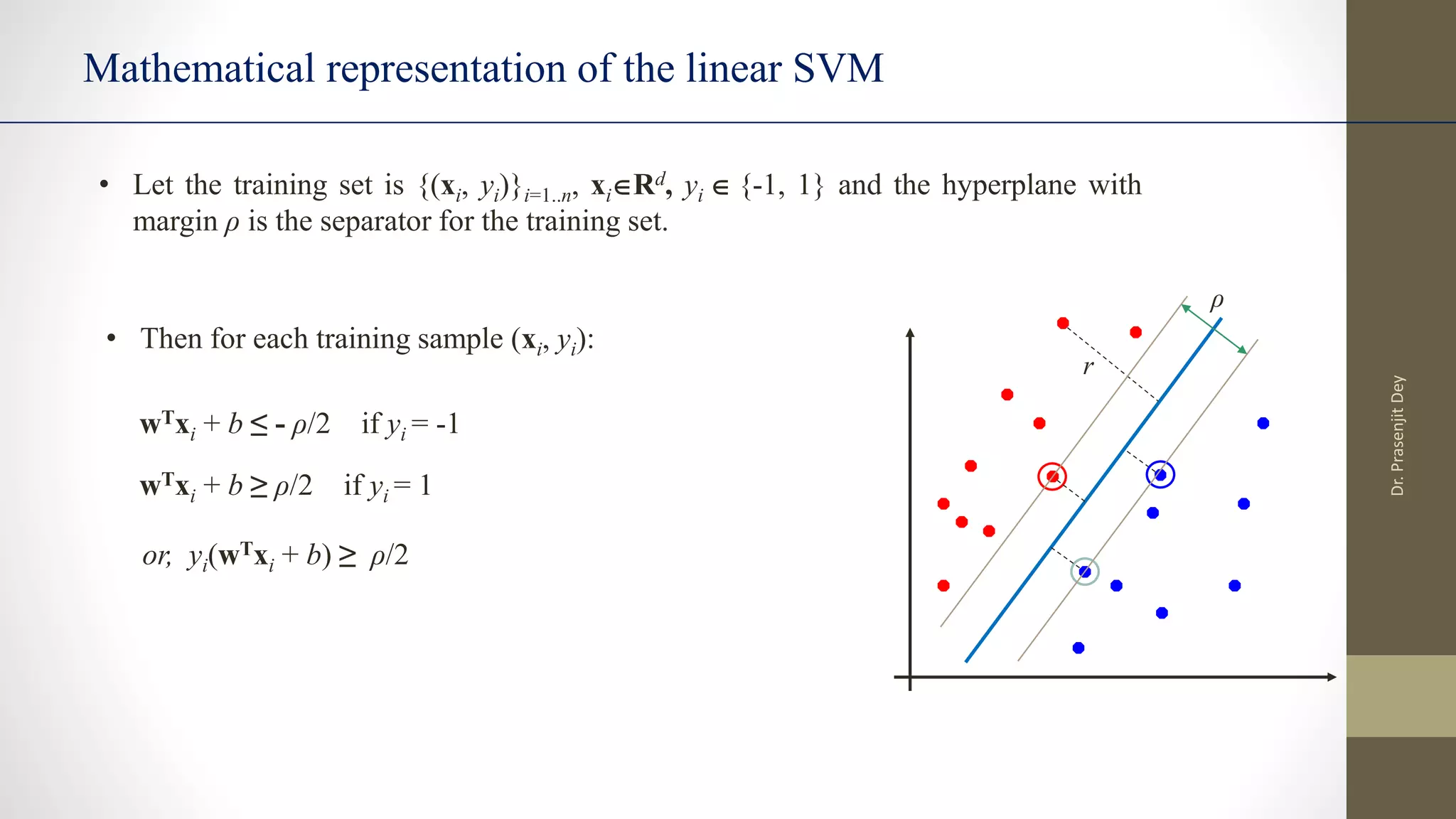
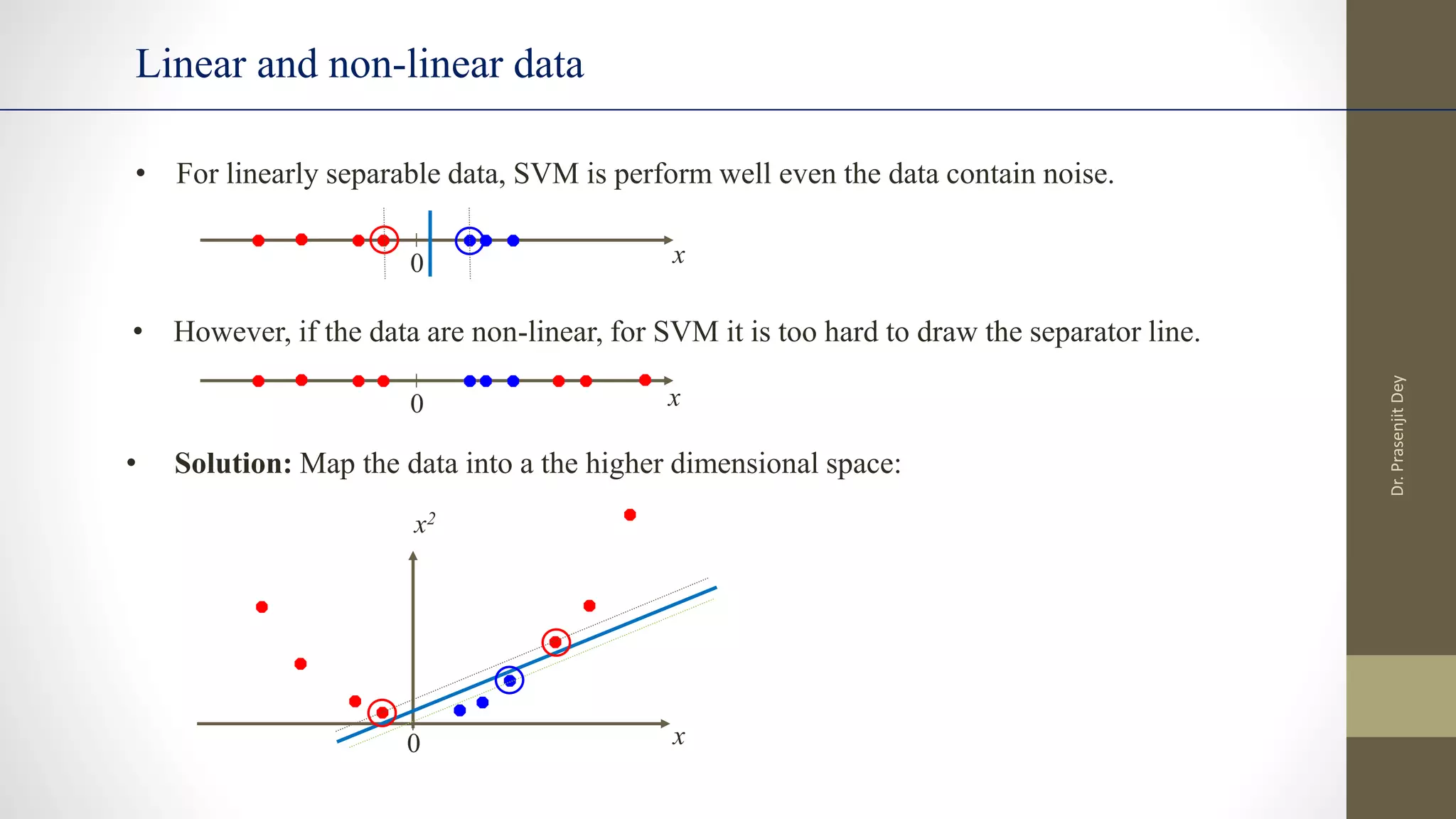
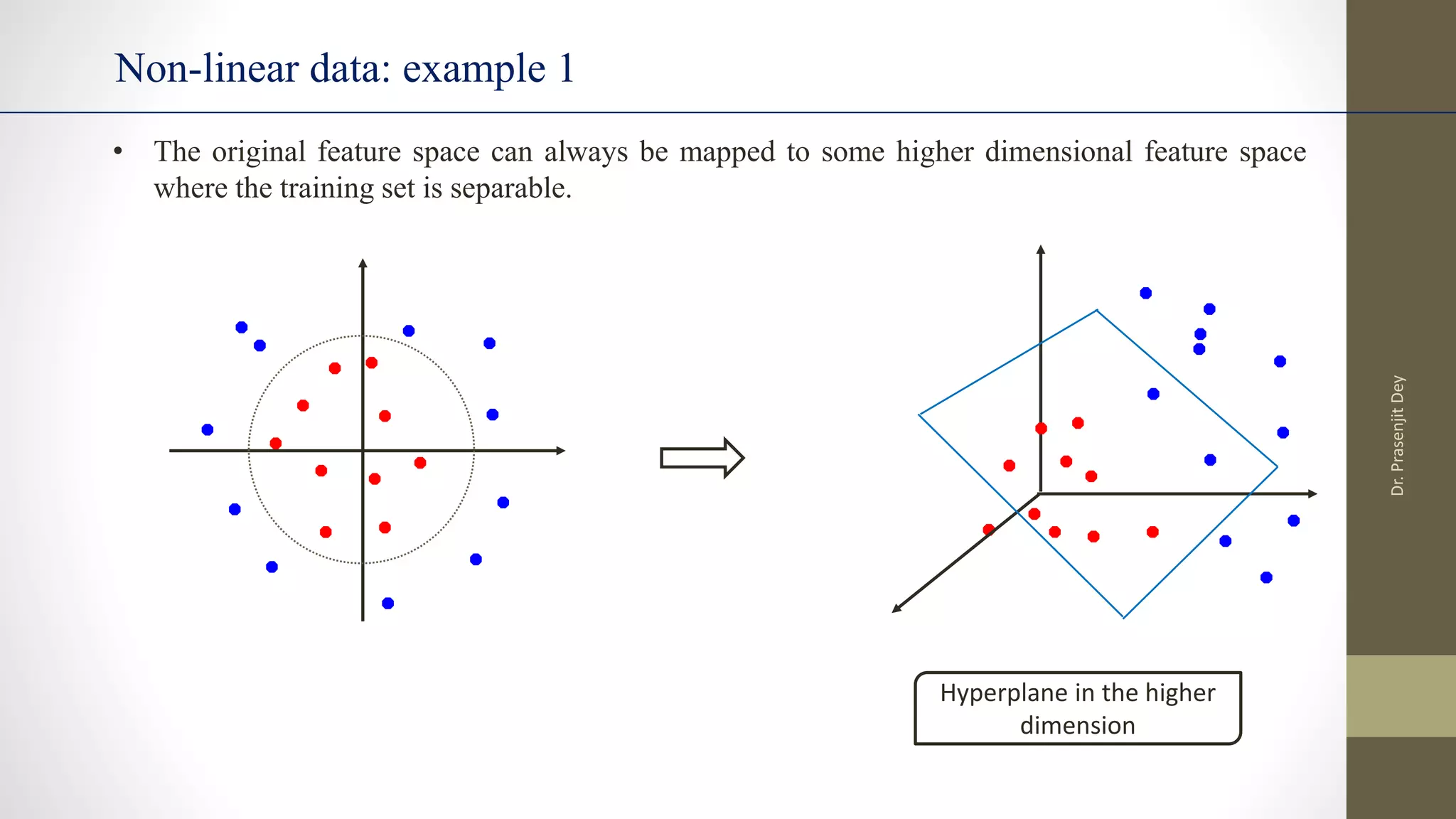
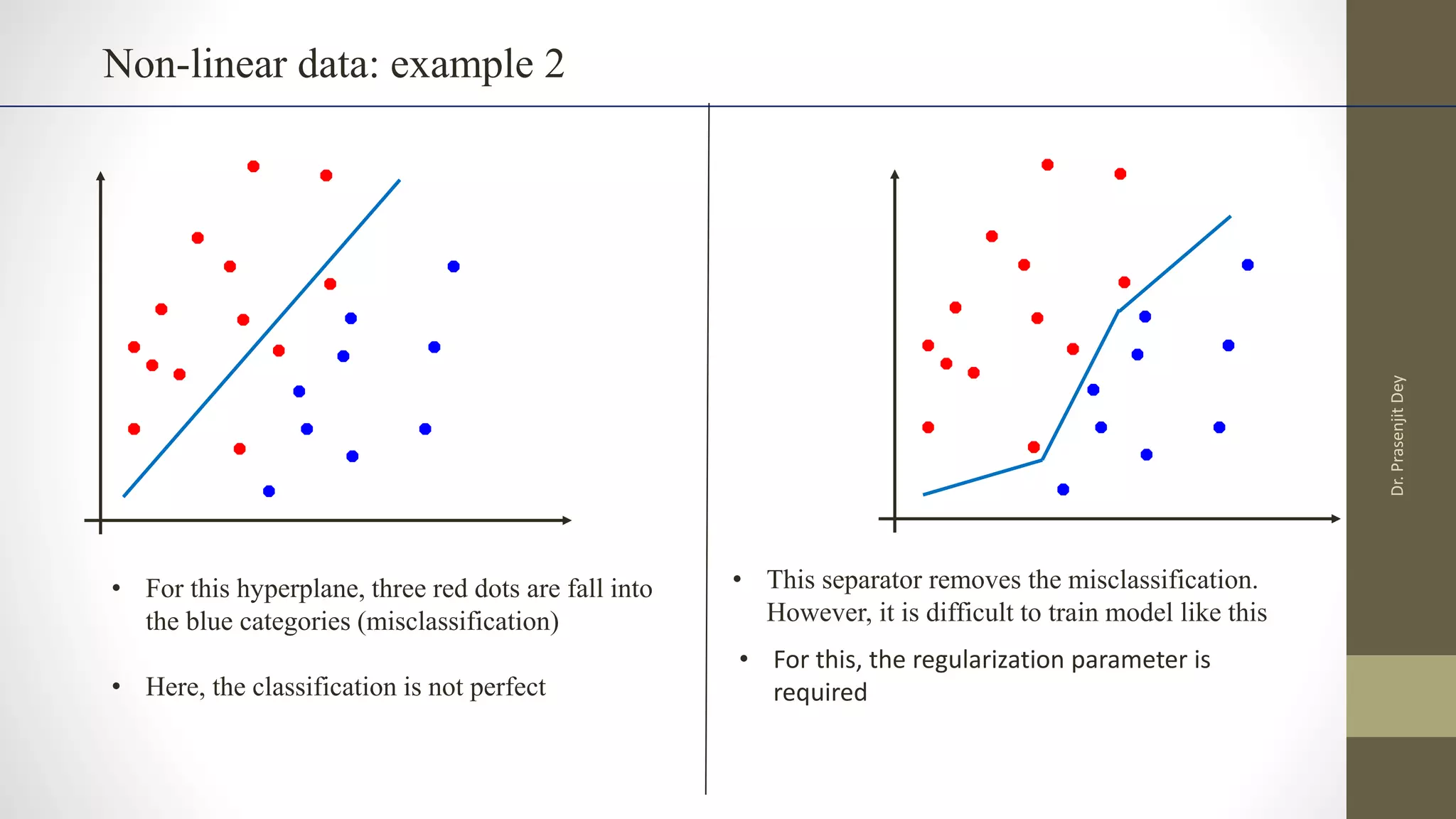
The document discusses support vector machines (SVMs). SVMs find the optimal separating hyperplane between classes that maximizes the margin between them. They can handle nonlinear data using kernels to map the data into higher dimensions where a linear separator may exist. Key aspects include defining the maximum margin hyperplane, using regularization and slack variables to deal with misclassified examples, and kernels which implicitly map data into other feature spaces without explicitly computing the transformations. The regularization and gamma parameters affect model complexity, with regularization controlling overfitting and gamma influencing the similarity between points.

1. Support Vector Machine (SVM)
Dr. Prasenjit Dey
Dr.
Prasenjit
Dey

2. Linear Separators
• What could be the optimal line to separate the blue dots from red dots?
Dr.
Prasenjit
Dey

3. Support Vector Machine (SVM)
• A SVM is a classifier that provides an optimal hyperplane on the feature space using the
training data.
Optimal hyperplane
Dr.
Prasenjit
Dey

4. Classification margin
w
x
w b
r i
T


r
ρ
• Margin is the perpendicular distance between the closest data points
and the hyperplane.
• The closest point where the margin distance is calculated is
called the support vector.
• Margin of the hyperplane is the distance between support
vectors.
• Distance from an example xi to the hyperplane is:
ρ
Dr.
Prasenjit
Dey

5. Maximum classification margin
• The best optimal hyperplane with maximum margin is called maximum margin
hyperplane.
• It is an important observation that for maximizing the margin, only the support vectors
are matter. The remaining examples are ignorable.
r
ρ
Dr.
Prasenjit
Dey

6. Mathematical representation of the linear SVM (contd.)
• For every support vector xs , the above inequality is an equality. After rescaling w and b
by ρ/2 in the equality, we obtain that distance between each xs and the hyperplane is
w
2
2 
 r

• Then the margin can be expressed through (rescaled) w and b as:
• Objective is to find w and b such that is maximized and
for all (xi, yi), i=1..n : yi(wTxi + b) ≥ 1
w
2


w
w
x
w 1
)
(
y



b
r s
T
s
• The objective can be reformulated as: find w and b such that Φ(w) = ||w||2= wT w is minimized
and for all (xi, yi), i=1..n : yi (wTxi + b) ≥ 1
Dr.
Prasenjit
Dey

7. Mathematical representation of the linear SVM
• Let the training set is {(xi, yi)}i=1..n, xiRd, yi  {-1, 1} and the hyperplane with
margin ρ is the separator for the training set.
wTxi + b ≤ - ρ/2 if yi = -1
wTxi + b ≥ ρ/2 if yi = 1
or, yi(wTxi + b) ≥ ρ/2
• Then for each training sample (xi, yi):
r
ρ
Dr.
Prasenjit
Dey

8. Linear and non-linear data
0
0
0
x2
x
x
x
• For linearly separable data, SVM is perform well even the data contain noise.
• However, if the data are non-linear, for SVM it is too hard to draw the separator line.
• Solution: Map the data into a the higher dimensional space:
Dr.
Prasenjit
Dey

9. Non-linear data: example 1
Hyperplane in the higher
dimension
• The original feature space can always be mapped to some higher dimensional feature space
where the training set is separable.
Dr.
Prasenjit
Dey

10. Non-linear data: example 2
• For this hyperplane, three red dots are fall into
the blue categories (misclassification)
• Here, the classification is not perfect
• This separator removes the misclassification.
However, it is difficult to train model like this
• For this, the regularization parameter is
required
Dr.
Prasenjit
Dey

11. • The linear classifier relies on inner product between vectors K(xi,xj) = xi
Txj
• If every datapoint is mapped into high-dimensional space via some transformation Φ: x → φ(x), the inner
product becomes: K(xi,xj)= φ(xi) Tφ(xj)
• A kernel function is a function that is equivalent to an inner product in some feature space.
• Example: 2-dimensional vectors x=[x1 x2]; let K(xi,xj) = (1 + xi
Txj)2
,
Need to show that K(xi,xj) = φ(xi) Tφ(xj):
K(xi,xj)=(1 + xi
Txj)2
,= 1+ xi1
2xj1
2 + 2 xi1xj1 xi2xj2+ xi2
2xj2
2 + 2xi1xj1 + 2xi2xj2=
= [1 xi1
2 √2 xi1xi2 xi2
2 √2xi1 √2xi2]T [1 xj1
2 √2 xj1xj2 xj2
2 √2xj1 √2xj2] =
= φ(xi) Tφ(xj), where φ(x) = [1 x1
2 √2 x1x2 x2
2 √2x1 √2x2]
• Thus, a kernel function implicitly maps data to a high-dimensional space (without the need to compute
each φ(x) explicitly).
The Kernel Functions
Dr.
Prasenjit
Dey

12. The various kernel functions
• Linear: K(xi,xj)= xi
Txj
Mapping Φ: x → φ(x), where φ(x) is x itself
• Polynomial of power p: K(xi,xj)= (1+ xi
Txj)p
Mapping Φ: x → φ(x), where φ(x) has dimensions
• Gaussian (radial-basis function): K(xi,xj) =
Mapping Φ: x → φ(x), where φ(x) is infinite-dimensional
 every point is mapped to a function (a Gaussian)
 combination of functions for support vectors is the separator.
2
2
2
j
i
e
x
x 








 
p
p
d
Dr.
Prasenjit
Dey

13. The main idea of SVM is summarized below
• Margin, Regularization, Gamma, Kernel
• Define an optimal hyperplane: maximize the margin
• Generalize to non-linearly separable problems: use penalty based regularization to deal with the
misclassification
• Map the data into a higher dimensional space where it is easier to classify with linear decision
surface: use the kernel function for transformation of the data from one feature space to another.
Tunable parameters of SVM
Dr.
Prasenjit
Dey

14. Regularization
• For non-linearly separable problems, slack variables ξi can be added to allow misclassification of
difficult or noisy examples. Here, the margin is called soft margin
ξi
ξi
• For soft margin classification, the old formulation of objective
is modified:
Find w and b such that
Φ(w) = wTw + CΣξi is minimized
and for all (xi ,yi), i=1..n : yi (wTxi + b) ≥ 1 – ξi, , ξi ≥ 0
• Parameter C can be viewed as a way to control overfitting: it
“trades off” the relative importance of maximizing the margin
and fitting the training data.
Dr.
Prasenjit
Dey

15. The effect of regularization parameter ‘C’:
• For small value of C  large margin (possible of misclassification)  underfitting
• For large value of C  small margin  overfitting
For small C
For large C
Dr.
Prasenjit
Dey

16. Gamma
• Gamma parameter involves with the RBF kernel function. It controls the distance of influence of a single
training point.
• Low values of gamma indicates a large similarity radius which results in more points being grouped
together.
• For high values of gamma, the points need to be very close to each other in order to be considered in the
same group (or class).
Low gamma
High gamma
Dr.
Prasenjit
Dey

17. The effect of Gamma:
Gamma=0.001
Gamma=0.01
Gamma=0.1 Gamma=1 (Chances of overfitting)
(Considering as one class)
Dr.
Prasenjit
Dey

18. Thank you
Dr.
Prasenjit
Dey