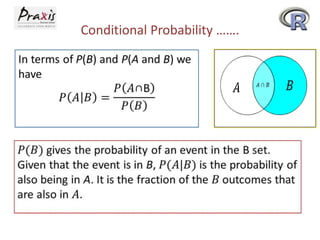
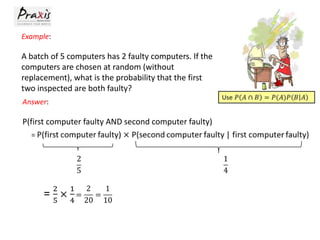
This document discusses probability and related concepts. It covers: - Defining probability and methods of assigning probabilities. - Classical probability and how it assigns probabilities based on outcomes. - Key probability terms like sample space, events, experiments, and trials. - Laws of probability like addition, multiplication, and conditional probability. - Examples are provided to illustrate concepts like independent events and finding probabilities.

1. Probability and Inferential Statistics
• Probability – probability of occurrences are
assigned in the inferential process under
conditions of uncertainty

2. Methods of assigning
probability
• Classical method of assigning probability
(rules and laws)
• Relative frequency of occurrence
(cumulated historical data)
• Subjective Probability (personal intuition
or reasoning)

3. Classical probability:
Assigning probability
• Each outcome is equally likely
• Number of outcomes leading to the event
divided by the total number of outcomes
possible which is denoted as
P(E) = ne/N
where N = total number of outcomes, and
ne = number of outcomes in event E
P(E) = probability of event E

4. Classical probability:
Assigning probability …. continued
Probability of event E can also be defined as
Number of outcomes favourable for E to occur
divided by
Total number of outcomes in Sample space S
Measured on a scale between 0 and 1 inclusive. If E is impossible
P(E) = 0, if E is certain then P(E) = 1.

5. Probability and related terms:
Experiment and Trial
• The process of observing a phenomenon that has
variation in its outcomes.
• The term is used in a broad sense to include any
operation of data collection or observation where
the outcomes are subject to variation.
• Examples: rolling a die, drawing a card from a shuffled deck,
sampling a number of customers for an opinion survey
• Trial is the occurrence and any repetition of an
experiment.

6. Probability and related terms:
Sample space and Event
• Sample space: The collection of all possible
distinct outcomes of an experiment. Denoted
by S.
• Elementary outcome/ Simple event/ Element
of the sample space: Each outcome of an
experiment.
• Event: The collection of elementary outcomes
possessing a designated feature. An event A
occurs when any one of the elementary
outcomes in A occurs.

7. Four Types of Probability
Marginal
Union
Joint
Conditional
P( X )
P( X Y )
P( X Y )
P( X| Y )
The probability
of both X and Y
occurring
The probability
of X occurring
given that Y
has occurred
The probability
of an event X
occurring
X
The probability
of X or Y or
both occurring
X Y
X Y
Y

8. General Law of Addition
For any two events and ,
( or ) = ( ∪ ) = ( ) + ( ) − ( ∩ )
+
-
=

9. General Law of Addition … Example
P( N
.56
S)
P( N ) .70
S
N
.70
S ) P( N ) P ( S ) P ( N
.67
P( S ) .67
P( N S ) .56
P( N
S ) .70 .67 .56
0.81

10. Complement rule

11. Law of Multiplication
• As we know, the intersection of two events is
called the joint probability
• General law of multiplication is used to find the
joint probability
• General law of multiplication gives the probability
that both events x and y will occur at the same
time
• P(x|y) is a conditional probability that can be
stated as the probability of x given y

12. Law of Conditional Probability
• If A and B are two events, the conditional
probability of A occurring given that B is
known or has occurred is expressed as P(A|B)
• The conditional probability of A given B is the
joint probability of A and B divided by the
marginal probability of B.
P( A B)
P( A | B)
P( B)
P( B | A) P( A)
P( B)

13. Conditional Probability …….

14. Conditional Probability : Examples
• P(card is a heart | it is a red suit) = ½
• P(Tomorrow is Tuesday | it is Monday) = 1
• P(result of coin toss is heads | the coin is fair)
=1/2

15. Example:
A batch of 5 computers has 2 faulty computers. If the
computers are chosen at random (without
replacement), what is the probability that the first
two inspected are both faulty?
Answer:
P(first computer faulty AND second computer faulty)

16. Drawing cards
Drawing two random cards from a pack
without replacement, what is the
probability of getting two hearts?
[13 of the 52 cards in a pack are hearts]
1.
2.
3.
4.
1/16
3/51
3/52
1/4
46%
31%
14%
1
2
3
10%
4

17. Drawing cards
Drawing two random cards from a
pack without replacement, what is the
probability of getting two hearts?
To start with 13/52 of the cards are hearts.
After one is drawn, only 12/51 of the remaining
cards are hearts.
So the probability of two hearts is

18. Throw of a die
Throwing a fair dice, let events be
A = get an odd number
B = get a 5 or 6
What is P(A or B)?

19. Alternative
“Probability of not getting either A or B = probability of not getting A and not getting B”
=
Complements Rule
=
i.e. P(A or B) = 1 – P(“not A” and “not B”)

20. Throw of a dice
Throwing a fair dice, let events be
A = get an odd number
B = get a 5 or 6
What is P(A or B)?
Alternative answer

21. Lots of possibilities
then
P(can get to work) = P(A clear or B clear or C clear)
= 1 – P(A blocked and B blocked and C blocked

22. Problems with a device
There are three common ways for a system to experience problems,
with independent probabilities over a year
A = overheats, P(A)=1/3
B = subcomponent malfunctions, P(B) = 1/3
C = damaged by operator, P(C) = 1/10
What is the probability that the system has one or more of these
problems during the year?
1.
2.
3.
4.
5.
1/3
2/5
3/5
3/4
5/6
57%
24%
6%
4%
1
2
3
4
9%
5

23. Problems with a device
There are three common ways for a system to experience
problems, with independent probabilities over a year
A = overheats, P(A)=1/3
B = subcomponent malfunctions, P(B) = 1/3
C = damaged by operator, P(C) = 1/10
What is the probability that the system has one or more of these
problems during the year?

24. B
A
E.g. Throwing a fair dice,
P(getting 4,5 or 6)
= P(4)+P(5)+P(6) = 1/6+1/6+1/6=1/2
C

25. Rules of probability recap

26. Independent Events :
Special Multiplication Rule
If two events A and B are independent then P(A| B) =
P(A) and P(B| A) = P(B): knowing that A has occurred
does not affect the probability that B has occurred and
vice versa.
Probabilities for any number of independent events can
be multiplied to get the joint probability.

27. Independent Events : Example
E.g. A fair coin is tossed twice, what is the chance of getting a
head and then a tail?
P(H1 and T2) = P(H1)P(T2) = ½ x ½ = ¼.
E.g. Items on a production line have 1/6 probability of being
faulty. If you select three items one after another, what is the
probability you have to pick three items to find the first faulty
one?