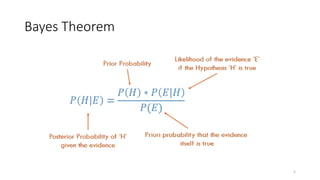
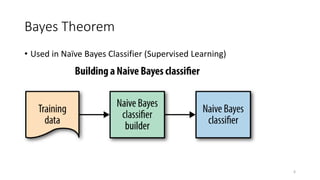
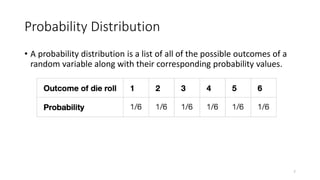
This document discusses probability distributions and related concepts. It defines joint probability, conditional probability, and Bayes' theorem. It then discusses discrete and continuous probability distributions, giving examples of constructing probability mass functions for discrete random variables. It also defines key metrics for probability distributions like mean, variance, and standard deviation, providing examples of calculating these for given data sets. Finally, it discusses examples of discrete probability distributions for scenarios involving dice rolls, coin tosses, and raffle tickets.

1. Probability and Statistics
Week 2 – Mean and Standard Deviation, Probability Distribution
Dr. Ferdin Joe John Joseph

2. Joint Probability
• Probability of events A and B denoted by P(A and B) or P(A ∩ B) is the
probability that events A and B both occur.
• P(A ∩ B) = P(A). P(B)
• This only applies if A and B are independent, which means that if A
occurred, that doesn’t change the probability of B, and vice versa.
2

3. Conditional Probability
• A and B are not independent
• When A and B are not independent, it is often useful to compute the
conditional probability, P (A|B)
• The probability of A given that B occurred: P(A|B) =
P(A ∩ B)
P(B)
• Similarly, P(B|A) =
P(A ∩ B)
P(A)
3

4. • Joint probability of A and B can be denoted as
• P(A ∩ B)= p(A).P(B|A)
4

5. Bayes Theorem
5

6. Bayes Theorem
• Used in Naïve Bayes Classifier (Supervised Learning)
6

7. Probability Distribution
• A probability distribution is a list of all of the possible outcomes of a
random variable along with their corresponding probability values.
7

8. Discrete Probability Distribution
• If we consider 1 and 2 as outcomes of rolling a six-sided die, then we
can’t have an outcome in between that (e.g. We can’t have an
outcome of 1.5).
• This is called probability mass function
8

9. Mean
• Let the data points be 600, 470, 170, 430, 300
• Total elements n = 5
• Mean =
600 +470+170+430+300
5
=
1970
5
= 394
9

10. Variance
• Let the data points be 600, 470, 170, 430, 300
• Total elements n = 5
• Variance =
600 −𝑚𝑒𝑎𝑛 2
+ 470 −𝑚𝑒𝑎𝑛 2
+ 170 −𝑚𝑒𝑎𝑛 2
+ 430 −𝑚𝑒𝑎𝑛 2
+ 300 −𝑚𝑒𝑎𝑛 2
5
=
600 −394 2
+ 470 −394 2
+ 170 −394 2
+ 430 −394 2
+ 300 −394 2
5
10

11. Variance σ2
σ2= 108520/5
σ2= 21704
11

12. Standard Deviation
• Standard Deviation (SD) or σ = 𝑉𝑎𝑟𝑖𝑎𝑛𝑐𝑒
• σ = 21704 = 147.32
12

13. Probability Distribution
13

14. Example
14

15. Example
15

16. Discrete Probability Distributions
• A discrete random variable assumes each of its values with a certain
probability.
• In the case of tossing a coin three times, the variable X, representing
the number of heads, assumes the value 2 with probability 3/8, since
3 of the 8 equally likely sample points result in two heads and one
tail.
16

17. Discrete Probability Distribution
• the probability that no employee gets back the right helmet, that is,
the probability that M assumes the value 0, is 1/3. The possible
values m of M and their probabilities are
17

18. Discrete Probability Distribution
• Frequently, it is convenient to represent all the probabilities of a
random variable X by a formula. Such a formula would necessarily be
a function of the numerical values x that we shall denote by f(x), g(x),
r(x), and so forth. Therefore, we write f(x) = P(X = x); that is, f(3) = P(X
= 3).
• The set of ordered pairs (x, f(x)) is called the probability function,
probability mass function, or probability distribution of the discrete
random variable X.
18

19. Discrete Probability Distribution
19

20. Example
• A shipment of 20 similar laptop computers to a retail outlet contains 3
that are defective. If a school makes a random purchase of 2 of these
computers, find the probability distribution for the number of
defectives.
20

21. Solution
• Let X be a random variable whose values x are the possible numbers
of defective computers purchased by the school. Then x can only take
the numbers 0, 1, and 2.
21

22. Exercise
• If a car agency sells 50% of its inventory of a certain foreign car
equipped with side airbags, find a formula for the probability
distribution of the number of cars with side airbags among the next 4
cars sold by the agency.
22

23. Solution
23

24. Example
• Let the random variable X represents the number of boys in a family.
a) Construct the probability distribution for a family of two children.
b) Find the mean and standard deviation of X.
24

25. Solution
a) We first construct a tree diagram to represent all possible
distributions of boys and girls in the family.
25

26. Solution
• Assuming that all the above possibilities are equally likely, the
probabilities are:
• P(X=2) = P(BB) = 1 / 4
• P(X=1) = P(BG) + P(GB) = 1 / 4 + 1 / 4 = 1 / 2
• P(X=0) = P(GG) = 1 / 4
26

27. Solution
• The discrete probability distribution of X is given by
X P(X)
0 1 / 4
1 1 / 2
2 1 / 4
27

28. Solution
• Note that ∑ P(X) = 1
b) The mean µ of the random variable X is defined by
µ = ∑ X P(X)
= 0 * (1/4) + 1 * (1/2) + 2 * (1/4) = 1
28

29. Solution
• The standard deviation σ of the random variable X is defined by
SD = Square Root [ ∑ (X- µ) 2 P(X) ]
= (0 − 1) 2 ∗ (1/4) + (1 − 1) 2 ∗ (1/2) + (2 − 1) 2 ∗ (1/4)
= 1 / 2
= 1/1.414
29

30. Exercise
Two balanced dice are rolled. Let X be the sum of the two dice.
a) Obtain the probability distribution of X.
b) Find the mean and standard deviation of X.
30

31. Solution
a) When the two balanced dice are rolled, there are 36 equally likely
possible outcomes as shown below.
31

32. Solution
• The possible values of X are: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12.
• The possible outcomes are equally likely hence the probabilities P(X) are given by
• P(2) = P(1,1) = 1 / 36
• P(3) = P(1,2) + P(2,1) = 2 / 36 = 1 / 18
• P(4) = P(1,3) + P(2,2) + P(3,1) = 3 / 36 = 1 / 12
• P(5) = P(1,4) + P(2,3) + P(3,2) + P(4,1) = 4 / 36 = 1 / 9
• P(6) = P(1,5) + P(2,4) + P(3,3) + P(4,2) + P(5,1)= 5 / 36
• P(7) = P(1,6) + P(2,5) + P(3,4) + P(4,3) + P(5,2) + P(6,1) = 6 / 36 = 1 / 6
• P(8) = P(2,6) + P(3,5) + P(4,4) + P(5,3) + P(6,2) = 5 / 36
• P(9) = P(3,6) + P(4,5) + P(5,4) + P(6,3) = 4 / 36 = 1 / 9
• P(10) = P(4,6) + P(5,5) + P(6,4) = 3 / 36 = 1 / 12
• P(11) = P(5,6) + P(6,5) 2 / 36 = 1 / 18
• P(12) = P(6,6) = 1 / 36
32

33. Solution
• The discrete probability distribution of X is given by
• X P(X)
• 2 1 / 36
• 3 1 / 18
• 4 1 / 12
• 5 1 / 9
• 6 5 / 36
• 7 1 / 6
• 8 5 / 36
• 9 1 / 9
• 10 1 / 12
• 11 1 / 18
• 12 1 / 36
As an exercise, check that ∑ P(X) = 1 33

34. Solution
• b) The mean of X is given by
• µ = ∑ X P(X)
= 2*(1/36)+3*(1/18)+4*(1/12)+5*(1/9)+6*(5/36)+7*(1/6)+8*(5/36)
+9*(1/9)+10*(1/12)+11*(1/18)+12*(1/36)
= 7
34

35. Solution
• The standard deviation of is given by
SD = √ [ ∑ (X- µ) 2 P(X) ]
= √[ (2-7)2*(1/36)+(3-7)2*(1/18)
+(4-7)2*(1/12)+(5-7)2*(1/9)+(6-7)2*(5/36)
+(7-7)2*(1/6)+(8-7)2*(5/36)+(9-7)2*(1/9)
+(10-7)2*(1/12)+(11-7)2*(1/18)+(12-7)2*(1/36) ]
= 2.41
35

36. Exercise
1. Three coins are tossed. Let X be the number of heads obtained. Construct a probability
distribution for X and find its mean and standard deviation.
2. A fair coin is tossed twice. Let X be the number of heads that are observed.
• Construct the probability distribution of X.
• Find the probability that at least one head is observed.
3. A service organization in a large town organizes a raffle each month. One thousand raffle tickets
are sold for $1 each. Each has an equal chance of winning. First prize is $300, second prize is $200,
and third prize is $100. Let X denote the net gain from the purchase of one ticket.
• Construct the probability distribution of X.
• Find the probability of winning any money in the purchase of one ticket.
• Find the expected value of X, and interpret its meaning.
36

37. Solutions
• Click Here
37

38. 38