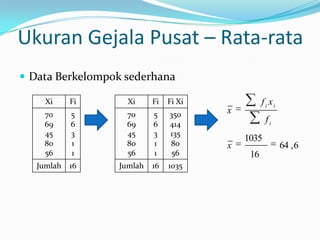
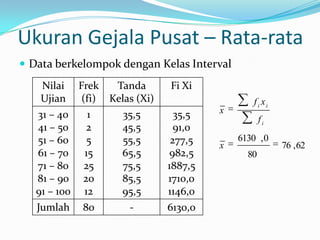
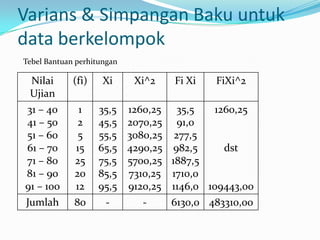
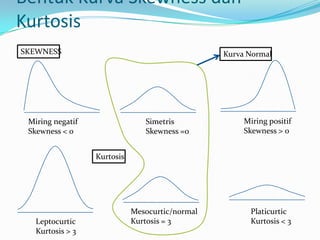
Dokumen ini membahas statistika deskriptif, yang mencakup teknik pengumpulan, penyajian, dan analisis data untuk menarik kesimpulan. Ia menjelaskan berbagai ukuran seperti rata-rata, median, modus, kuartil, desil, dan persentil, serta varians dan simpangan baku untuk menganalisis data tunggal dan berkelompok. Selain itu, diulas juga konsep skewness dan kurtosis untuk menggambarkan distribusi data.

2. STATISTIKA
ilmu yang mempelajari/berkaitan dengan
 Pengumpulan data
 Penyajian data
 Pengolahan data
 Menarik kesimpulan/menginterpretasi hasil
pengolahan dat

3. STATISTIKA DESKRIPTIF
Digunakan apabila peneliti hanya bertujuan untuk
mendapatkan ringkasan data yang dimilikinya.
Ringkasan ini meliputi lokasi pemusatan
data, variabilitas data dan karakteristik umum
distribusi data.

4. STATISTIKA DESKRIPTIF
 Collect
 Organize
 Summarize
 Display
 Analyze
Kesimpulan yang di ambil dari analisis statistika
deskriptif hanya berlaku untuk data yang sedang
diamati/diteliti

5. Statistika Deskriptif Meliputi :
Ukuran Gejala Pusat Ukuran Dispersi
(Pemusatan Data) (Penyebaran Data)
1. Rata-rata (Mean) 1. Jangkauan (rentang)
2. Nilai Tengah 2. Variasi (Varians)
(Median) 3. Simpangan Baku
3. Modus (Standard Deviation)
Ukuran Letak Data Ukuran Lain
1. Kuartil 1. Skewness
2. Desil 2. Kurtosis
3. Persentil 3. Bilangan Baku

6. Ukuran Gejala Pusat – Rata-rata
 Untuk Data Tunggal
n
xi Dimana : xi = nilai data pengamatan ke i
i 1
n = jumlah data atau banyaknya
x i 1, 2 ,3 ,  , n data di dalam sample
n
 Untuk data yang berkelompok (data yang disusun dalam
daftar distribusi frekuensi)
Dimana :
f i xi
x fi = frekuensi untuk kelas interval ke-i
fi xi = nilai tengah untuk kelas interval ke-i

7. Ukuran Gejala Pusat – Rata-rata
 Data Tunggal
Nilai ujian statistika 5 sbb : 70, 69, 45, 80, 56.
Rata-rata (mean) adalah
n
xi 2 2 2 2 2
i 1
x1 x2 x3 x4 x5
x
n n
70 69 45 80 56
x 64
5

8. Ukuran Gejala Pusat – Rata-rata
 Data Berkelompok sederhana
Xi Fi Xi Fi Fi Xi f i xi
70 5 70 5 350 x
69 6 69 6 414
fi
45 3 45 3 135
1035
80 1 80 1 80 x 64 , 6
56 1 56 1 56 16
Jumlah 16 Jumlah 16 1035

9. Ukuran Gejala Pusat – Rata-rata
 Data berkelompok dengan Kelas Interval
Nilai Frek Tanda Fi Xi
Ujian (fi) Kelas (Xi) f i xi
31 – 40 1 35,5 35,5 x
fi
41 – 50 2 45,5 91,0
51 – 60 5 55,5 277,5 6130 , 0
x 76 , 62
61 – 70 15 65,5 982,5 80
71 – 80 25 75,5 1887,5
81 – 90 20 85,5 1710,0
91 – 100 12 95,5 1146,0
Jumlah 80 - 6130,0

10. Ukuran Gejala Pusat – Median
 Untuk data Tunggal (setelah data disusun dari data terkecil
hingga data terbesar)
Dimana : xi = nilai data pengamatan ke i
x n 1 / 2 , jika n ganjil n = jumlah data atau banyaknya
Me data di dalam sample
xn 2
x n 2 1
, jika n genap
2
 Untuk data berkelompok
Dimana :
n F Li = Batas bawah kelas median, yaitu kelas dimana
Me Li 2 p median berada
f p = panjang kelas interval
n = jumlah data
F = Frekuensi kumulatif sebelum kelas median
f = frekuensi kelas dimana median berada

11. x n 1 / 2 , jika n ganjil
Median Me xn 2
x n 2 1
, jika n genap
2
 Data Tunggal
a. n ganjil : 4 12 5 7 8 Urutkan 4 5 7 8 12 maka
data
mediannya adalah x( n 1) / 2
x(5 1) / 2
x3 7
Urutkan
b. n genap : 4 12 5 7 9 11 data
4 5 7 9 11 12
maka mediannya adalah
xn xn
2 2
1 x3 x4 7 9
8
2 2 2

12. Median (data berkelompok)
Nilai Frek Letak nilai median ada di data ke 40, maka letak
Ujian (fi) median ada pada kelas interval ke 5.
31 – 40 1 n
2
F
41 – 50 2 Me Li p
f
51 – 60 5
61 – 70 15 L5 batas baw ah kelas int erval ke 5 70, 5
71 – 80 25 p 10, f 25, F 1 2 5 15 23
81 – 90 20
80
91 – 100 12 2
23
Me 70, 5 10 77, 3
Jumlah 80 25

13. Ukuran Gejala Pusat – Modus
 Data tunggal
Cukup mencari nilai dengan frekuensi kemunculan
paling banyak
 Data berkelompok
b1
Mo Li p
b1 b2
Dimana :
Li = Batas bawah kelas modus, yaitu kelas interval
dengan frekuensi terbanyak
p = panjang kelas interval
b1 = selisih frekuensi kelas modus dengan frekuensi kelas sebelumnya
b2 = selisih frekuensi kelas modus dengan frekuensi kelas sesudahnya

14. MODUS data tunggal
12, 34, 14, 34, 28, 34, 34, 28, 14
Data diatas dapat disusun dalam tabel distribusi
frekuensi sederhana sbb:
Xi Fi Maka modusnya adalah data dengan
frekuensi terbanyak, modus = 34
12 1
14 2
28 3
34 4
Jumlah 10

15. Modus data berkelompok
Nilai Frek Kelas modus =Kelas interval dengan frekuensi
Ujian (fi) terbanyak = kelas interval ke 5
31 – 40 1 b1
M0 Li p
41 – 50 2 b1 b2
51 – 60 5
L5 batas baw ah kelas int erval ke 5 70, 5
61 – 70 15
71 – 80 25 p 10
81 – 90 20 b1 25 15 10
91 – 100 12 b2 25 20 5
Jumlah 80 10
Me 70, 5 10 77,17
10 5

16. Ukuran Letak – Kuartil
ukuran letak yang membagi distribusi suatu data menjadi 4 bagian yang sama, sesudah
data disusun urutan nilainya dari nilai terkecil hingga nilai yang terbesar
 Untuk data tunggal maka kuartil ke-i berada di :
i n 1
L eta k K i d a ta ke , d en g a n i 1, 2, d a n 3
4
 Untuk data berkelompok
i .n F
Ki L 4 p , dengan i 1, 2, dan 3
f
Dimana :
L = Batas bawah kelas Ki, yaitu kelas interval dimana Ki berada
p = panjang kelas interval
n = jumlah data
F = Frekuensi kumulatif sebelum kelas Ki
f = frekuensi kelas dimana Ki berada

17. Ukuran Letak – Desil
ukuran letak yang membagi distribusi suatu data menjadi 10 bagian yang sama, sesudah
disusun urutan nilainya dari nilai terkecil hingga nilai yang terbesar
 Untuk data tunggal maka Desil ke-i berada di :
i n 1
L eta k D i d a ta ke , d en g a n i 1, 2, 3,  , d a n 9
10
 Untuk data berkelompok
i .n F
Di L 10 p , dengan i 1, 2,  , dan 9
f
Dimana :
L = Batas bawah kelas Di, yaitu kelas interval dimana Di berada
p = panjang kelas interval
n = jumlah data
F = Frekuensi kumulatif sebelum kelas Di
f = frekuensi kelas dimana Di berada

18. Ukuran Letak – Persentil
ukuran letak yang membagi distribusi suatu data menjadi 100 bagian yang sama,
sesudah data disusun urutan nilainya dari nilai terkecil hingga nilai yang terbesar
 Untuk data tunggal maka Persentil ke-i berada di :
i n 1
L eta k Pi d a ta ke , d en g a n i 1, 2, 3,  , d a n 9 9
100
 Untuk data berkelompok
i .n F
Pi L 100 p , dengan i 1, 2,  , dan 99
f
Dimana :
L = Batas bawah kelas Pi, yaitu kelas interval dimana Pi berada
p = panjang kelas interval
n = jumlah data
F = Frekuensi kumulatif sebelum kelas Pi
f = frekuensi kelas dimana Pi berada

19. Langkah-langkah menentukan
Median, Kuartil, Desil dan Persentil
1. Urutkan data
2. Tentukan letak median, kuartil, desil dan persentil
3. Tentukan nilai median, kuartil, desil dan persentil
Catatan : Berikut ini diberikan contoh cara
menentukan persentil untuk data tunggal
dan data berkelompok, untuk desil dan
kuartil diperoleh dengan cara yang sama.

20. Persentil Data Tunggal
75, 82, 66, 57, 64, 56, 92, 94, 86, 52, 60, 70 disusun menjadi
52, 56, 57, 60, 64, 66, 70, 75, 82, 86, 92, 94
Tentukan P75 !
75(12 1)
L etak P75 data ke data ke 9, 75
100
nilai P75 data ke 9 0, 75( data ke 10 data ke 9)
82 0, 75(86 82)
82 3 85
Arti P75 = 85, pada data di atas adalah :
“Sebanyak 75 % bagian dari data yang ada nilainya dibawah 85
dan 25% bagian lagi nilainya ada di atas 85”

21. Persentil 75 untuk (data berkelompok)
Letak persentil ke 75 ada pada data ke 0,75 x 80 = 60,
Nilai Frek maka letak median ada pada kelas interval ke 6.
Ujian (fi)
i .n F
31 – 40 1 P7 5 L6 100 p
41 – 50 2 f
51 – 60 5
L6 batas baw ah kelas int erval ke 6 80, 5
61 – 70 15
71 – 80 25 p 10, f 20, F 1 2 5 15 25 48
81 – 90 20 (75)80
48
91 – 100 12 P75 80, 5 100 10
20
Jumlah 80
80, 5 6 86, 5

22. INTERPRETASI HASIL :
Nilai Frek
Ujian (fi)
31 – 40 1 P75 86, 5
41 – 50 2
51 – 60 5
61 – 70 15 Artinya :
71 – 80 25 “Sebanyak 75 % bagian dari
81 – 90 20 data yang ada nilainya dibawah
91 – 100 12 86,5 dan 25% bagian lagi
nilainya ada di atas 86,5”
Jumlah 80

23. Ukuran Dispersi – Varians &
Simpangan Baku
 Varians Untuk Data Tunggal : 2
n
n n
xi
2 2 i 1
xi x xi
2 i 1 i 1 n
s
n 1 n 1
 Varians untuk data berkelompok :
n
2 Dimana :
n n
f i xi xi = Nilai tengah kelas interval ke – i
fi = frekuensi kelas interval ke – i
2 2 i 1
f i xi x f i xi
n
s
2 i 1 i 1
n = Jumlah data (Jumlah frekuensi)
n 1 n 1
Sehingga Simpangan Baku (standar deviasi) : s s
2

24. Varians dan simpangan baku untuk
data tunggal n
2
n
xi
Misalkan data sbb : 8, 7, 10, 11, 4 2
xi
i 1
n
Tabel bantuan perhitungan untuk varians s
2 i 1
n 1
2
Xi Xi ^2 40
8 64 350
80 7, 5
7 49
10 100 80 1
11 121
4 16 Simpangan Baku :
40 350
2
s s 7, 5 2, 74

25. Varians & Simpangan Baku untuk
data berkelompok
Tebel Bantuan perhitungan
Nilai (fi) Xi Xi^2 Fi Xi FiXi^2
Ujian
31 – 40 1 35,5 1260,25 35,5 1260,25
41 – 50 2 45,5 2070,25 91,0
51 – 60 5 55,5 3080,25 277,5
61 – 70 15 65,5 4290,25 982,5 dst
71 – 80 25 75,5 5700,25 1887,5
81 – 90 20 85,5 7310,25 1710,0
91 – 100 12 95,5 9120,25 1146,0 109443,00
Jumlah 80 - - 6130,0 483310,00

26. Var & Simp. Baku
Varians :
6310
483310
s
2 80 172,1
80 1
Simpangan Baku :
2
s 1 7 2,1 1 3 .1 2

27. Ukuran Lain
xi x
 Bilangan Baku z i
s
 Skewness : ukuran kesimetrisan distribusi data
rata rata m od us x Mo
Skew ness
sim pangan baku s
 Kurtosis : Ukuran datar atau runcingnya distribusi data
Koefisien Kurtosis persentil :
1 K 3 K1
K u rto sis 2
P9 0 P1 0

28. Bentuk Kurva Skewness dan
Kurtosis
SKEWNESS Kurva Normal
Miring negatif Simetris Miring positif
Skewness < 0 Skewness =0 Skewness > 0
Kurtosis
Mesocurtic/normal Platicurtic
Leptocurtic Kurtosis = 3 Kurtosis < 3
Kurtosis > 3

29. Tugas dengan menggunakan Data!
Buktikan bahwa
1. Me = K2 = D5 = P50
2. K1 = P25
3. K3 = P75