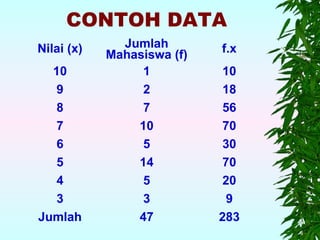
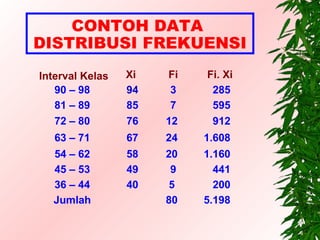
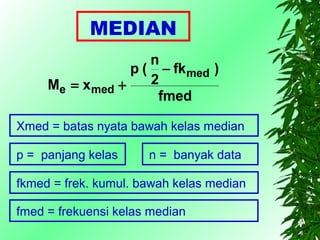
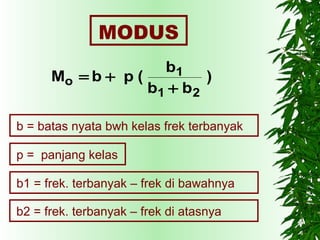
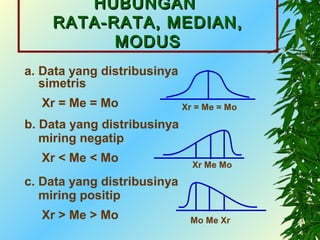
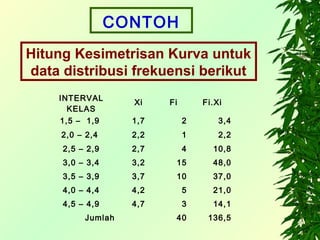
Dokumen ini membahas ukuran statistik untuk data populasi dan sampel, mencakup pengertian rata-rata, median, dan modus dengan contoh perhitungan. Dikenalkan pula konsep distribusi frekuensi serta hubungan antara rata-rata, median, dan modus dalam konteks kesimetrisan data. Selain itu, dokumen ini juga menjelaskan kemiringan kurva dan kaidah empirik terkait sebaran data.

1. KULIAH BAB III
UKURAN
STATISTIK
BAGI DATA

2. POPULASI
DAN SAMPEL
POPULASI SAMPEL
SELURUH HIMPUNAN
PENGAMATAN BAGIAN DARI
YANG DIKAJI POPULASI

3. Rata-rata
(Nilai Tengah )
UKURAN
Median GEJALA Modus
PUSAT
Kuartil,
Desil,
Persentil

4. DATA TAK
BERKELOMPOK

5. RATA-RATA
n
∑ i
x
x r =i=1
n
Xi = Nilai Data ke i
n = Jumlah Data
Xr = Nilai rata-rata

6. CONTOH
Diperoleh data :
3, 5, 6, 4, dan 6
X rata-rata
= (3 + 5 + 6 + 4 + 6)/5
= 4,8

7. MEDIAN
segugus data x1, x2, ….., xn,
yang telah diurutkan, maka
median adalah data yang
tepat di tengah urutan
Data : 79 82 86 92
93
Median = 86
Data : 1,9 2,3 2,5 2,7 2,9
3,1
Median = (2,5 + 2,7)/2 = 2,6

8. MODUS
adalah nilai paling sering
muncul atau berfrekuensi
tertinggi
Tidak selalu ada namun
bisa juga lebih dari satu

9. CONTOH
Data: 9 10 5 9 9 7 8 6 10
11
Modus = 9
Data: 2 0 3 1 2 4 2 5 4 0
1 4
Modus = 2 dan 4 Bimodus
Data: 79 82 86 92 93
Modus = tidak ada

10. DATA
BERKELOMPOK
SEDERHANA

11. CONTOH DATA
Nilai (x) Jumlah f.x
Mahasiswa (f)
10 1 10
9 2 18
8 7 56
7 10 70
6 5 30
5 14 70
4 5 20
3 3 9
Jumlah 47 283

12. RATA-RATA
n
∑fx i
x r = i=1
n
Nilai rata-rata pada
contoh adalah
X = 283/47 = 6,02

13. MEDIAN
Jumlah mahasiswa pada
contoh n = 47 siswa
Nilai tengah terletak pada
data ke (47 + 1)/2 = 24
Data ke 24 terletak pada
baris 5 dengan nilai 6
Median = 6

14. MODUS
Frekuensi terbesar pada
tabel = 14
Nilai dengan frekuensi
terbesar = 5
Modus = 5

15. DATA
DISTRIBUSI
FREKUENSI

16. CONTOH DATA
DISTRIBUSI FREKUENSI
Interval Kelas Xi Fi Fi. Xi
90 – 98 94 3 285
81 – 89 85 7 595
72 – 80 76 12 912
63 – 71 67 24 1.608
54 – 62 58 20 1.160
45 – 53 49 9 441
36 – 44 40 5 200
Jumlah 80 5.198

17. RATA-RATA
n
∑ xi
f
x r =i=1
n
Nilai rata-rata pada
contoh adalah
X = 5.198/80 = 64,975

18. MEDIAN
n
p ( − fk med )
Me = x med + 2
fmed
Xmed = batas nyata bawah kelas median
p = panjang kelas n = banyak data
fkmed = frek. kumul. bawah kelas median
fmed = frekuensi kelas median

19. Hitungan
Jumlah data = 80, median pada data ke 40
Data ke 40 di baris ke-4 di kelas 63 – 71
Kelas 63 – 71 disebut kelas median
Xmed = (63 + 62)/2 = 62,5 p=9
fkmed = 20 + 9 + 5 = 34 n = 80
fmed = 24
Median = 64,75

20. MODUS
b1
Mo = b + p ( )
b1 + b2
b = batas nyata bwh kelas frek terbanyak
p = panjang kelas
b1 = frek. terbanyak – frek di bawahnya
b2 = frek. terbanyak – frek di atasnya

21. Hitungan
Frek. terbanyak 24 ada di kelas
63 – 71
b = 62,5 p=9
b1 = 24 – 20 = 4 b2 = 24 – 12 = 12
Modus = 64,75

22. HUBUNGAN
RATA-RATA, MEDIAN,
MODUS
a. Data yang distribusinya
simetris
Xr = Me = Mo Xr = Me = Mo
b. Data yang distribusinya
miring negatip
Xr < Me < Mo Xr Me Mo
c. Data yang distribusinya
miring positip
Xr > Me > Mo Mo Me Xr

23. KESIMETRISAN KURVA
KOEFISIEN
KEMIRINGAN
PEARSON
3 (xr − me)
SK =
s
dimana:
xr = X rata-rata s = Simpangan baku
me = median SK = Koef. Kemiringan
Pearson
SK positip, kurva miring ke kiri. SK negatip,
kurva miring ke kanan. SK mendekati 0, kurva
mendekati simetris. SK = 0, kurva simetris

24. CONTOH
Hitung Kesimetrisan Kurva untuk
data distribusi frekuensi berikut
INTERVAL
Xi Fi Fi.Xi
KELAS
1,5 – 1,9 1,7 2 3,4
2,0 – 2,4 2,2 1 2,2
2,5 – 2,9 2,7 4 10,8
3,0 – 3,4 3,2 15 48,0
3,5 – 3,9 3,7 10 37,0
4,0 – 4,4 4,2 5 21,0
4,5 – 4,9 4,7 3 14,1
Jumlah 40 136,5

25. JAWAB
1. Hitung Xr = xi.fi / n
= 136,5/40 = 3,41
2. Hitung Me = 2,95 + 0,5(20-7)/15
= 2,95 + 0,43 = 3,38
3. Hitung s = 0,70
4. Hitung kemiringan Pearson
SK = 3(xr – me)/s = 0,12
Nilai SK 0,12 positip berarti data
sedikit menjulur ke kiri, agak simetris

26. MENGHITUNG
SIMPANGAN
BAKU
n
∑fi ( x i −x r )2
s = i=1
n−1
s = simpangan baku
n = banyak pengamatan
f = frekuensi
xi = data pengamatan
xr = x rata-rata

27. Lengkapi Tabel
Xr = 3,41
INTERVA Xi –
Xi Fi Fi.Xi (Xi – Xr) 2 f(Xi – Xr) 2
L KELAS Xr
1,5 – 1,9 1,7 2 3,4 – 1,71 2,9241 5,8482
2,0 – 2,4 2,2 1 2,2 – 1,21 1,4641 1,4641
2,5 – 2,9 2,7 4 10,8 – 0,71 0,5041 2,0164
3,0 – 3,4 3,2 15 48,0 – 0,21 0,0441 0,6615
3,5 – 3,9 3,7 10 37,0 0,29 0,0841 0,8410
4,0 – 4,4 4,2 5 21,0 0,79 0,6241 3,1205
4,5 – 4,9 4,7 3 14,1 1,29 1,6641 4,9923
Jumlah 40 136,5 Jumlah 18,9440
s = 0,70

28. KAIDAH EMPIRIK
Pada sebaran data berbentuk
kurva normal, maka kira-kira
a. 68% data terletak dalam 1 kali
simpangan baku dari nilai rata-rata
b. 95% data terletak dalam 2 kali
simpangan baku dari nilai rata-rata
c. 99,7% data terletak dalam 3 kali
simpangan baku dari nilai rata-rata

29. PERSENTIL,
DESIL,
DAN KUARTIL
Persentil adalah pengelompokan data
menjadi 100 bagian sama besar.
Lambangnya P1, P2, …….P99
Desil adalah pengelompokan data
menjadi 10 bagian sama besar.
Lambangnya D1, D2, …….D9
Kuartil adalah pengelompokan data
menjadi 4 bagian sama besar.
Lambangnya Q1, Q2, dan Q3

30. KERJAKAN
TUGAS DAN
LATIHAN
ANDA

31. SEKIAN
DAN
TERIMA KASIH