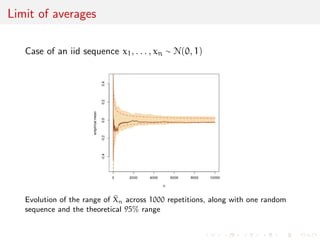
The document discusses statistical models and exponential families. It states that for most of the course, data is assumed to be a random sample from a distribution F. Repetition of observations via the law of large numbers and central limit theorem increases information about F. Exponential families are a class of parametric distributions with convenient analytic properties, where the density can be written as a function of natural parameters in an exponential form. Examples of exponential families include the binomial and normal distributions.

1. Chapter 1 :
statistical vs. real models
Statistical models
Quantities of interest
Exponential families

2. Statistical models
For most of the course, we assume that the data is a random
sample x1, . . . , xn and that
x1, . . . , xn F(x)
as i.i.d. variables or as transforms of i.i.d. variables
Motivation:
Repetition of observations increases information about F, by virtue
of probabilistic limit theorems (LLN, CLT)

3. Statistical models
For most of the course, we assume that the data is a random
sample x1, . . . , xn and that
x1, . . . , xn F(x)
as i.i.d. variables or as transforms of i.i.d. variables
Motivation:
Repetition of observations increases information about F, by virtue
of probabilistic limit theorems (LLN, CLT)
Warning 1: Some aspects of F may ultimately remain unavailable

4. Statistical models
For most of the course, we assume that the data is a random
sample x1, . . . , xn and that
x1, . . . , xn F(x)
as i.i.d. variables or as transforms of i.i.d. variables
Motivation:
Repetition of observations increases information about F, by virtue
of probabilistic limit theorems (LLN, CLT)
Warning 2: The model is always wrong, even though we behave as
if...

5. Limit of averages
Case of an iid sequence x1, . . . , xn N(0, 1)
Evolution of the range of X
n across 1000 repetitions, along with one random
sequence and the theoretical 95% range

6. Limit theorems
Law of Large Numbers (LLN)
If X1, . . . ,Xn are i.i.d. random variables, with a well-de

7. ned
expectation E[X]
X1 + . . . + Xn
n
prob
! E[X]
[proof: see Terry Tao's What's new, 18 June 2008]

8. Limit theorems
Law of Large Numbers (LLN)
If X1, . . . ,Xn are i.i.d. random variables, with a well-de

9. ned
expectation E[X]
X1 + . . . + Xn
n
a.s.
! E[X]
[proof: see Terry Tao's What's new, 18 June 2008]

10. Limit theorems
Law of Large Numbers (LLN)
If X1, . . . ,Xn are i.i.d. random variables, with a well-de

11. ned
expectation E[X]
X1 + . . . + Xn
n
a.s.
! E[X]
Central Limit Theorem (CLT)
If X1, . . . ,Xn are i.i.d. random variables, with a well-de

12. ned
expectation E[X] and a

13. nite variance 2 = var(X),
p
n

14. X1 + . . . + Xn
n
- E[X]
dist.
! N(0, 2)
[proof: see Terry Tao's What's new, 5 January 2010]

15. Limit theorems
Central Limit Theorem (CLT)
If X1, . . . ,Xn are i.i.d. random variables, with a well-de

16. ned
expectation E[X] and a

17. nite variance 2 = var(X),
p
n

18. X1 + . . . + Xn
n
- E[X]
dist.
! N(0, 2)
[proof: see Terry Tao's What's new, 5 January 2010]
Continuity Theorem
If
Xn
dist.
! a
and g is continuous at a, then
g(Xn)
dist.
! g(a)

19. Limit theorems
Central Limit Theorem (CLT)
If X1, . . . ,Xn are i.i.d. random variables, with a well-de

20. ned
expectation E[X] and a

21. nite variance 2 = var(X),
p
n

22. X1 + . . . + Xn
n
- E[X]
dist.
! N(0, 2)
[proof: see Terry Tao's What's new, 5 January 2010]
Slutsky's Theorem
If Xn, Yn, Zn converge in distribution to X, a, and b, respectively,
then
XnYn + Zn
dist.
! aX + b

23. Limit theorems
Central Limit Theorem (CLT)
If X1, . . . ,Xn are i.i.d. random variables, with a well-de

24. ned
expectation E[X] and a

25. nite variance 2 = var(X),
p
n

26. X1 + . . . + Xn
n
- E[X]
dist.
! N(0, 2)
[proof: see Terry Tao's What's new, 5 January 2010]
Delta method's Theorem
If p
nfXn - g
dist.
! Np(0,
)
and g : Rp ! Rq is a continuously dierentiable function on a
neighbourhood of 2 Rp, with a non-zero gradient rg(), then
p
n fg(Xn) - g()g
dist.
! Nq(0,rg()T
rg())

27. Exemple 1: Binomial sample
Case # 1: Observation of i.i.d. Bernoulli variables
xi B(p)
with unknown parameter p (e.g., opinion poll)
Case # 2: Observation of independent Bernoulli variables
xi B(pi)
with unknown and dierent parameters pi (e.g., opinion poll,
u
epidemics)
Transform of i.i.d. u1, . . . , un:
xi = I(ui 6 pi)

28. Exemple 1: Binomial sample
Case # 1: Observation of i.i.d. Bernoulli variables
xi B(p)
with unknown parameter p (e.g., opinion poll)
Case # 2: Observation of conditionally independent Bernoulli
variables
xijzi B(p(zi))
with covariate-driven parameters p(zi) (e.g., opinion poll,
u
epidemics)
Transform of i.i.d. u1, . . . , un:
xi = I(ui 6 pi)

29. Parametric versus non-parametric
Two classes of statistical models:
Parametric when F varies within a family of distributions
indexed by a parameter that belongs to a

30. nite dimension
space :
F 2 fF, 2 g
and to know F is to know which it corresponds to
(identi

31. ability);
Non-parametric all other cases, i.e. when F is not constrained
in a parametric way or when only some aspects of F are of
interest for inference
Trivia: Machine-learning does not draw such a strict distinction
between classes

32. Parametric versus non-parametric
Two classes of statistical models:
Parametric when F varies within a family of distributions
indexed by a parameter that belongs to a

33. nite dimension
space :
F 2 fF, 2 g
and to know F is to know which it corresponds to
(identi

34. ability);
Non-parametric all other cases, i.e. when F is not constrained
in a parametric way or when only some aspects of F are of
interest for inference
Trivia: Machine-learning does not draw such a strict distinction
between classes

35. Non-parametric models
In non-parametric models, there may still be constraints on the
range of F`s as for instance
EF[YjX = x] = (

36. Tx), varF(YjX = x) = 2
in which case the statistical inference only deals with estimating or
testing the constrained aspects or providing prediction.
Note: Estimating a density or a regression function like (

37. Tx) is
only of interest in a restricted number of cases

38. Parametric models
When F = F, inference usually covers the whole of the parameter
and provides
point estimates of , i.e. values substituting for the unknown
true
con

39. dence intervals (or regions) on as regions likely to
contain the true
testing speci

40. c features of (true or not?) or of the whole
family (goodness-of-

41. t)
predicting some other variable whose distribution depends on
z1, . . . , zm G(z)
Inference: all those procedures depend on the sample (x1, . . . , xn)

42. Parametric models
When F = F, inference usually covers the whole of the parameter
and provides
point estimates of , i.e. values substituting for the unknown
true
con

43. dence intervals (or regions) on as regions likely to
contain the true
testing speci

44. c features of (true or not?) or of the whole
family (goodness-of-

45. t)
predicting some other variable whose distribution depends on
z1, . . . , zm G(z)
Inference: all those procedures depend on the sample (x1, . . . , xn)

46. Example 1: Binomial experiment again
Model: Observation of i.i.d. Bernoulli variables
xi B(p)
with unknown parameter p (e.g., opinion poll)
Questions of interest:
1 likely value of p or range thereof
2 whether or not p exceeds a level p0
3 how many more observations are needed to get an estimation
of p precise within two decimals
4 what is the average length of a lucky streak (1's in a row)

47. Exemple 2: Normal sample
Model: Observation of i.i.d. Normal variates
xi N(, 2)
with unknown parameters and 0 (e.g., blood pressure)
Questions of interest:
1 likely value of or range thereof
2 whether or not is above the mean of another sample
y1, . . . , ym
3 percentage of extreme values in the next batch of m xi's
4 how many more observations to exclude zero from likely values
5 which of the xi's are outliers

48. Quantities of interest
Statistical distributions (incompletely) characterised by (1-D)
moments:
central moments
1 = E[X] =
Z
xdF(x) k = E
h
(X - 1)k
i
k 1
non-central moments
k = E
Xk
k 1
quantile
P(X ) =
and (2-D) moments
cov(Xi, Xj) =
Z
(xi - E[Xi])(xj - E[Xj])dF(xi, xj)
Note: For parametric models, those quantities are transforms of
the parameter

49. Example 1: Binomial experiment again
Model: Observation of i.i.d. Bernoulli variables
Xi B(p)
Single parameter p with
E[X] = p var(X) = p(1 - p)
[somewhat boring...]
Median and mode

50. Example 1: Binomial experiment again
Model: Observation of i.i.d. Binomial variables
Xi B(n, p) P(X = k) =
n
k
pk(1 - p)n-k
Single parameter p with
E[X] = np var(X) = np(1 - p)
[somewhat less boring!]
Median and mode

51. Example 2: Normal experiment again
Model: Observation of i.i.d. Normal variates
xi N(, 2) i = 1, . . . , n ,
with unknown parameters and 0 (e.g., blood pressure)
1 = E[X] = var(X) = 2 3 = 0 4 = 34
Median and mode equal to

52. Exponential families
Class of parametric densities with nice analytic properties
Start from the normal density:
'(x; ) =
1
p
2
exp
x - x2=2 - 2=2
=
expf-2=2g
p
2
exp fxg exp
-x2=2
where and x only interact through single exponential product

53. Exponential families
Class of parametric densities with nice analytic properties
De

54. nition
A parametric family of distributions on X is an exponential family
if its density with respect to a measure satis

55. es
f(xj) = c()h(x) expfT(x)T()g , 2 ,
where T() and () are k-dimensional functions and c() and h()
are positive unidimensional functions.
Function c() is redundant, being de

56. ned by normalising constraint:
c()-1 =
Z
X
h(x) expfT(x)T()gd(x) .

57. Exponential families (examples)
Example 1: Binomial experiment again
Binomial variable
X B(n, p) P(X = k) =
n
k
pk(1 - p)n-k
can be expressed as
P(X = k) = (1 - p)n
n
k
expfk log(p=(1 - p))g
hence
c(p) = (1 - p)n , h(x) =
n
x
, T(x) = x , (p) = log(p=(1 - p))

58. Exponential families (examples)
Example 2: Normal experiment again
Normal variate
X N(, 2)
with parameter = (, 2) and density
f(xj) =
1
p
22
expf-(x - )2=22g
=
1
p
22
expf-x2=22 + x=2 - 2=22g
=
expf-2=22g
p
22
expf-x2=22 + x=2g
hence
c() =
expf-2=22g
p
22
, T(x) =
x2
x
, () =
-1=22
=2

59. natural exponential families
reparameterisation induced by the shape of the density:
De

60. nition
In an exponential family, the natural parameter is () and the
natural parameter space is
=

61. 2 Rk;
Z
X
h(x) expfT(x)Tgd(x) 1
Example For the B(m, p) distribution, the natural parameter is
= logfp=(1 - p)g
and the natural parameter space is R

62. natural exponential families
reparameterisation induced by the shape of the density:
De

63. nition
In an exponential family, the natural parameter is () and the
natural parameter space is
=

64. 2 Rk;
Z
X
h(x) expfT(x)Tgd(x) 1
Example For the B(m, p) distribution, the natural parameter is
= logfp=(1 - p)g
and the natural parameter space is R

65. regular and minimal exponential families
Possible to add/delete useless components of T:
De

66. nition
A regular exponential family corresponds to the case where is an
open set. A minimal exponential family corresponds to the case
when the Ti(X)'s are linearly independent, i.e.
P(TT(X) = const.) = 0 for 6= 0
Also called non-degenerate exponential family
Usual assumption when working with exponential families

67. regular and minimal exponential families
Possible to add/delete useless components of T:
De

68. nition
A regular exponential family corresponds to the case where is an
open set. A minimal exponential family corresponds to the case
when the Ti(X)'s are linearly independent, i.e.
P(TT(X) = const.) = 0 for 6= 0
Also called non-degenerate exponential family
Usual assumption when working with exponential families

69. Illustrations
For a Normal N(, 2) distribution,
f(xj, ) =
1
p
2
1
expf-x2=22 + =2 x - 2=22g
means this is a two-dimensional minimal exponential family
For a fourth-power distribution
f(xj) = C expf-(x - )4gg / e-x4
e43x-62x2+4x3-4
implies this is a three-power distribution
[Exercise:

70. nd C]

71. convexity properties
Highly regular densities
Theorem
The natural parameter space of an exponential family is convex
and the inverse normalising constant c-1() is a convex function.
Example For B(n, p), the natural parameter space is R and the
inverse normalising constant (1 + exp())n is convex

72. convexity properties
Highly regular densities
Theorem
The natural parameter space of an exponential family is convex
and the inverse normalising constant c-1() is a convex function.
Example For B(n, p), the natural parameter space is R and the
inverse normalising constant (1 + exp())n is convex

73. analytic properties
Lemma
If the density of X has the minimal representation
f(xj) = c()h(x) expfT(x)Tg
then the natural statistic T(X) is also from an exponential family
and there exists a measure T such that the density of T(X)
against T is
c() expftTg

74. analytic properties
Theorem
If the density of T(X) against T is c() expftTg, if the real value
function ' is measurable with
Z
j'(t)j expftTg dT (t) 1
on the interior of , then
f : !
Z
'(t) expftTg dT (t)
is an analytic function on the interior of and
rf() =
Z
t'(t) expftTg dT (t)

75. analytic properties
Theorem
If the density of T(X) against T is c() expftTg, if the real value
function ' is measurable with
Z
j'(t)j expftTg dT (t) 1
on the interior of , then
f : !
Z
'(t) expftTg dT (t)
is an analytic function on the interior of and
rf() =
Z
t'(t) expftTg dT (t)
Example For B(n, p), the natural parameter space is R and the
inverse normalising constant (1 + exp())n is convex

76. moments of exponential families
Normalising constant c() inducing all moments
Proposition
If T(x) 2 Rd and the density of T(X) is expfT(x)T - ()g, then
E
expfT(x)Tug
= expf ( + u) - ()g
and () is the cumulant generating function.

77. moments of exponential families
Normalising constant c() inducing all moments
Proposition
If T(x) 2 Rd and the density of T(X) is expfT(x)T - ()g, then
E[Ti(x)] =
@ ()
@i
i = 1, . . . , d,
and
E
cov(Ti(X), Tj(X))
=
@2 ()
@i@j
i, j = 1, . . . , d
Sort of integration by part in parameter space:
Z

78. Ti() +
@
@i
c()h(x) expfT(x)Tgd(x) =
log c()
@
@i
1 = 0

79. further examples of exponential families
Example
Chi-square 2
k distribution corresponing to distribution of
X21
+ . . . + X2
k when Xi N(0, 1), with density
fk(z) =
zk=2-1 expf-z=2g
2k=2 (k=2)
z 2 R+

80. further examples of exponential families
Counter-Example
Non-central chi-square 2
k() distribution corresponing to
distribution of X21
+ . . . + X2
k when Xi N(, 1), with density
fk,(z) = 1=2 (z=)k=4-1=2 expf-(z + )=2gIk=2-1(
p
z) z 2 R+
where = k2 and I Bessel function of second order

81. further examples of exponential families
Counter-Example
Fisher Fn,m distribution corresponding to the ratio
Z =
Yn=n
Ym=m
n, Ym 2
m ,
Yn 2
with density
fm,n(z) =
(n=m)n=2
B(n=2,m=2)
zn=2-1 (1 + n=mz)-n+m=2

82. further examples of exponential families
Example
Ising Be(n=2,m=2) distribution corresponding to the distribution of
Z =
nY
nY +m
when Y Fn,m
has density
fm,n(z) =
1
B(n=2,m=2)
zn=2-1 (1 - z)m=2-1 z 2 (0, 1)