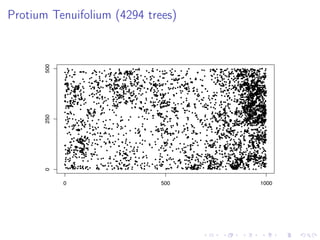
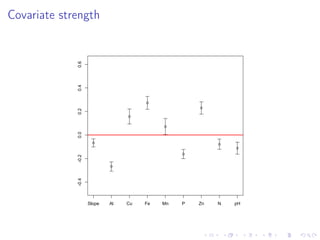
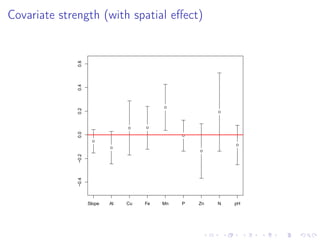
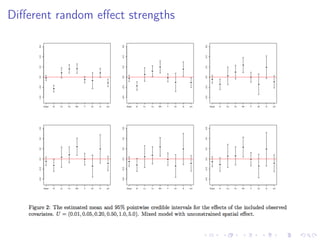
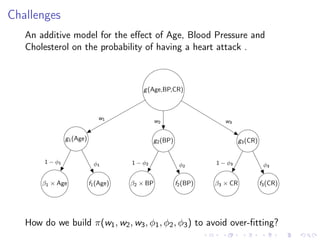
The document discusses the complexities and challenges of modeling large datasets, particularly in ecological contexts, emphasizing the necessity of investment in both modeling and computational strategies to address uncertainties. It illustrates specific examples involving fish population surveys and whale pod observations to demonstrate statistical questions related to detection probabilities and inference in the presence of noise and incomplete data. Furthermore, the text highlights the limitations and nuances of Gaussian processes in modeling non-linear effects, advocating for Bayesian approaches to enhance interpretability and manage uncertainty in ecological modeling.

1. To avoid fainting, keep repeating “It’s only a
model”...
Daniel Simpson
Department of Mathematical Sciences
University of Bath

2. Outline
Amuse-bouche
What is this? A model for ants?!
Moisture is the essence of wetness, and wetness is the essence of beauty.
With low power comes great responsibility
Miss Jackson if you’re nasty
The Ganzfeld effect

3. “We are tied down to a language which makes up in
obscurity what it lacks in style.”
Never mind the big data, here come the big models

4. “Eternity is a terrible thought. I mean, where’s it going to
end?”
Folk definition
A model becomes big when the methods I want to use no longer
work.
Solving “big models” require investment in modelling (priors
and likelihoods).
Solving “big models” require investment in computation
(scalable, tailored solutions).
Solving “big models” requires compromise (exactness isn’t an
option).

5. “We’re more of the love, blood, and rhetoric school”
Question for the ages
Is my model really “big” if it only has one infinite dimensional
parameter?
I spend a lot of effort trying to convince myself that my
models aren’t too big
Most of the games that I play are with space, time, or some
horrid combination of the two
I am addicted to GAMs
I was once at a party where all the cool kids were doing inverse
problems. I swear I didn’t inhale.

6. Outline
Amuse-bouche
What is this? A model for ants?!
Moisture is the essence of wetness, and wetness is the essence of beauty.
With low power comes great responsibility
Miss Jackson if you’re nasty
The Ganzfeld effect

7. An archipelago off the coast of Finland
(with Haakon Bakka, Håvard Rue, and Jarno Vanhatalo)
Smelt (other: herring, perch, pike
perch)
Commercially important fish species
Survey data on fish larvae
abundance
Complex models, high uncertainty

8. An archipelago off the coast of Finland
200 400 600 800 1000 1200 1400 1600
20040060080010001200
x
y
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q q
q
q
q
q
q
q
q
q
q
q
q
q q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q

9. I’ll tell you what I want (what I really really want)
The questions for this dataset revolve around conservation. (e.g.
should we protect some regions?)
Statistical questions
“Interpolation” (where are the smelt?)
“Extrapolation” (where would we expect the smelt to be in a
similar, but different environment)
Model the nonlinear effect of environmental variables.
(scenario forecasts)

10. Outline
Amuse-bouche
What is this? A model for ants?!
Moisture is the essence of wetness, and wetness is the essence of beauty.
With low power comes great responsibility
Miss Jackson if you’re nasty
The Ganzfeld effect

11. What’s a homophone between friends?
Antisocial behaviour in Wales. Social behaviour in whales.

12. It’s kinda like a point pattern...
(Finn Lindgren, Fabian Bachl, Joyce Yuan, David Borchers, Janine Illian)
You can treat whale pods as a point process
Partially observed along transects (unknown detection
probability!)
Each observed pod has an noisy measurement of size

13. Gimme! Gimme! Gimme! (A man after midnight)
(I’d already used the Spice Girls one...)
The scientific questions are “How many whales are there?” and
“Where are they?”.
Statistical questions:
How do you estimate the detection probability?
How do you do inference with a filtered point process?
How do you deal with error in the mark observation?

14. Outline
Amuse-bouche
What is this? A model for ants?!
Moisture is the essence of wetness, and wetness is the essence of beauty.
With low power comes great responsibility
Miss Jackson if you’re nasty
The Ganzfeld effect

15. Like any good academic statistician, I will now present the
abstract problem
(And never return to the interesting one)
Observed field
yi ∼ π(yi | η, θ)
Latent field
η ∼ N(0, Q−1
)
Parameters
θ ∼ π(θ)
{yi }N
i=1 can be
non-Gaussian,
multivariate, etc.
θ contains any
non-Gaussian paramter
η ∈ Rn contains
everything that is jointly
Gaussian.
Big N = “Big Data”. Big n = “Big Model”

16. How do we control the chaos?
Eight out of Ten* dentists
recommend using Bayes to
perform meaningful inference
on your big model!
* indicates prior belief. May conflict with data.

17. “My n is ∞!” “Well my n is eight times ∞!”
It is not hard to make your model big.
Each non-linear component in a GAM is infinite dimensional
Every spatial or spatio-temporal GRF is infinite dimensional
Random effects, and “region” effects add up...
A vital point
Any prior π(η | θ) adds an enormous amount of information.

18. “The word "optimal" brings a lot of dreary baggage that
these authors may be too young to remember and would do
well to avoid.”
A toy problem is GP regression
yi ∼ N(x(si ), 1).
{si }n
i=1 known
Unknown function x(·) taken a priori to be a Gaussian Process
(GP), i.e.
(x(s1), x(s2), . . . , x(sn))T
∼ N(0, Σ)
Covariance matrix Σij = kθ(si , sj )
Result
If the GP prior represents a genuine and correct a priori belief about
the smoothness of the true function x0(·), estimators based on the
posterior will be asymptotically optimal.

19. “The word "optimal" brings a lot of dreary baggage that
these authors may be too young to remember and would do
well to avoid.”
A toy problem is GP regression
yi ∼ N(x(si ), 1).
{si }n
i=1 known
Unknown function x(·) taken a priori to be a Gaussian Process
(GP), i.e.
(x(s1), x(s2), . . . , x(sn))T
∼ N(0, Σ)
Covariance matrix Σij = kθ(si , sj )
Result
If the GP prior represents a genuine and correct a priori belief about
the smoothness of the true function x0(·), estimators based on the
posterior will be asymptotically optimal.

20. “except as a source of approximations [...] asymptotics have
no practical utility at best and are misleading at worst”
So to make the asymptotics work as we get more data, we
need to specify the GP smoothness correctly
Awkward!
A work around: Choose a very smooth GP e.g.
k(s, t) = exp(−κ(s − t)2
)
and put a good prior on κ. (van der Vaart & van Zanten,
2009)
Bayes to the rescue!

21. Smooth operator
There’s a small problem...
Computing the prior density requires the calculation of
xT Σ−1
x
Observation: f T
Σg ≈ f (s) K(s, t)g(t) dt ds
So Σ “is” the discrete version of the integral operator with
kernel K(·, ·).
So the eigenvalues of Σ are going to be related to the
power-spectrum of x(·) (i.e. the Fourier transform of K(0, t))

22. Just Dropped In (To See What Condition My Condition
Was In)
Result (Shaback, 1995)
cond2(Σ) = O(hd exp(kd2/h2),
h is the minimum separation between two points in the design.
d is the dimension of s (take it to be 1)
By the usual interpretation of the condition number, we lose
O(h−2) digits of accuracy every time we compute xT Σ−1
x
We can think of this as an uncertainty principle. As we get
more statistically accurate, we are unable to compute the
solution.
Note: Things are better for the posterior covariance matrix
under Gaussian observations. But you have to be very very
careful!

23. I want you, but I don’t need you
So we hit a snag with being optimal... But it’s not entirely
catastrophic
Use lower smoothness (better conditioning)
or use a different basis
or, ask a question: what’s breaking my big model?
Where it all went wrong
The problems come in resolving the high-frequency behaviour. Do
we care about this?

24. Just nip the tip
Replace x(·) with xn(·) = n
i=1 xi φi (·), x ∼ N(0, Σn)
Fourier basis (truncated Karhunen-Loéve expansion)
Wavelets
Piecewise polynomials.

25. Piecewise linear approximation of surfaces
NB: The basis functions are only non-zero on a small part of the
domain.

26. “Which is a kind of integrity, if you look on every exit being
an entrance somewhere else.”
Result
The error in posterior functionals induced by using a
finite-dimensional basis instead of a GP of optimal smoothness is of
the same order as the approximation error
Sometimes our big models are bigger than we need
By using a finite basis, we separate the world into things we
care about and things we don’t
We trade (asymptotic) bias for robustness against
mis-specification
(We still need to watch the conditioning, though)

27. Outline
Amuse-bouche
What is this? A model for ants?!
Moisture is the essence of wetness, and wetness is the essence of beauty.
With low power comes great responsibility
Miss Jackson if you’re nasty
The Ganzfeld effect

28. No Repliates, Mo’ Problems
Presence only data occurs frequently in ecology
Simplest question to ask: How does covariate (xxx) change
the local risk of a sighting?
Basically, is a covariate effect “significant”?
One big problem: No possibility of replicates.

29. Protium Tenuifolium (4294 trees)
0 500 1000
0250500

30. A useful example: Log-Gaussian Cox processes
The likelihood in the most boring case is
log(π(Y |x(s))) = |Ω| −
Ω
Λ(s) ds +
si ∈Y
Λ(si ),
where Y is the set of observed locations and Λ(s) = exp(x(s)), and
x(s) is a Gaussian random field.
The is very different from the Gaussian examples: it requires the
field everywhere!

31. If you liked it then you should’ve put a grid on it

32. An approximate likelihood
NB: The number of points in a region R is Poisson distributed with
mean R Λ(s) ds.
Divide the ‘observation
window’ into rectangles.
Let yi be the number of
points in rectangle i.
yi |xi , θ ∼ Po(exi
),
The log-risk surface is
replaced with
x|θ ∼ N(µ(θ), Σ(θ)).
Introduction Case study I Case study II Summary Resolution Spatial e↵ect Interaction Estima
Andersonia heterophylla: 55 ⇥ 55 grid
●
●
●
●
●
●
●●
●●●
● ●●
●
●
●●
●● ●
●
●●
●
●●●
● ●●
●
●
●●●
●
●
● ●
●
●
● ●
●●
●●●●
● ●
●●
● ●●●
●
●
●●
●●
●●
●● ●
●●
●●
●●
●
●
●
●●
● ●● ●●
●●●
●●●
●
●●
●
●
●
●●
●● ● ●●
●●●●
●
●●
●●
●
●
●● ●●
●
●
●
●
●
●●
●
●
●
●
● ●●
●●
●●●● ●●
●● ●
●
●
●● ●●●●●
●●●
●
●
●●
●●●
●●
●●
● ●
●● ●●
●●● ●● ●
●●
●●
●
● ●● ●●●
●
●
●●●
●
●
●
●●
●●
●●●
●
●●● ●
●●●
●
●
●
● ●●●
●●●
●● ●● ●
●●
●●
●
●
●●
●●●
●
●
●●
●● ●●
●
●
●
●
●● ●
●
●● ●● ●●
●
●●
●
● ● ●●
●
●
●
●●●
●
●●
● ●● ●●
●
●● ●●
●●●●● ●
●● ●●
●●
●
●●● ●
●
●
●●
●
●
●
●● ●●● ●
●
●
●
●
●
● ●● ●
●
●
●● ●●
●●●
●●
●●●
●●
●
● ●● ●
●
● ●
●●
●
●
●●
●● ●●●
●●
●
●
●
●
●
●
●
●
●
●
●●
●●
●●
● ●●● ●●
●
● ●
●● ●● ●
● ●
● ● ●●● ● ●● ●●●
●
● ●
●
●
●
●
●●
●
● ●●●
● ●●
●
●●
●
●
●
●● ●
● ●
●
●
●
●
●
●●
●●
●
● ●● ●●● ● ●●●● ●● ●●● ●● ●● ●●●● ●●● ●● ●● ●●●●● ●● ●● ●●●●●● ●●●●● ●●● ●●●● ●●●●● ●● ●● ● ●●●● ●●●● ●●●●● ●●●● ●●●●●● ●●● ●●● ●●●●●●● ●●●●● ●●● ●●●●● ●●●●● ●●●●●● ●●●●●● ●●●●●● ●●● ●●●●●● ●●●● ●●●●●● ●●● ●● ●●●● ●●●● ●●●● ●●● ●●●●● ●●● ●●●● ● ●●●●●●● ●●●●●● ●●●●●● ●● ●●●●● ●●●●●●● ●●● ●●●● ●●●●●●●● ●●●●
Sigrunn Holbek Sørbye, University of Tromsø Spatial point patterns - simple case studies

33. But does this lead to valid inference?
Yes—we have perturbation bounds.
Loosely, the error in the likelihood is transferred exactly (order
of magnitude) to the Hellinger distance between the true
posterior and the computed posterior.
This is conditional on parameters.
For the LGCP example, it follows that, for smooth enough
fields x(s), the error is O(n−1)
The approximation turns an impossible problem into a difficult, but
still useful, problem.

34. Covariate strength
-0.4-0.20.00.20.40.6
Slope Al Cu Fe Mn P Zn N pH

35. Covariate strength (with spatial effect)
q
q
q q
q
q
q
q
q
−0.4−0.20.00.20.40.6
q
q
q q
q
q
q
q
q
Slope Al Cu Fe Mn P Zn N pH

36. Oh dear!
Adding a spatial random effect, which accounts for
“un-modelled covariates” massively changes the scientific
conclusions
One solution: Make spatial effect orthogonal to covariates
Pro: Cannot “steal” significance
Cons: Interpretability, Poor coverage
This is basically the “maximal covariate effect”
Without replicates, we cannot calibrate the smoothing
parameter to get coverage.

37. Subjective Bayes to the rescue!
Key idea: If we can interpret the model, we can talk about the
credible intervals as updates of knowledge
The random field has two parameters: one controlling the
range (unimportant) and one controlling the in-cell variance
(IMPORTANT!)
A prior the variance can be constructed such that
Pr(std(xi ) > U) < α
Changing U changes interpretation
The effect of Aluminium is significantly negative
when U < 1, but the credible crosses zero for all
U > 1.
We can relate U to the “degrees of freedom”...

38. Subjective Bayes to the rescue!
Key idea: If we can interpret the model, we can talk about the
credible intervals as updates of knowledge
The random field has two parameters: one controlling the
range (unimportant) and one controlling the in-cell variance
(IMPORTANT!)
A prior the variance can be constructed such that
Pr(std(xi ) > U) < α
Changing U changes interpretation
The effect of Aluminium is significantly negative
when U < 1, but the credible crosses zero for all
U > 1.
We can relate U to the “degrees of freedom”...

39. Subjective Bayes to the rescue!
Key idea: If we can interpret the model, we can talk about the
credible intervals as updates of knowledge
The random field has two parameters: one controlling the
range (unimportant) and one controlling the in-cell variance
(IMPORTANT!)
A prior the variance can be constructed such that
Pr(std(xi ) > U) < α
Changing U changes interpretation
The effect of Aluminium is significantly negative
when U < 1, but the credible crosses zero for all
U > 1.
We can relate U to the “degrees of freedom”...

40. Subjective Bayes to the rescue!
Key idea: If we can interpret the model, we can talk about the
credible intervals as updates of knowledge
The random field has two parameters: one controlling the
range (unimportant) and one controlling the in-cell variance
(IMPORTANT!)
A prior the variance can be constructed such that
Pr(std(xi ) > U) < α
Changing U changes interpretation
The effect of Aluminium is significantly negative
when U < 1, but the credible crosses zero for all
U > 1.
We can relate U to the “degrees of freedom”...

41. Subjective Bayes to the rescue!
Key idea: If we can interpret the model, we can talk about the
credible intervals as updates of knowledge
The random field has two parameters: one controlling the
range (unimportant) and one controlling the in-cell variance
(IMPORTANT!)
A prior the variance can be constructed such that
Pr(std(xi ) > U) < α
Changing U changes interpretation
The effect of Aluminium is significantly negative
when U < 1, but the credible crosses zero for all
U > 1.
We can relate U to the “degrees of freedom”...

42. Subjective Bayes to the rescue!
Key idea: If we can interpret the model, we can talk about the
credible intervals as updates of knowledge
The random field has two parameters: one controlling the
range (unimportant) and one controlling the in-cell variance
(IMPORTANT!)
A prior the variance can be constructed such that
Pr(std(xi ) > U) < α
Changing U changes interpretation
The effect of Aluminium is significantly negative
when U < 1, but the credible crosses zero for all
U > 1.
We can relate U to the “degrees of freedom”...

43. Different random effect strengths

44. Advantages
Once again, an interpretable prior allows us to control our
inference in a sensible way
We can talk about updating knowledge
Explicitly conditioning on the prior allows us to communicate
modelling assumptions
Interpretation without appeals to asymptotics (but well
behaved if more observations come)
Prior and interpretation can/should be made independent of
the lattice

45. Disadvantages

46. Challenges
An additive model for the effect of Age, Blood Pressure and
Cholesterol on the probability of having a heart attack .
β1 × Age f1(Age)
g1(Age)
1 − φ1 φ1
β2 × BP f2(BP)
g2(BP)
1 − φ2 φ2
β3 × CR f3(CR)
g3(CR)
1 − φ3 φ3
g(Age,BP,CR)
w1
w2 w3
How do we build π(w1, w2, w3, φ1, φ2, φ3) to avoid over-fitting?

47. Outline
Amuse-bouche
What is this? A model for ants?!
Moisture is the essence of wetness, and wetness is the essence of beauty.
With low power comes great responsibility
Miss Jackson if you’re nasty
The Ganzfeld effect

48. You gotta get a gimmick
A Savage Quotation
You should build your model as big as an elephant
A von Neumann quote
With four parameters I can fit an elephant, and with five I can
make him wiggle his trunk.

49. Placating pugilistic pachyderms
Priors that Penalise Complexity Prevent Poor Performance
Under everything, this was a talk about
setting prior distributions
This is hard.
This is even harder for big models
We must constantly guard against the
Ganzfeld effect
While being flexible enough to find things
that are there
Big models are more than just a
computational challenge, they require a
great deal of new investment in our
modelling infrastructure.
Mayer, Khairy, and
Howard,
Am. J. Phys. 78,
648 (2010)

50. References
D. P. Simpson, H. Rue, T. G. Martins, A. Riebler, and S. H.
Sørbye (2014) Penalising model component complexity: A
principled, practical approach to constructing priors.
arxiv:1403.4630
D. P. Simpson, J. Illian, F. K. Lindgren, S. H. Sørbye, and
H. Rue (2015) Going off grid: Computationally efficient
inference for log-Gaussian Cox processes. Biometrika,
Forthcoming. (arXiv:1111.0641)
Geir-Arne Fuglstad, Daniel Simpson, Finn Lindgren, and
Håvard Rue (2015) Interpretable Priors for Hyperparameters
for Gaussian Random Fields. arXiv:15xx:xxx.