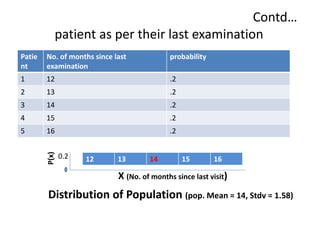
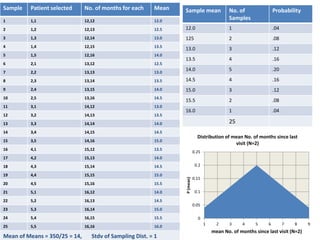
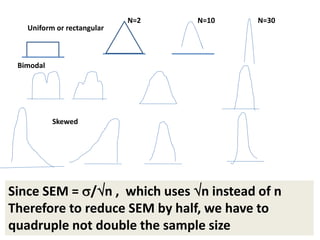
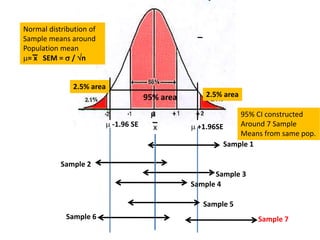
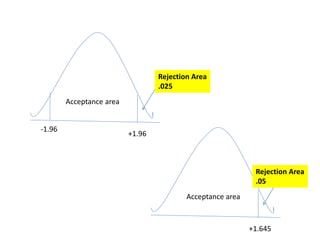
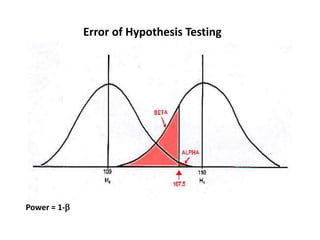
This document discusses sampling distributions and their use in making statistical inferences from data. It begins by defining key aspects of sampling distributions, including the statistic of interest (e.g. mean, proportion), random selection of samples, sample size, and population. It then generates a sampling distribution using an example of calculating the mean number of months since patients' last medical examination across different samples. The document outlines important characteristics of sampling distributions and how the central limit theorem applies. It also discusses how to construct confidence intervals and conduct hypothesis testing using sampling distributions.

1. Making Inferences from Data:
Confidence Interval & Hypothesis Testing
Dr. Amita Kashyap
Sr. Prof. Community Medicine
S.M.S. Med. College, Jaipur

2. Sampling Distribution
• Four features define a sampling distribution
– Statistic of interest i.e. mean, standard deviation,
or proportion
– Random selection of sample
– Size of random sample
– Specification of population being sampled

3. Generating a sampling Distribution
• Example- suppose a physician wants to decide
if he should mail reminders for annual
examination to his patients?
• He examine files of his patients and
determines how many months has passed
since last examination
• Lets assume total population of patients is 5
• We select all possible samples of 2 patients
per sample and calculate mean No. of months

4. Contd…
patient as per their last examination
Patie
nt
No. of months since last
examination
probability
1 12 .2
2 13 .2
3 14 .2
4 15 .2
5 16 .2
12 13 14 15 16
0.2
P(x)
X (No. of months since last visit)
Distribution of Population (pop. Mean = 14, Stdv = 1.58)

5. Sample Patient selected No. of months for each Mean
1 1,1 12,12 12.0
2 1,2 12,13 12.5
3 1,3 12,14 13.0
4 1,4 12,15 13.5
5 1,5 12,16 14.0
6 2,1 13,12 12.5
7 2,2 13,13 13.0
8 2,3 13,14 13.5
9 2,4 13,15 14.0
10 2,5 13,16 14.5
11 3,1 14,12 13.0
12 3,2 14,13 13.5
13 3,3 14,14 14.0
14 3,4 14,15 14.5
15 3,5 14,16 15.0
16 4,1 15,12 13.5
17 4,2 15,13 14.0
18 4,3 15,14 14.5
19 4,4 15,15 15.0
20 4,5 15,16 15.5
21 5,1 16,12 14.0
22 5,2 16,13 14.5
23 5,3 16,14 15.0
24 5,4 16,15 15.5
25 5,5 16,16 16.0
Mean of Means = 350/25 = 14, Stdv of Sampling Dist. = 1
Sample mean No. of
Samples
Probability
12.0 1 .04
125 2 .08
13.0 3 .12
13.5 4 .16
14.0 5 .20
14.5 4 .16
15.0 3 .12
15.5 2 .08
16.0 1 .04
25
0
0.05
0.1
0.15
0.2
0.25
1 2 3 4 5 6 7 8 9
P
(mean)
mean No. of months since last visit (N=2)
Distribution of mean No. of months since last
visit (N=2)

6. Important characteristics of Sampling Distribution
• The mean of 25 separate means is 14 , same
as population mean
• The variability in the sampling distribution is
less than the variability in original population
(Stdv of pop.= 1.58 while of sampling distribution it is 1)
• Shape of sampling distribution of means, even
for a sample of size 2, is beginning to
approach the shape of normal distribution
although the shape of the original population
is rectangular not normal!

7. Central Limit Theorem
• The mean of sampling distribution is equal to the
population mean  (based on individual observations)
• The standard deviation in the sampling
distribution of mean (SDM) is equal to /n
(SEM)
• If the distribution of original population is normal
then the SDM is also normal,
• More importantly, for sufficiently large sample
size, the SDM is approximately normally
distributed, regardless of the shape of original
population distribution

8. Uniform or rectangular
Bimodal
Skewed
N=2 N=10 N=30
Since SEM = /n , which uses n instead of n
Therefore to reduce SEM by half, we have to
quadruple not double the sample size

9. Summing up
• In actual practice, selecting repeated
samples of size ‘N’ and generating sampling
distribution is not necessary.
• Instead, one sample is selected, sample
mean is calculated as an estimate of the
population mean and if the sample size is
≥30 CLT is invoked to argue that the SDM is
known

10. Standard deviation vs SE
• The value of  measures the St.Dev of
individual values in the population (i.e.
how much variability can be expected
among individuals)
• SE of the mean, however, is the St.Dev of
the mean in a sampling distribution (i.e.
how much variability can be expected in
future sample means)

11. Standard deviation vs SE
• SE is a function of sample, so it can be
made smaller simply by increasing ‘N’.
• Secondly the interval ‘mean2SE’ will
contain approximately 95% of the means
of samples but it will never contain 95%
of the observations on individuals

12. Other sampling distributions (SD)..
• Statistic other than the mean also have
sampling distributions
• SD for, median, proportions and correlation
• In each case statistical issue is the same-
“how can the statistic of interest be
expected to vary across different samples
of same SS”
• Although SDM is normally distributed, SD of
most other statistics are not

13. ..Other sampling distributions…
• In fact SDM assumes that the value of  is
known
• In actuality it is rarely known and is
estimated by sample StDev ‘s’ and SE /n
by s/n
• The SDM with an estimated StDev actually
follows a ‘t’ distribution instead
• The SD of the two variances follows ‘F’
Distribution

14. …Other sampling distributions
• The proportion, which is based on the
binomial distribution, is normally
distributed under certain circumstances
• For the correlation to follow the normal
distribution, a transformation must be
applied
• One property that all distributions have
in common is having a SE

15. Application using SDM…
• Critical ratio(z score) transforms a
normally distributed random variable
with mean ‘’ & St.Dev ‘’ to the
standard normal (z) distribution with
mean ‘0’ and St.Dev ‘1’ z= x- / 
• When we are interested in mean rather
than individual observations, it is the
mean which is transformed

16. …Application using SDM
• According to CLT, the mean of SM is ‘’
but the St.Dev (SEM) is ‘/n’
• Therefore the critical ratio that transform
a mean to have a distribution with mean
‘0’ and St.Dev ‘1’
x- 
 /n
z=

17. Example of use of the critical ratio – ‘z’
• A physician studies a randomly selected group of 25 men
& women between 20-39 yrs of age and finds their mean
systolic BP is 124 mm Hg. How often would a sample of
25 patients have a mean systolic BP this high or higher?
• We assume that systolic BP is normally distributed
random variable with a known mean of 120 mm Hg. And
a St.Dev of 10 mm Hg in the population of normal
healthy adults
124- 120
10 /25
z= = 4/2= 2.0
The proportion of the z distribution area above 2 is 0.023,
therefore 2.3% of random samples with n=25 can be
expected to have A mean systolic BP of 124 mm Hg or higher

18. • Suppose a physician wants to detect adverse
effects on systolic BP in random sample of 25
patients using a drug that causes
vasoconstriction.
• He decides that a mean systolic BP in the upper
5% of the distribution is cause of alarm, so what
value of systolic BP should alarm him?
x- 120
10 /25
1.645= x- 120/2 i.e. 1.645X 2+120 =x = 123.29
123.29 mm of Hg is the value that divides
the SDM into the lower 95% and upper
5% so there is cause for alarm if the
mean in the sample surpasses this value

19. • Continuing with examples 1 and 2, to know how
many patients should be included in the study so
that 90% of times sample mean is 122 or less.
1.28=
122- 120
10 /n
i.e. 1.28=2 n/10
i.e. n=6.40
n=6.402 = 40.96 = 41
Ex. 4 .
In normal healthy adults PO2 has a mean of
90 mmHg with a StDev of 7.
What proportion of individuals can be expected
to have PO2 between 83-97 mm Hg
(assume PO2 has normal distribution)

20. Ctd…
• Z= X - / (/ )= 83-90/ 7 = -7/7 = -1,
• Z= X - /( / ) = 97-90/ 7 = 7/7= 1,
• The proportion of the area between  1 z =
0.683, therefore 68.3% of Normal healthy
individuals are expected to have PO2 between
83-97 mm Hg

21. Ex. 5
• If repeated samples of 6 healthy individuals are
randomly selected what proportion will have
mean between 83-97 mm Hg?
• This Q. concerns means not individuals, so the
critical ratio for means must be used to find
appropriate area under the curve
• Z = X - / ( n) = 83-90/ (7/6) = -7/2.5= -2.5,
• Z = X - / ( n) = 97-90/ (7/  6) = 7/2.5= +2.5,
• the area btw 2.5 z = 0.988, therefore 98.8% 0f
the mean PO2 values of future samples of 6
patients will fall between 83-97 mm Hg

22. Approaches for statistical inference:
• Estimating parameters – the process of
using information from a random sample
to draw conclusions about the value of a
population parameter.
• Testing Hypothesis – testing a statement
of belief about population parameter

23. Estimation
• Suppose we want to evaluate the impact of
toxic reaction of drugs on falls resulting
fractures among elderly patients
• For logistic and economic reasons, we just do
a cohort study with a random, representative
sample of elderly patients followed for a
specified period of time
• The proportion (p)of patients in the sample
who experience drug reaction and fractures
can be determined and used as an estimate
for the proportion of drug reaction and
fractures in the population

24. ctd…..
• We may be interested in mean rather
than proportion in some other studies
eg. Mean wt loss after a particular diet!
• Both p and X are point estimates for P
and , other point estimates are the
sample StDev for  and sample Corr. For
pop. Corr.

25. • Characteristics of a good estimator:-
–Un-biasedness – when x of the sample
statistic = 
–Efficiency – for a given sample size the SE of
the sample statistic is as small as possible
–Consistent - if its value approaches that of
population parameter as the sample size
increases
• However, point estimates are nearly always
different than population parameter.

26. Ctd….
• Mean of randomly selected samples are good
estimator of  but we know that it is subject
to sampling error
• Mean of sampling distribution is =  but not
Mean of individual sample
• For this reason, interval estimates, which
specify a range of values (CI), are often used
instead of point estimates

27. Confidence interval and Confidence Limits
• Interval estimates or confidence
intervals define an upper and a lower
limit with an associated probability, the
ends of confidence interval are called
confidence limits
• The probability that a specified interval
contains the unknown population
parameter is called confidence

28. 95% area
 -1.96 SE  +1.96SE
2.5% area
2.5% area

x
Sample 1
Sample 2
Sample 3
Sample 4
Sample 5
Sample 6 Sample 7
95% CI constructed
Around 7 Sample
Means from same pop.
Normal distribution of
Sample means around
Population mean
= x SEM =  / n

29. • CI for  = sample mean  a sampling error
• The actual allowance for sampling error is computed by taking
an appropriate number of SE according to how confident we
wish to be that our interval estimate will in fact include the
true .
• It is common to choose 95% confidence level, i.e. an interval
such that there is 95% chance that it will contain 
• From SDM we can say that 95% CI for  = X1.96 SE
• Level of confidence other than 95% may be obtained simply
by substituting appropriate value of the ‘standard normal
variable-Z’ . The desired level of confidence may be denoted
as 100(1-) percent .
• Thus for 95% confidence  = 0.05 and the area in each tail is
given by /2 (i.e. 0.025)
• CI for  using z values CI= x  Z/2 SEM
• Z/2 denotes the value of Z that cuts off an area of /2 in each tail

30. Example for interpreting CI
• In a study investigator found mean level of alcohol
consumption in 142 men with psoriasis as 42.9 gm/ day
with StDev 85.8 as opposed to mean consumption of
21.0 gm/day with 34.2 StDev. in population without
psoriasis (other skin disease patients without psoriasis ).
• How precise is this estimate of mean alcohol intake in
psoriasis patients, i.e. what variability they can find in
other similar groups of psoriasis patients ?
• CI= x  Z/2 SEM = 42.9-1.96 X (85.8/142)
42.9+1.96 X (85.8/142)
= 28.8 – 57.0 gm / day
Exercise – calculate 90% and 99% CI for this

31. Hypothesis Testing
• Purpose again is to permit generalization
• Both statistical hypothesis testing and
estimation make certain assumption about
the population and then use probabilities to
estimate the likelihood of the results and both
assume a random sample has been taken
• The investigators of previous study could have
stated the question as : “on the average, do
men with psoriasis drink the same amount of
alcohol daily as men with skin diseases other
than psoriasis?”

32. • In hypothesis testing we first assume that there is
no difference ie. Men with psoriasis consume
alcohol same as men without it (i.e 21gm/day in
this investigation)
• And then we determine the probability of
observing an intake equal to 42.9 gm/day in a
group of 142 men given this assumption
• If probability is large, we conclude that the
assumption is justified and that both groups
consume similar amount of alcohol, but
• If probability is small, such as 1 in 20 (0.05) or 1 in
100 (0.01) – we conclude that the assumption is
not justified and there is a real difference!

33. Steps in testing statistical Hypothesis
Step 1:
• State the research question in terms of Statistical
Hypothesis:
– Null Hypothesis – H0 states no difference btw
assumed or hypothesized value and population mean
– Alternative Hypothesis H1 – states disagreement with
H0
– If there is no sufficient evidence to reject the null
hypothesis it is stated as Null Hypothesis “not
rejected” rather then “Accepted”

34. For our investigation
• Ho:  = 21 gm / day (the mean in the pop. is 21gm/day)
• H1 :   21 gm / day (the mean in the pop. is not 21gm/day)
• These hypothesis results in a two tailed (non directional) test.
• One tailed (directional) test occurs when investigators do have an priori
expectation – want to test whether it is larger or smaller than the
population mean
• One tailed Alternative Hypothesis is : H1 :  <21 gm / day or H1 :  > 21
gm / day
• Note that it is the Alternative Hypothesis that indicates whether a test
is one tailed or two tailed
• Advantage of one tailed test is that statistical significance can be
obtained with smaller departure from the hypothesized value
• Disadvantage is that once committed they cannot claim the departure
as significant when there is significant departure in opposite direction

35. Step 2:
• Decide on appropriate Test Statistic for the
Hypothesis: Such as critical ratio,.
– Each test statistic has a probability distribution. In this case
it is based on ‘standard normal distribution’ bcz sample
size is large (142) and pop. StDev is known (34.2)
Step 3:
• Select the level of significance for the Statistical Test
– When chosen before the statistical test is performed, is
called ‘alpha value’ denoted by . It gives the probability
of incorrectly rejecting the Null Hypothesis (should be
small, usually  = .05, .01, .001 )

36. – Another concept related to significance is P value
– P value : it is the probability of obtaining a result as
extreme as or more extrem than the one observed, if
Null Hypothesis is true (probability that the observed
result is due to chance alone)
– P value is always calculated after the statistical test
has been performed; if the value is less then , the
Null Hypothesis is rejected
Step 3:
• Determine the Value the Test Statistic must attain to be
declared Significant:
– The ‘Significant’ Value is called the critical value of the test
statistic

37. • Determining the critical value: each test
statistic has a distribution;
• The distribution of test statistic is divided into
an area of hypothesis acceptance and an area
of hypothesis rejection
• The area of acceptance and rejection are
determined by the value chosen for 

38. -1.96
+1.96
Acceptance area
Rejection Area
.025
+1.645
Acceptance area
Rejection Area
.05

39. Step 5 :
• Perform the calculations:
Z= X - / (/n)= 42.9-21.0/ (34.2/ 142)=
21.9/2.87 = 7.63
Step 6 :
Draw and state the conclusion!
When p value is very small as in above case,
authos report it as p<.001 or <.0001
The practice of reporting p value less than some
traditional value was established prior to
computer use!

40. Error of Hypothesis Testing
Power = 1-