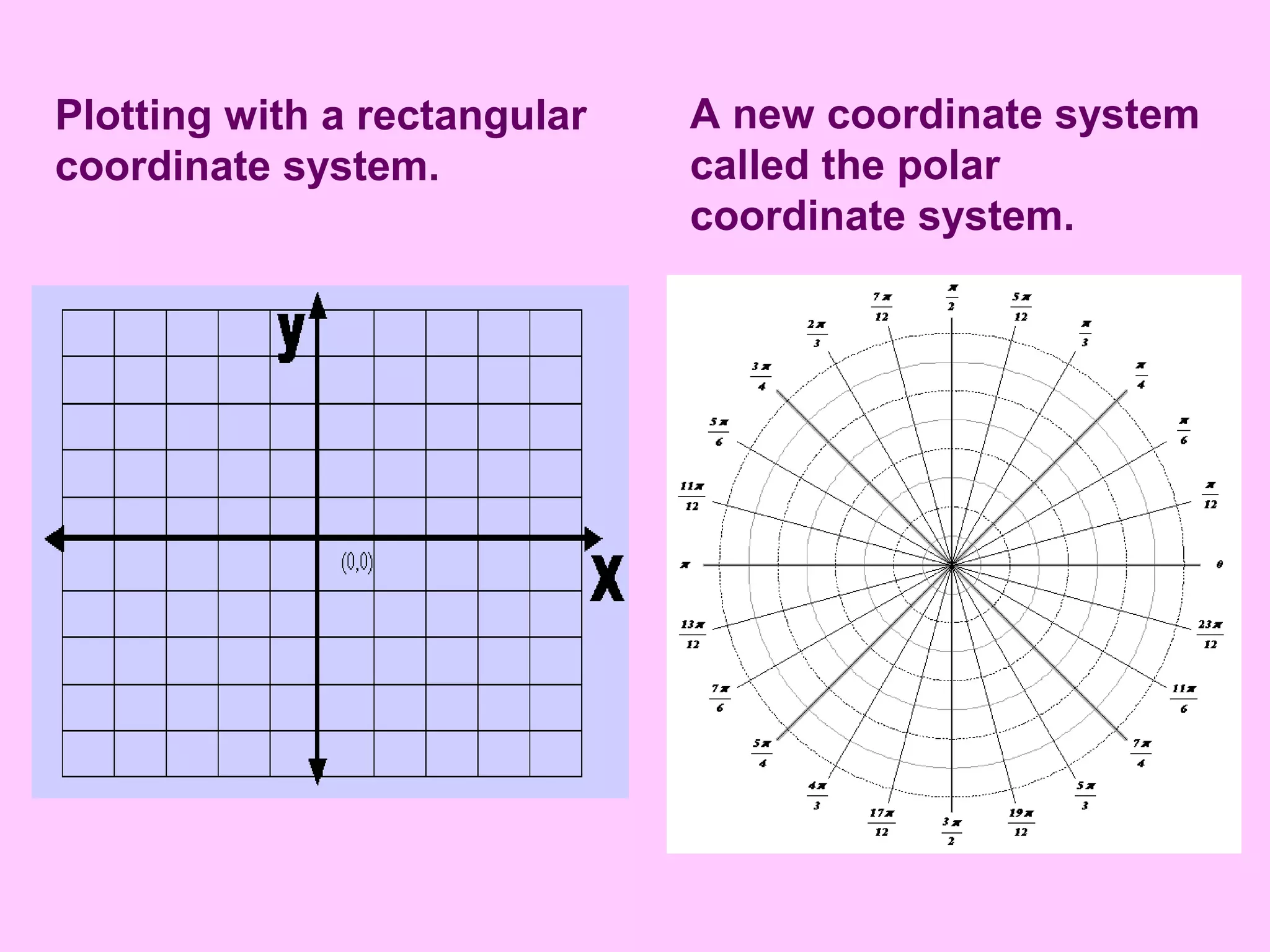
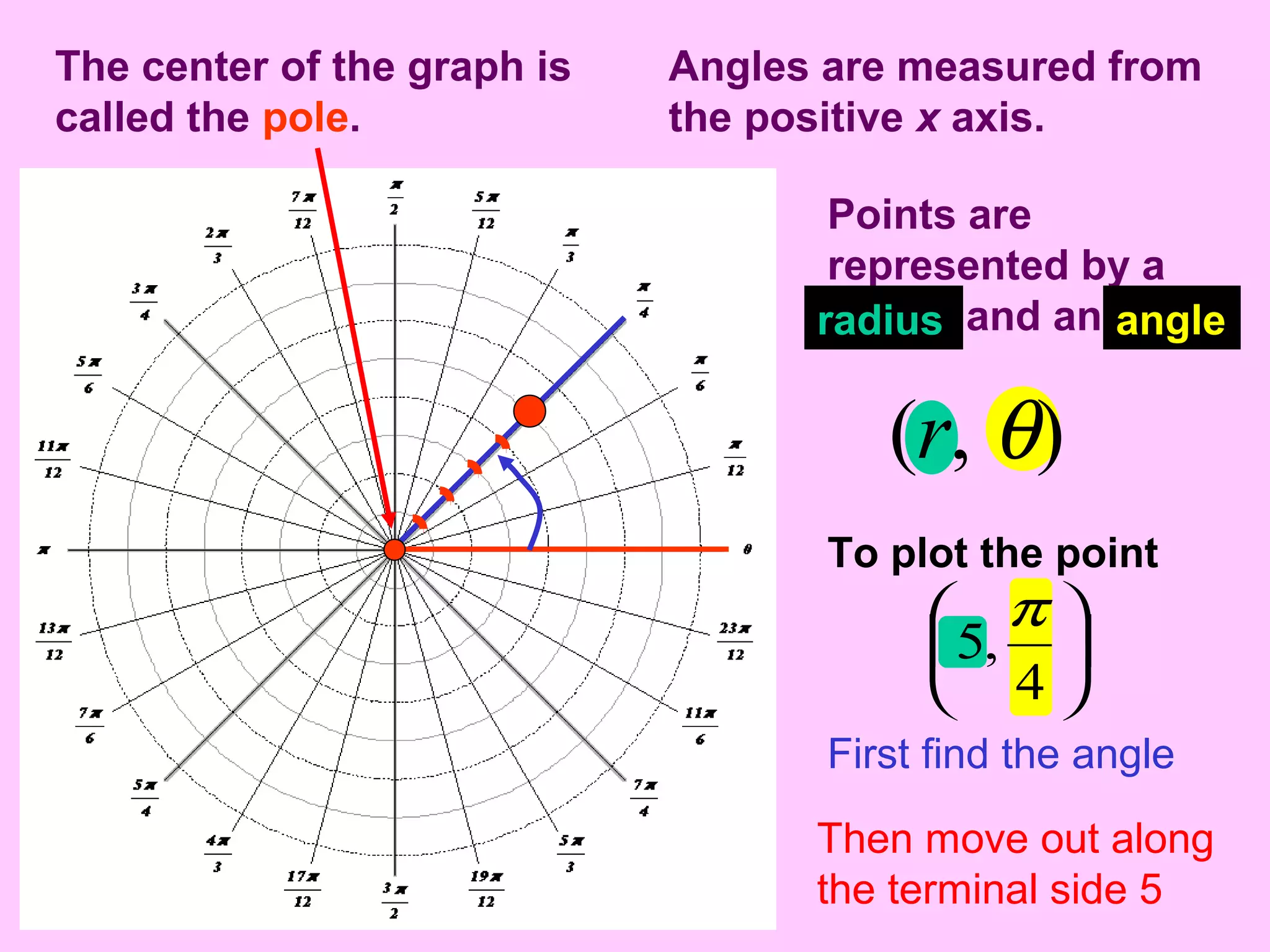
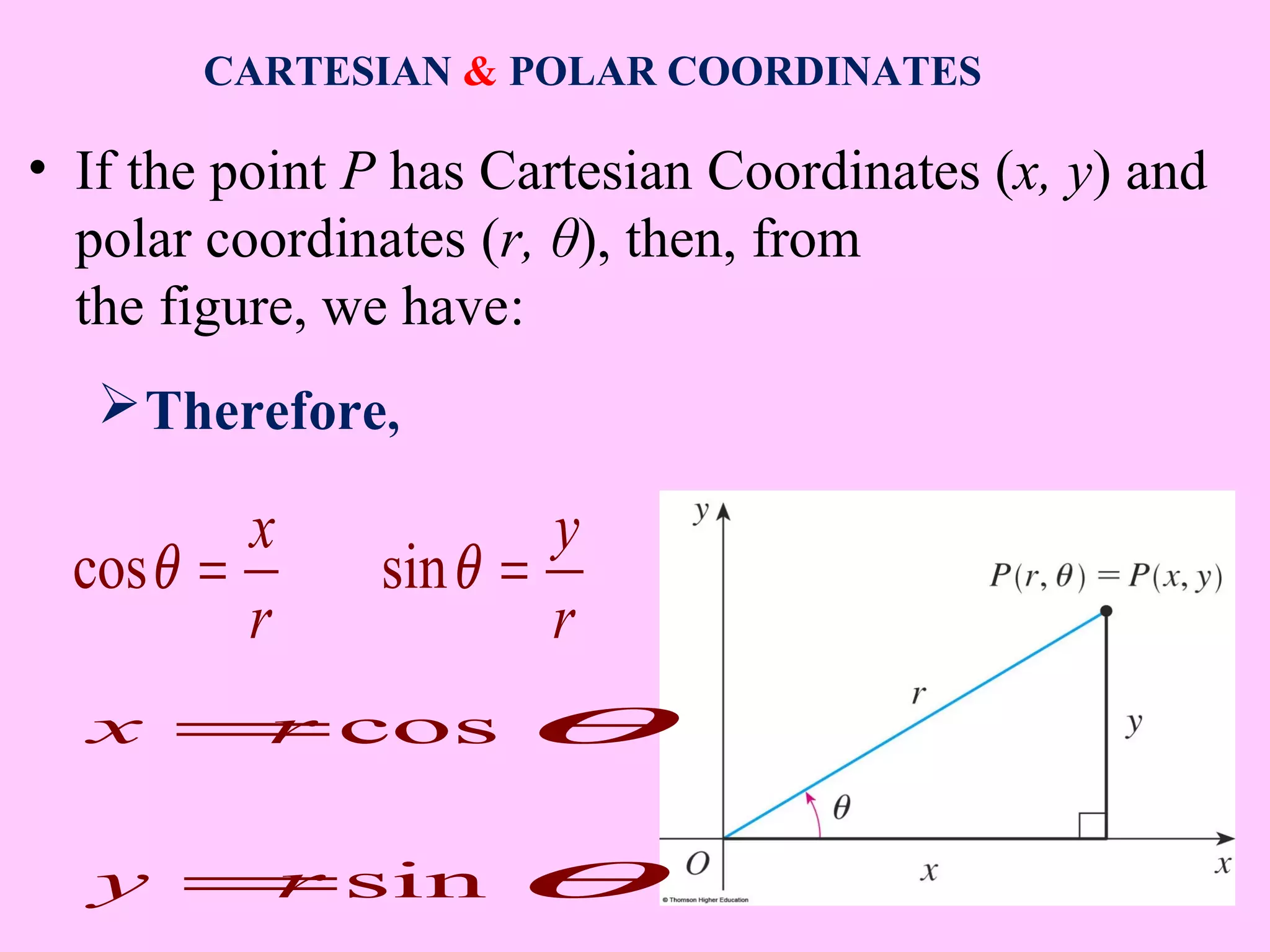
- The document introduces polar coordinates as an alternative coordinate system to Cartesian coordinates. - In polar coordinates, a point P is represented by an ordered pair (r, θ) where r is the distance from a fixed point called the pole (or origin) to P, and θ is the angle between the polar axis and the line from the pole to P. - Formulas are provided to convert between Cartesian (x, y) coordinates and polar (r, θ) coordinates. Specifically, r2 = x2 + y2 and θ = tan-1(y/x). 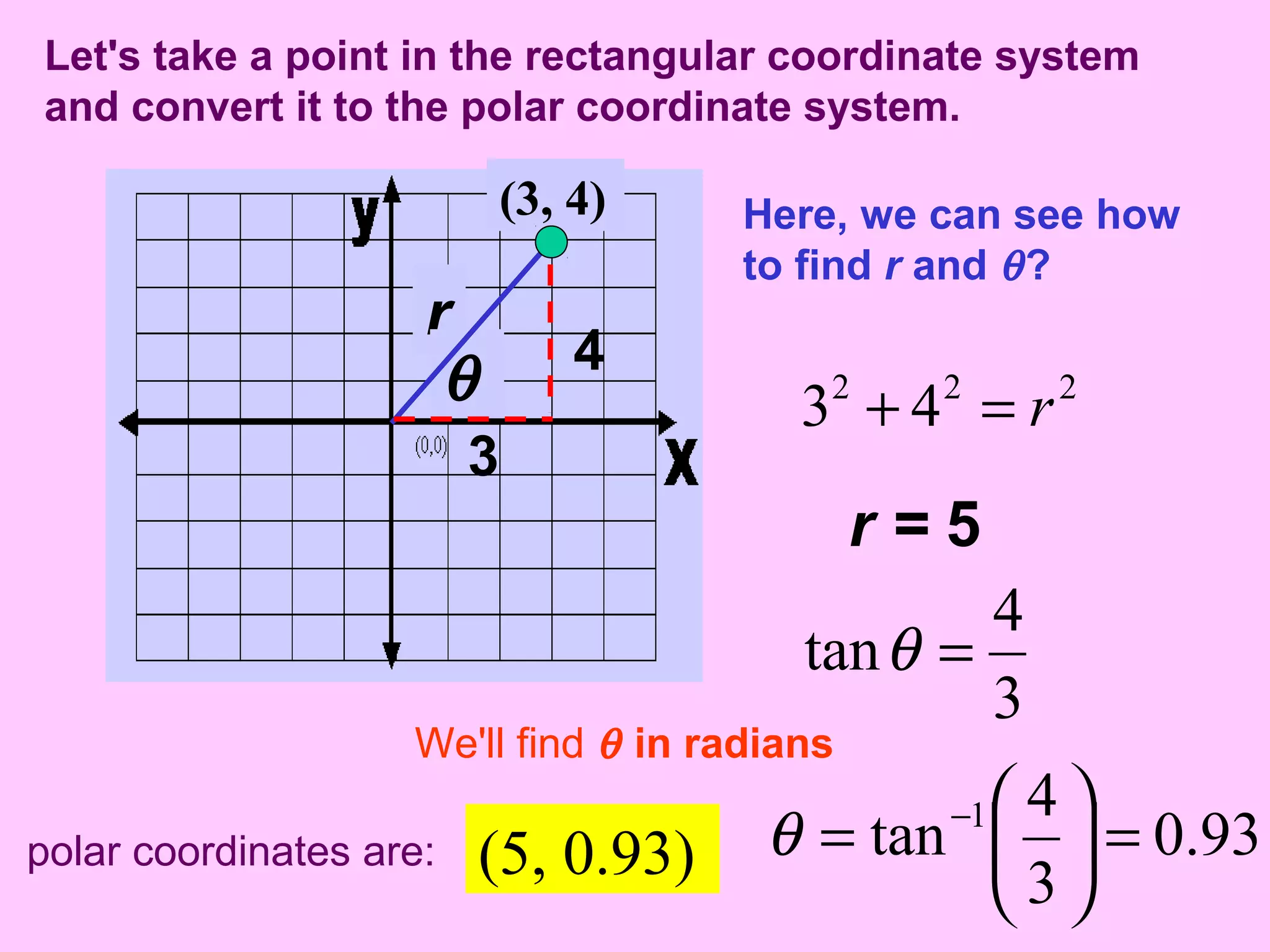- An example shows calculating the polar coordinates (5, 0.93) for the Cartesian point (3, 4).

2. Presented ByPresented By
Sonya Akter Rupa
ID-315161009
Department of CSE

3. Presented ToPresented To
Pro.Dr.Abu Zafor Ziauddin Ahamed
Lecturer of Physics
Hamdard University Bangladesh

4. (r, θ)

5. • A coordinate system represents a point in the
plane by an ordered pair of numbers called
coordinates.
• Usually, we use Cartesian coordinates, which are
directed distances from two perpendicular axes.
• A coordinate system introduced by Newton, called
the polar coordinate system.
Polar Co-ordinate system

6. • We choose a point in the plane that is called the pole (or
origin) and is labeled O.
• Then, we draw a ray (half-line) starting at O called the polar
axis.
• If P is any other point in the plane, let
 r be the distance from O to P.
 θ be the angle (usually measured in radians)
between the polar axis and the line OP.
Pole and Polar-axis

7. Plotting with a rectangular
coordinate system.
A new coordinate system
called the polar
coordinate system.

8. The center of the graph is
called the pole.
Angles are measured from
the positive x axis.
Points are
represented by a
radius and an angle
(r, θ)
radius angle
To plot the point






4
,5
π
First find the angle
Then move out along
the terminal side 5

9. CARTESIAN & POLAR COORDINATES
• If the point P has Cartesian Coordinates (x, y) and
polar coordinates (r, θ), then, from
the figure, we have:
cos sin
x y
r r
θ θ= =
Therefore,
cos
sin
x r
y r
θ
θ
=
=

10. Let's generalize this to find formulas for converting from
rectangular to polar coordinates.
(x, y)
r
θ y
x
222
ryx =+
x
y
=θtan
22
yxr +=






= −
x
y1
tanθ

11. Let's take a point in the rectangular coordinate system
and convert it to the polar coordinate system.
(3, 4)
r
θ
Here, we can see how
to find r and θ?
4
3
r = 5
222
43 r=+
3
4
tan =θ
93.0
3
4
tan 1
=





= −
θ
We'll find θ in radians
(5, 0.93)polar coordinates are:

12. Let's generalize the conversion from polar to rectangular
coordinates.
r
x
=θcos
( )θ,r
r
y
x
θ
r
y
=θsin
θcosrx =
θsinry =