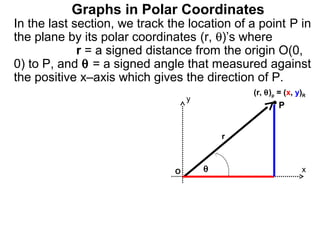
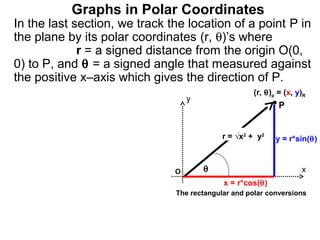
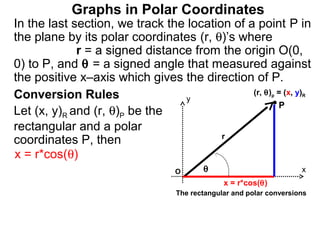
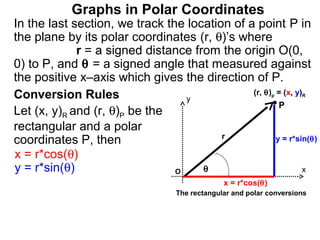
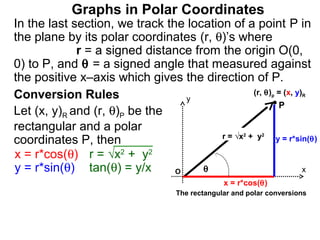
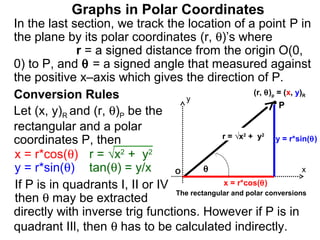
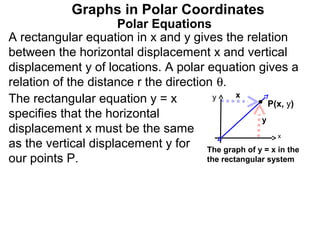
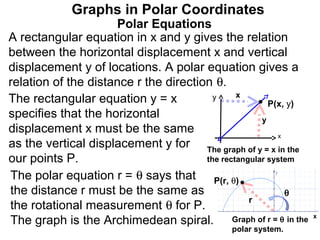
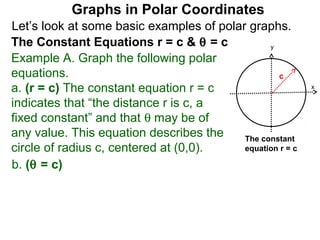
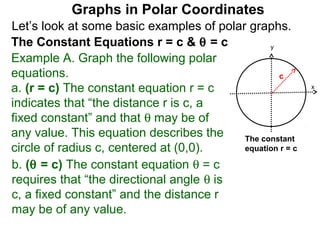
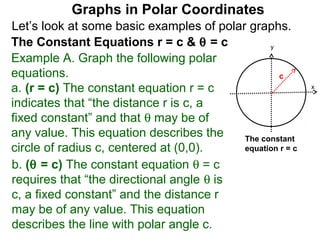
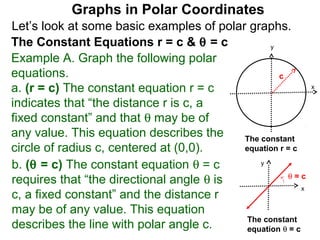
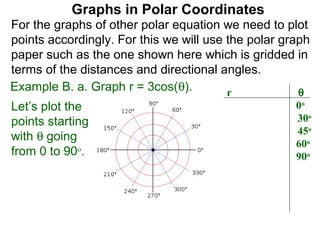
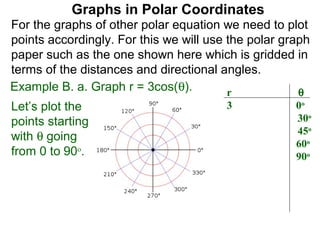
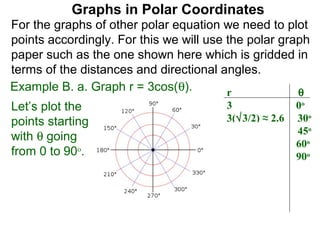
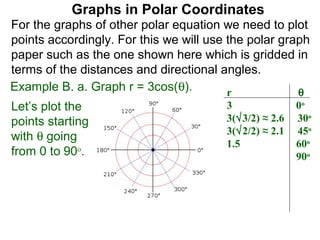
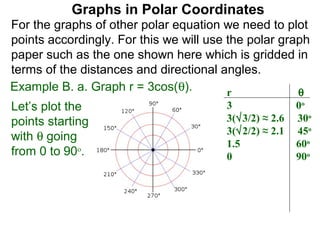
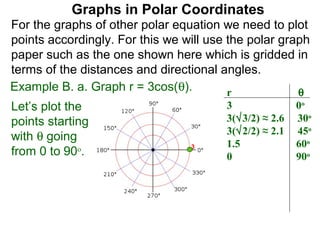
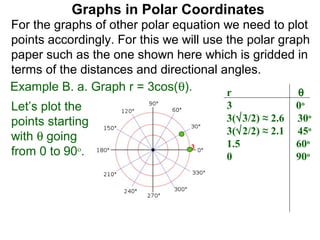
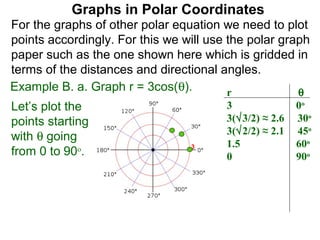
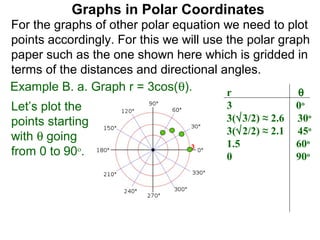
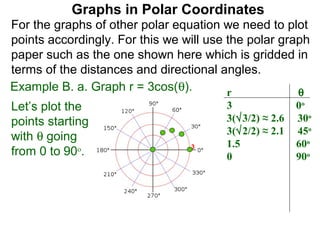
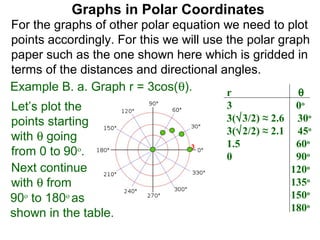
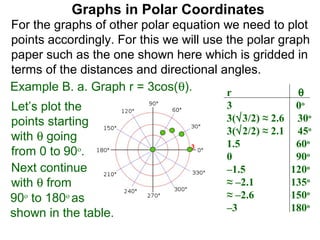
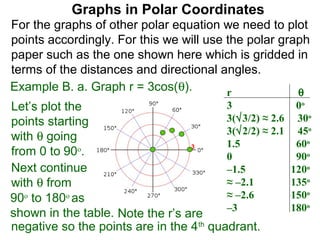
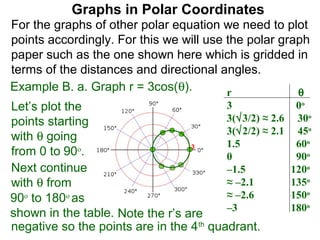
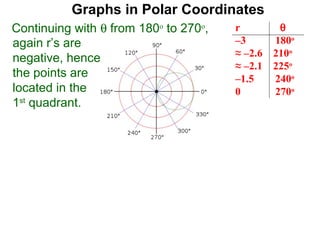
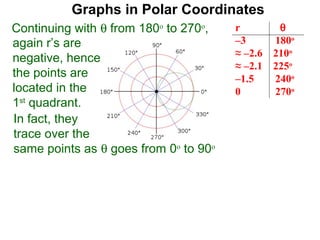
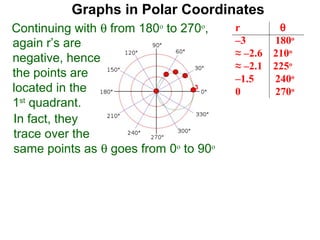
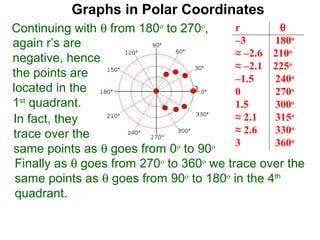
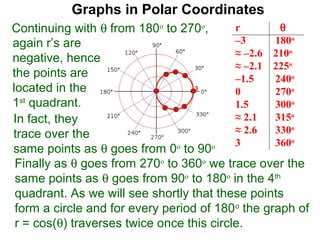
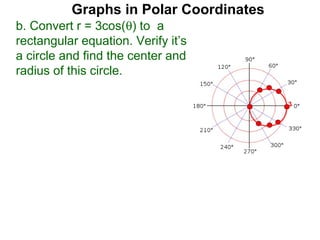
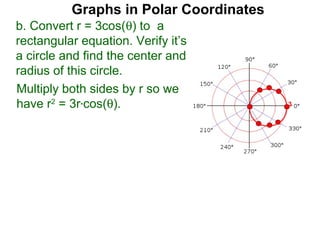
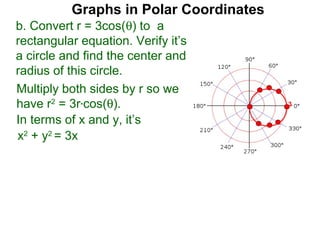
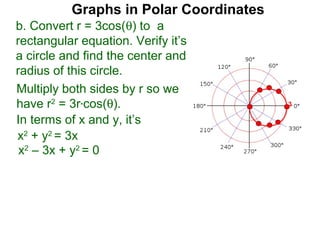
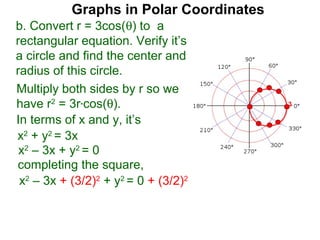
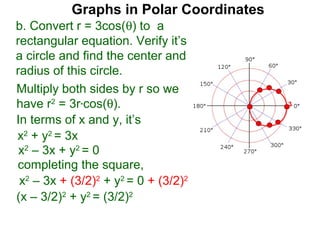
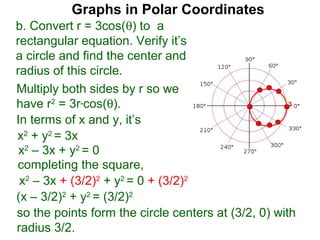
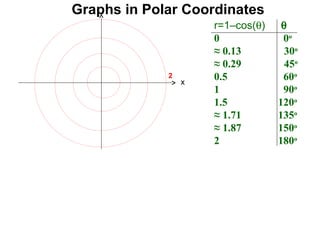
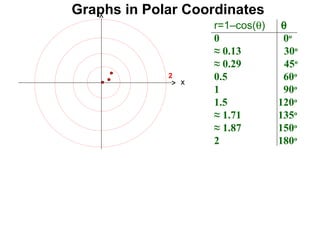
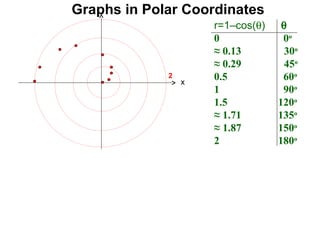
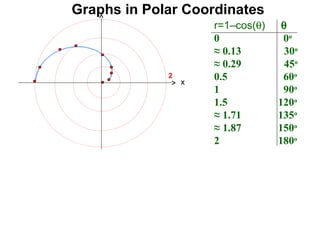
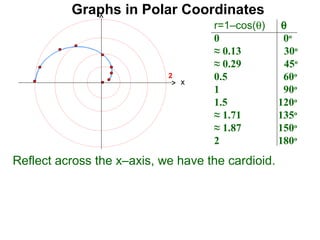
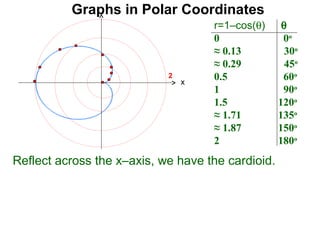
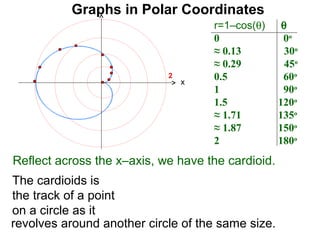
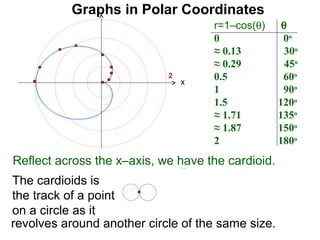
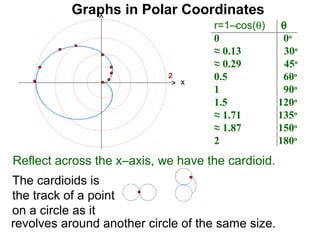
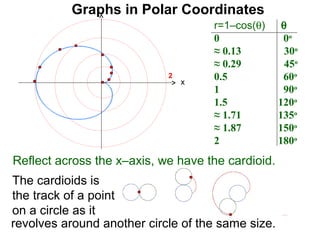
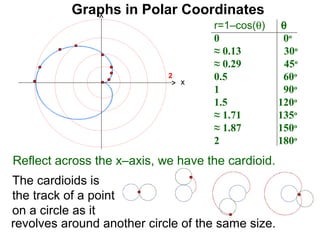
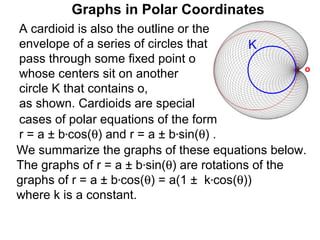
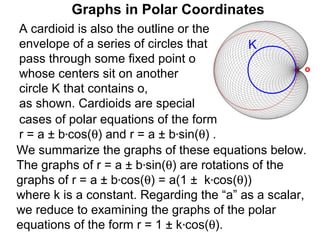
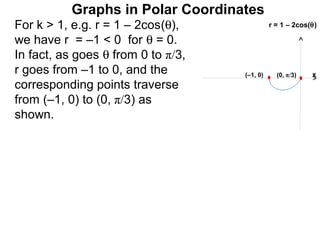
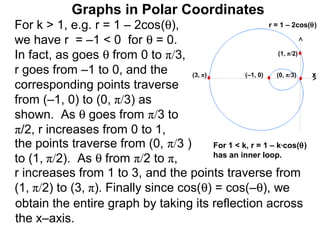
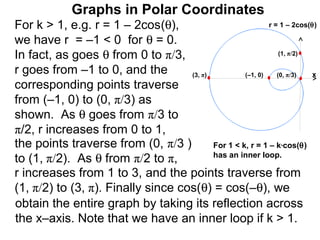
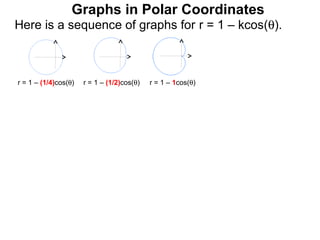
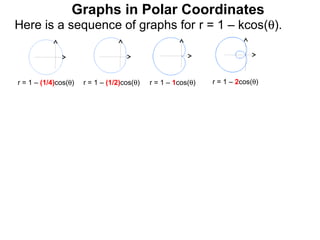
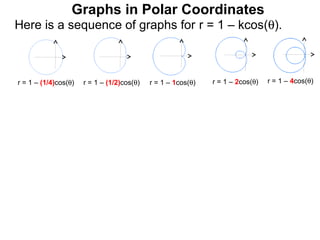
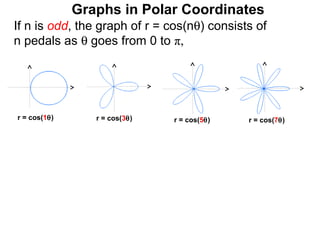
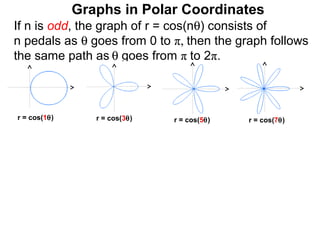
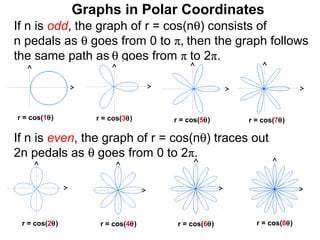
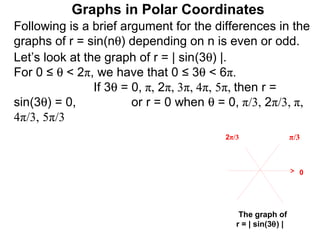
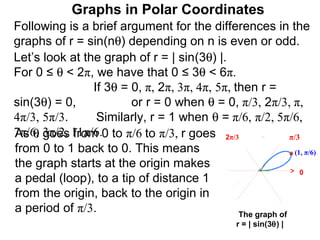
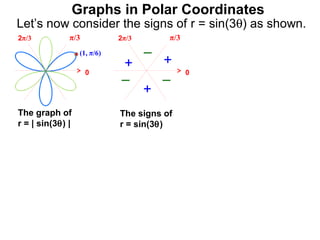
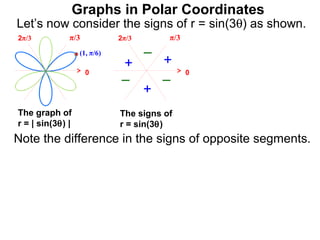
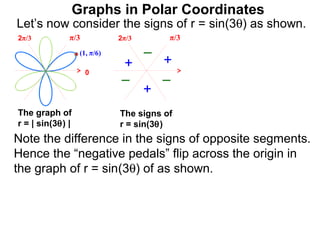
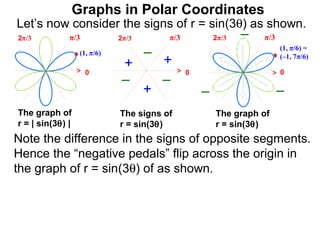
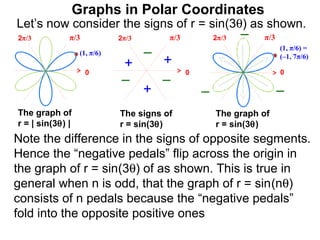
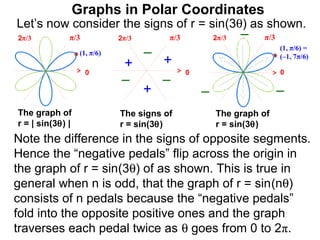
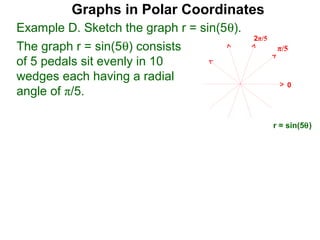
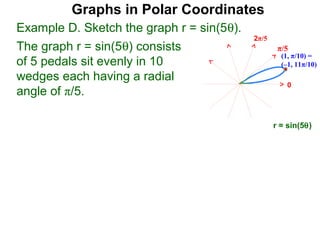
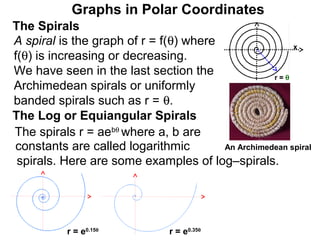
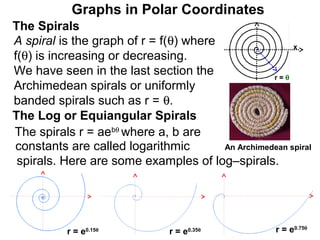
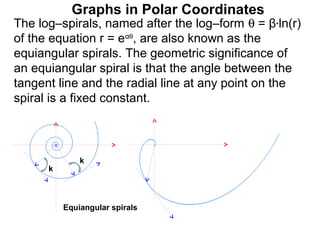
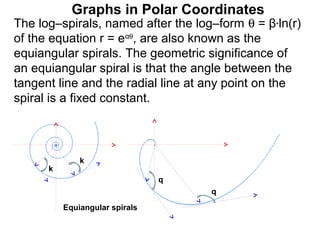
The document discusses graphs in polar coordinates. It begins by reviewing how polar coordinates (r, θ) represent a point P, where r is the distance from the origin and θ is the angle relative to the x-axis. It then discusses how to convert between rectangular (x, y) and polar (r, θ) coordinates. The document explains that polar equations relate r and θ, giving the example of r = θ which graphs as an Archimedean spiral. It also discusses the graphs of constant equations like r = c, which is a circle, and θ = c, which is a line. The document concludes by explaining how to graph other polar equations by plotting points.