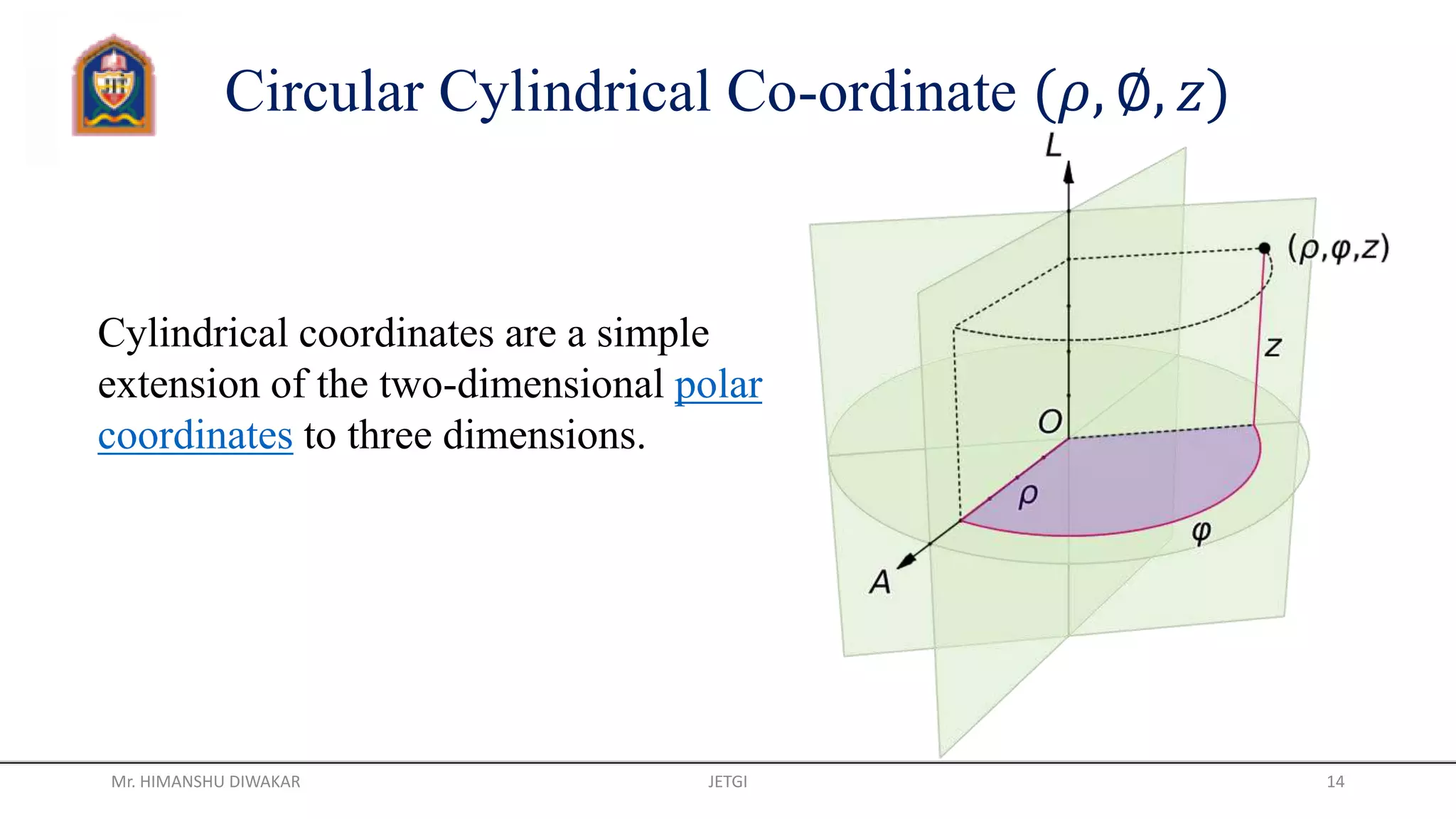
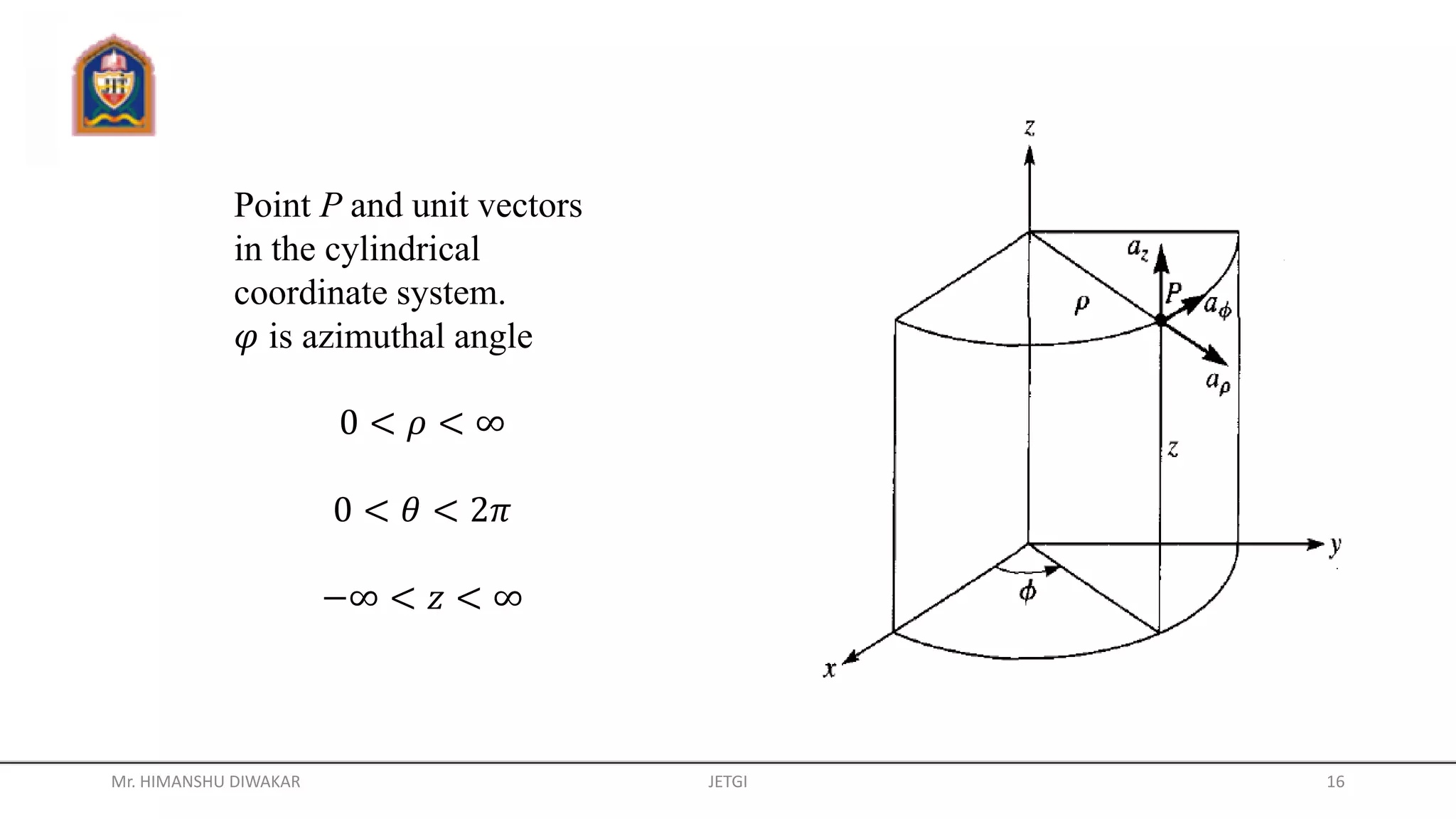
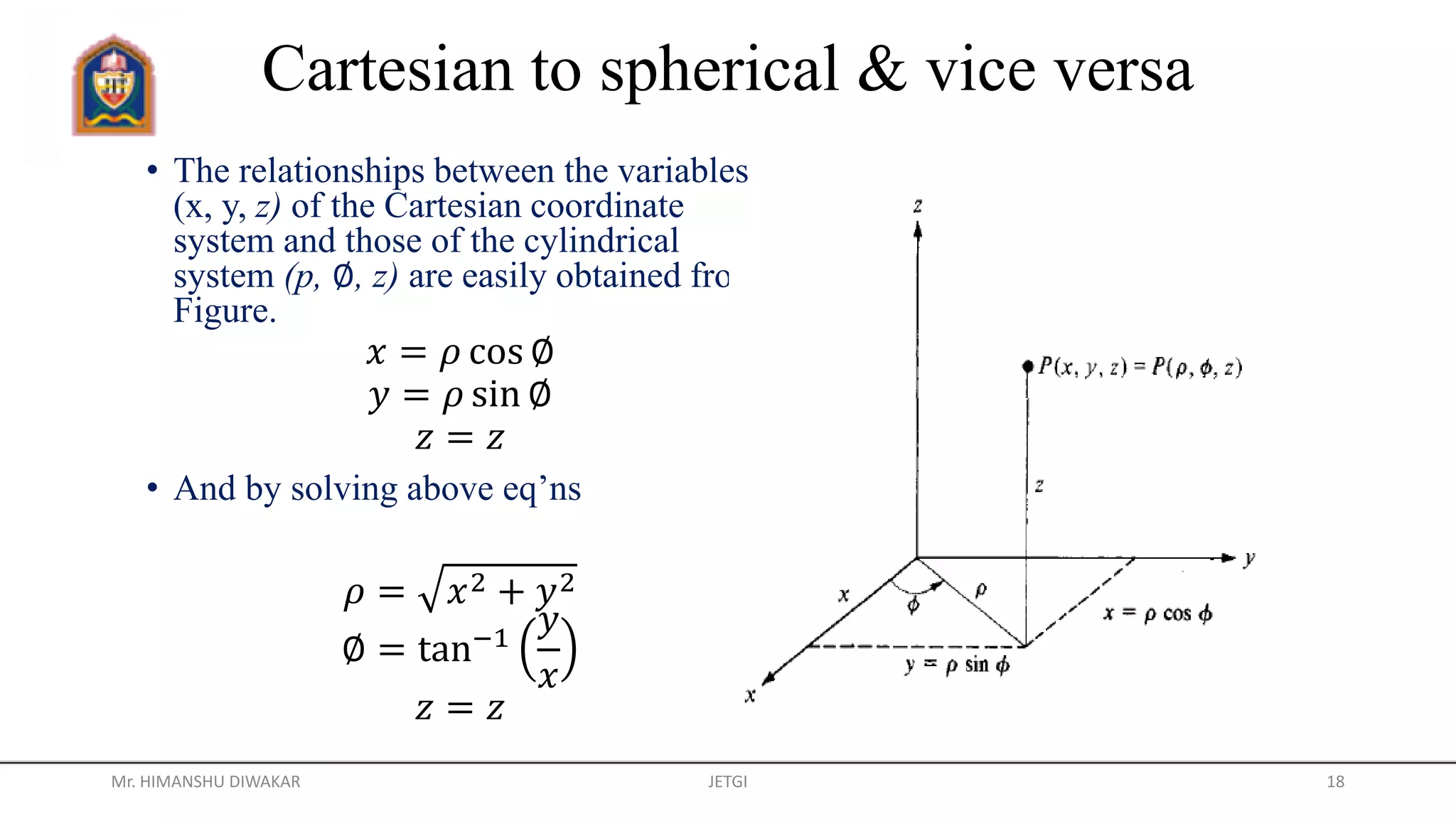
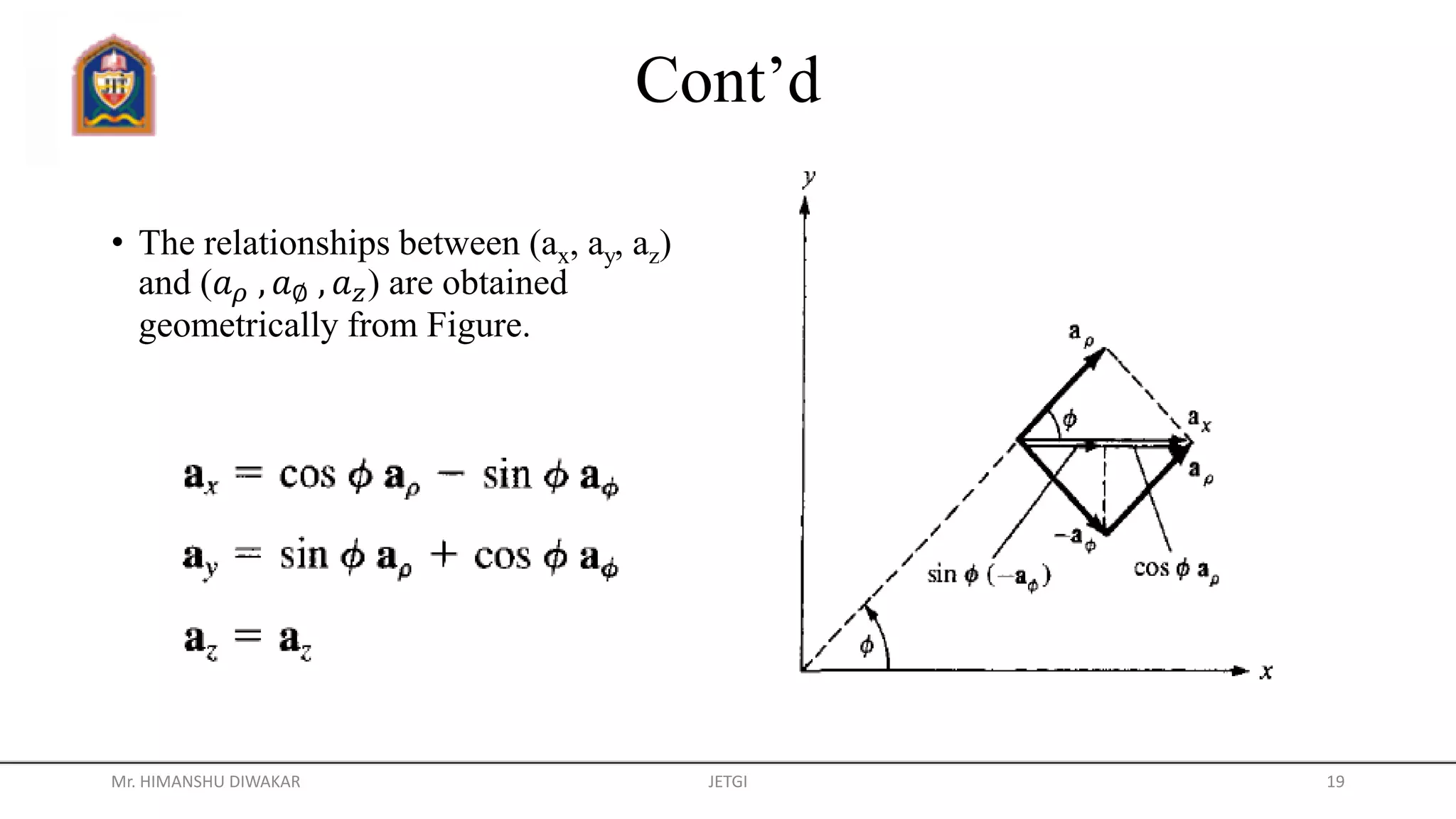
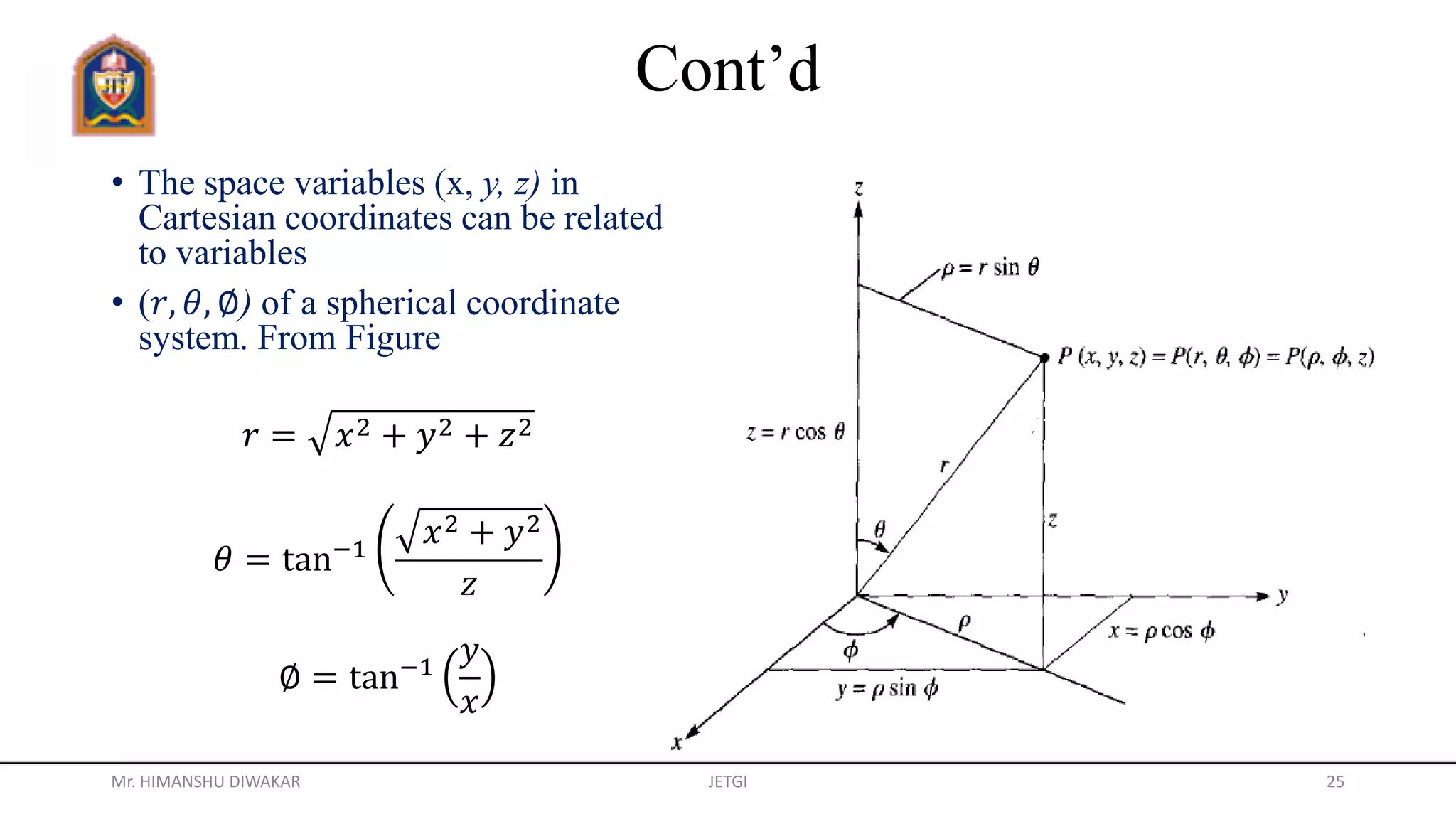
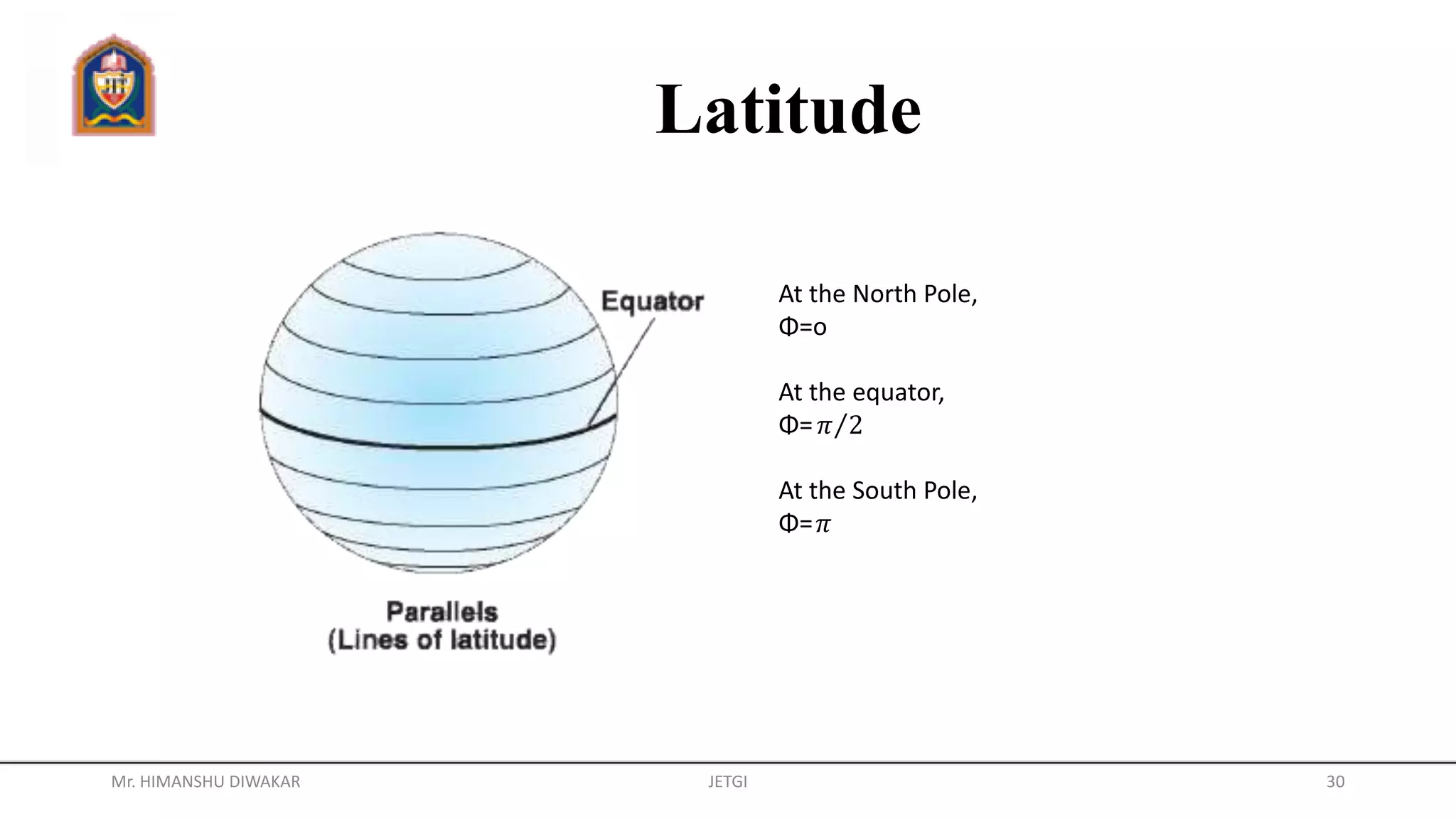
This document provides information about different coordinate systems including polar, cylindrical, Cartesian, and spherical coordinate systems. It describes key aspects of each system such as their components, definitions, relationships between variables in different systems, and applications. Real-world examples of how coordinate systems are used for map projections, global positioning systems, and air traffic control are also discussed.

1. Co-ordinate Geometry
Mr. HIMANSHU DWAKAR
Assistant professor
Department of ECE
JETGI
Mr. HIMANSHU DIWAKAR JETGI 1

2. Mr. HIMANSHU DIWAKAR JETGI 2

3. Mr. HIMANSHU DIWAKAR JETGI 3

4. GeneralDefinition
A co-ordinate system is a system designed to establish positions with
respect to given reference points.
The co-ordinate system consists of one or more reference points, the style
of measurement (linear or angular) from those reference points, and the
directions (or axes) in which those measurements will be taken.
Mr. HIMANSHU DIWAKAR JETGI 4

5. 1. POLAR CO-ORDINATE SYSTEM: It is
a two-dimensional coordinate system in
which each point on a plane in
determined by a distance from a fixed
point and an angle from a fixed direction.
(r,θ)
2. CYLINDRICAL CO-ORDINATE
SYSTEM: It is a three-dimensional
coordinate system, where each point is
specified by the two polar coordinates of
its perpendicular projection onto some
fixed plane, and by its distance from the
plane. (ρ,Ф,z)
Mr. HIMANSHU DIWAKAR JETGI 5

6. CLASSIFICATIONS
4. CARTESIAN CO-ORDINATE
SYSTEM: It specifies each point
uniquely in a plan by a pair of
numerical coordinates, which are
the signed distances from the point
to two fixed perpendicular directed
lines, measured in the same unit of
length.
3. SPHERICAL CO-ORDINATE SYSTEM: It is a
three-dimensional coordinate system, where
the position of a point is specified by three
numbers: the radial distance of that point
from a fixed origin, its elevation angle
measured from a fixed plane, and the
azimuth angle of its orthogonal projection on
that plane. (r,θ,Ф)
Mr. HIMANSHU DIWAKAR JETGI 6

7. Learning Co-ordinate geometry is not just to clear your present class but also
helps your understanding in various ways. Like–
1. Geometry is applicable in computers or cell phones.
2. The text file or PDF file which we open is itself an example of coordinate
plane.
3. In these, the words or images are written or modified with the use of
coordinate geometry.
4. Any PDF file, which contains text, images and different shapes, are placed
according to the 2-dimentional coordinate (x, y) system.
5. All the concepts like distances, slopes and simple trigonometry are also
applicable here.
USES OF CO-ORDINATE SYSTEM
Mr. HIMANSHU DIWAKAR JETGI 7

8. Describing position of any object
Coordinate system can be used to find the
position of any object from its original
place (called origin) to its present location
APPLICATIONS IN REAL LIFE
Location of Air Transport
We all have seen the aero-planes flying
in the sky but might have not thought of
how they actually reach the correct
destination. Actually all these air traffic
is managed and regulated by using
coordinate geometry.
Mr. HIMANSHU DIWAKAR JETGI 8

9. Map Projections
Map Projection is a technique to
map any 3D curved object on a
flat 2D surface.
APPLICATIONS IN REAL LIFE
The Global Positioning System (GPS):
GPS is a space based satellite navigation system
that provides location and time information in all
weather conditions. In a GPS, the longitude and
the latitude of a place are its coordinates. The
distance formula is used to find the distance
between 2 places in a GPS.
Mr. HIMANSHU DIWAKAR JETGI 9

10. In real life, when weather forecasters
are tracking hurricanes, they note the
absolute location on a periodic basis to
see the path of the storm and try to
predict the future path based partially
on these findings.
APPLICATIONS IN REAL LIFE
A latitude measurement indicates locations at a given
angle north or south of Earth’s equator. So, latitude
measurements range from 90° North at the North Pole
to 0° at the equator to 90° South at the South Pole.
A longitude measurement indicates locations at a
given angle east or west of an imaginary north-south
line called the prime meridian, which runs through
Greenwich, England. Longitude measurements begin
at 0° at the prime meridian and extend 180° both to
the west and to the east.
Mr. HIMANSHU DIWAKAR JETGI 10

11. Now imagine what if coordinate system doesn’t exist. Pilots, aircraft
controller, passengers in the flight, persons waiting for the flight all will not
be able to get the location or position of aircraft. These will also definitely
increase the chances of aircraft crushes. So from here we can easily say that
coordinate system is one of the most important parts of air transport.
WHAT WILL HAPPEN IF IT DOES NOT EXISTS?
Mr. HIMANSHU DIWAKAR JETGI 11

12. Circular Cylindrical Co-ordinate
System
Mr. HIMANSHU DIWAKAR JETGI 12

13. An overview
Cylindrical coordinate
surfaces. The three
orthogonal
components, ρ(green), φ(red),
and z (blue), each increasing
at a constant rate. The point is
at the intersection between
the three colored surfaces.
Mr. HIMANSHU DIWAKAR JETGI 13

14. Circular Cylindrical Co-ordinate (𝜌, ∅, 𝑧)
Cylindrical coordinates are a simple
extension of the two-dimensional polar
coordinates to three dimensions.
Mr. HIMANSHU DIWAKAR JETGI 14

15. Definition
The three coordinates (ρ, φ, z) of a point P are defined as:
• The radial distance ρ is the Euclidean distance from the z-axis to the
point P.
• The azimuth φ is the angle between the reference direction on the
chosen plane and the line from the origin to the projection of P on
the plane.
• The height z is the signed distance from the chosen plane to the
point P
Mr. HIMANSHU DIWAKAR JETGI 15

16. Point P and unit vectors
in the cylindrical
coordinate system.
𝜑 is azimuthal angle
0 < 𝜌 < ∞
0 < 𝜃 < 2𝜋
−∞ < 𝑧 < ∞
Mr. HIMANSHU DIWAKAR JETGI 16

17. • A vector A in cylindrical coordinates can be written as
𝐴 𝜌, 𝐴∅, 𝐴 𝑍
𝐴 = 𝐴 𝜌 𝑎 𝜌 + 𝐴∅ 𝑎∅ + 𝐴 𝑧 𝑎 𝑧
𝐴 = 𝐴 𝜌
2
+ 𝐴 𝜌
2
+ 𝐴 𝜌
2
Mr. HIMANSHU DIWAKAR JETGI 17

18. Cartesian to spherical & vice versa
• The relationships between the variables
(x, y, z) of the Cartesian coordinate
system and those of the cylindrical
system (p, ∅, z) are easily obtained from
Figure.
𝑥 = 𝜌 cos ∅
𝑦 = 𝜌 sin ∅
𝑧 = 𝑧
• And by solving above eq’ns
𝜌 = 𝑥2 + 𝑦2
∅ = tan−1
𝑦
𝑥
𝑧 = 𝑧
Mr. HIMANSHU DIWAKAR JETGI 18

19. Cont’d
• The relationships between (ax, ay, az)
and (𝑎 𝜌 , 𝑎∅ , 𝑎 𝑧) are obtained
geometrically from Figure.
Mr. HIMANSHU DIWAKAR JETGI 19

20. Cont’d
Mr. HIMANSHU DIWAKAR JETGI 20

21. SPHERICAL CO-ORDINATE
SYSTEM
Mr. HIMANSHU DIWAKAR JETGI 21

22. Introduction to Spherical Co-ordinate System
• Spherical coordinates are a system of curvilinear coordinates that
are natural for describing positions on a sphere or spheroid.
The coordinate ρ is the distance from P to the
origin.
θ is the angle between the positive x-axis and the
line segment from the origin to Q.
ϕ is the angle between the positive z-axis and the
line segment from the origin to P.
Mr. HIMANSHU DIWAKAR JETGI 22

23. Location of a Point
• The spherical coordinate system extends polar coordinates into 3D
by using an angle ϕ for the third coordinate. This gives
coordinates (r,θ,ϕ) consisting of
Co-ordinate Name Range Definition
r radius 0≤r<∞ distance from the origin
θ azimuth −π<θ≤π
angle from the x-axis in the x–
y plane
ϕ elevation −π/2<ϕ≤π/2 angle up from the x–y plane
The location of any point in spherical is (r,θ,ϕ)
Mr. HIMANSHU DIWAKAR JETGI 23

24. Relationship b/w Spherical and Cartesian coordinate
System
x = ρ sinϕ cosθ
y = ρ sin ϕsinθ
z = ρ cosϕ.
Mr. HIMANSHU DIWAKAR JETGI 24

25. Cont’d
• The space variables (x, y, z) in
Cartesian coordinates can be related
to variables
• (𝑟, 𝜃, ∅) of a spherical coordinate
system. From Figure
𝑟 = 𝑥2 + 𝑦2 + 𝑧2
𝜃 = tan−1
𝑥2 + 𝑦2
𝑧
∅ = tan−1
𝑦
𝑥
Mr. HIMANSHU DIWAKAR JETGI 25

26. The unit vectors ax, ay, az and ar, 𝑎 𝜃, 𝑎∅ are
related as follows
Mr. HIMANSHU DIWAKAR JETGI 26

27. SPHEROIDS AND SPHERES
• The shape and size of a geographic coordinate system’s surface is
defined by a sphere or spheroid
The assumption
that the earth is a sphere is
possible for small-scale
maps (smaller than
1:5,000,000)
To maintain accuracy
for larger-scale maps (scales
of 1:1,000,000 or larger),
a spheroid is necessary to
represent the shape of the
Earth
A sphere is based on a circle, while a spheroid
(or ellipsoid) is based on an ellipse
Mr. HIMANSHU DIWAKAR JETGI 27

28. Latitude & Longitude
• A Geographic Coordinate System (GCS) uses a 3D spherical surface to define
locations on the Earth
• GCS uses the azimuth and elevation of the spherical coordinate system
• A point is referenced by its longitude and latitude values
• Longitude and latitude are angles measured from the earth’s center to a point
on the Earth’s surface.
Mr. HIMANSHU DIWAKAR JETGI 28

29. Latitude
• Horizontal line
• It is the angular distance, in degrees, minutes, and seconds of a
point north or south of the Equator.
• Often referred to as parallels.
• The coordinate ϕ corresponds to latitude
• On the Earth, latitude is measured as angular distance from the
equator.
• In spherical coordinates, latitude is measured as the angular
distance from the North Pole
Mr. HIMANSHU DIWAKAR JETGI 29

30. At the North Pole,
Φ=o
At the equator,
Φ=
At the South Pole,
Φ=
𝜋 2
𝜋
Latitude
Mr. HIMANSHU DIWAKAR JETGI 30

31. Longitude
• Vertical line
• It is the angular distance in degrees, minutes and seconds of a point,
East or West of the Prime (Greenwich) Meridian
• Often referred to as Meridians
• Each longitude line measures 12,429.9 miles
• The coordinate θ corresponds to longitude
• θ is a measurement of angular distance from the horizontal axis.
Mr. HIMANSHU DIWAKAR JETGI 31

32. Longitude
At the North pole
Θ=
At the equator
Θ=0 or 𝜋
At the south pole
Θ= -
𝜋 2
𝜋 2
Mr. HIMANSHU DIWAKAR JETGI 32

33. Latitude & Longitude
Distance between Lines
If we divide the circumference of the earth (approximately 25,000 miles) by 360
degrees, the distance on the earth's surface for each one degree of latitude
orlongitude is just over 69 miles, or 111 km.
Mr. HIMANSHU DIWAKAR JETGI 33

34. GPS (Global Positioning System)
• Space-based satellite navigation system
• Developed in 1973 to overcome the limitations of previous navigation systems
• Provides location and time information in all weather conditions, anywhere on
or near the Earth
Mr. HIMANSHU DIWAKAR JETGI 34

35. GPS
• Any desired location can be found by entering its coordinates in our GPS
device.
• We only need to know the latitude and longitude of that location to know
exactly where it is.
• Today GPS is a network on 30 satellites
Mr. HIMANSHU DIWAKAR JETGI 35

36. THANK YOU
Mr. HIMANSHU DIWAKAR JETGI 36