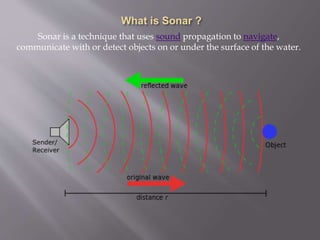
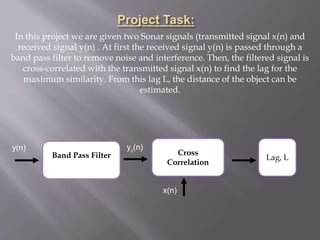
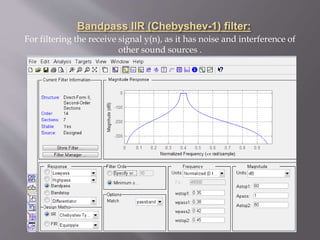
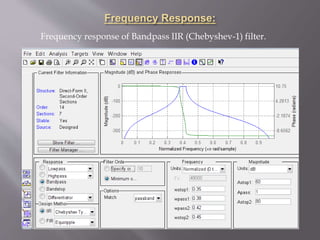
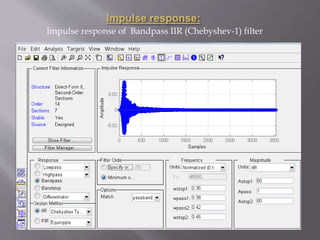
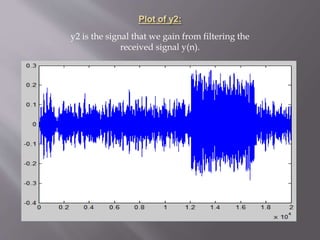
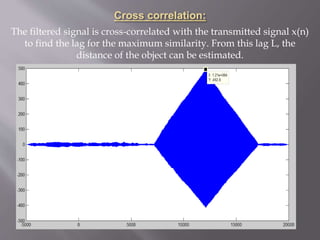
This project involves using sonar signals to estimate the distance of an object. The received sonar signal y(n) is passed through a bandpass filter to remove noise, producing the filtered signal y2(n). y2(n) is then cross-correlated with the transmitted signal x(n) to determine the lag L. Using the lag L, sampling frequency, and speed of sound in water, the distance to the object is estimated as 896.0050 meters.

1. DSP Project
Project Done By
Istiak Mahmood Ayon
ID: 021101005
Shahrin Ahammad Shetu
ID: 021101027

2. Sonar is a technique that uses sound propagation to navigate,
communicate with or detect objects on or under the surface of the water.

3.  Sonar uses a sound transmitter and a receiver.
Sonar creates a pulse of sound, and then listens
for the reflections (echo) of the pulse. To
measure the distance to an object, the time
from transmission of a pulse to reception is
measured and converted into a range (distance)
by knowing the speed of sound.

4. In this project we are given two Sonar signals (transmitted signal x(n) and
received signal y(n) . At first the received signal y(n) is passed through a
band pass filter to remove noise and interference. Then, the filtered signal is
cross-correlated with the transmitted signal x(n) to find the lag for the
maximum similarity. From this lag L, the distance of the object can be
estimated.
x(n)
y(n) y2(n)
Band Pass Filter Cross
Correlation
Lag, L

5. Transmitted signal x(n)

6. The Fast Fourier of the transmitted signal x(n).

7. 1) Magnitude response (dB)
2) Phase response (degree)

8. Received signal y(n).

9. 1) Magnitude response (dB)
2) Phase response (degree)

10. The Fast Fourier of the received signal y(n).

11. For filtering the receive signal y(n), as it has noise and interference of
other sound sources .

12. Frequency response of Bandpass IIR (Chebyshev-1) filter.

13. Impulse response:
Impulse response of Bandpass IIR (Chebyshev-1) filter

14. y2 is the signal that we gain from filtering the
received signal y(n).

15. The Fast Fourier of the received signal y2.

16. 1) Magnitude response (dB)
2) Phase response (degree)

17. The filtered signal is cross-correlated with the transmitted signal x(n)
to find the lag for the maximum similarity. From this lag L, the
distance of the object can be estimated.

18. Here
r=distance of the object.
t=time between the transmission and reception.
v=velocity of sound (in water).
L=Lag
Distance, r = v*t/2
Given
Sampling frequency Fs = 10KHz
Velocity of sound in water is v = 1,481m/s.
The time between transmission and reception can be
calculated from the lag L (t=L/Fs).

19. Code for distance measurement:
L=1.21*10^4;
Fs=10^4;
t=L/Fs;
v=1481;
r=(v*t)/2
Ans:
The distance ‘r’ is :-
r =
896.0050

20.  clc;
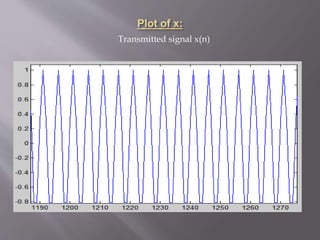
 plot(x) %Plot of transmitted signal x(n)
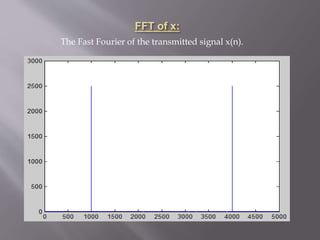
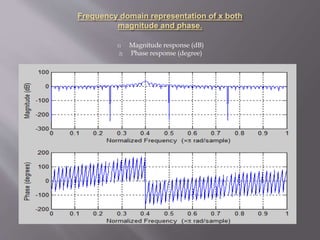
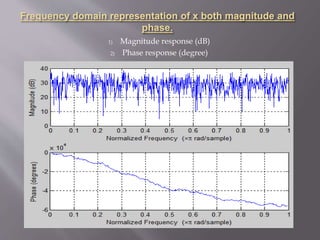
 figure,freqz(x) %Frequency response of x(n)
 X=fft(x);
 figure,plot(abs(X))
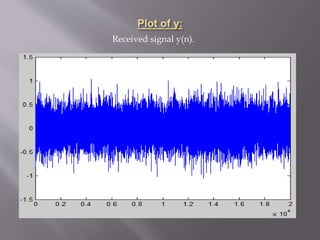
 figure,plot(y) %Plot of received signal y(n)
 figure,freqz(y) %Frequency response of y(n)
 Y=fft(y);
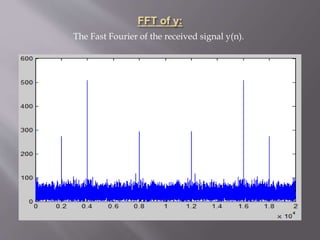
 figure,plot(abs(Y))
 [b,a]=SOS2tf(SOS,G);
 y2=filter(b,a,y); %filter calling.
 figure,plot(y2) % plot of filtered signal y2(n)
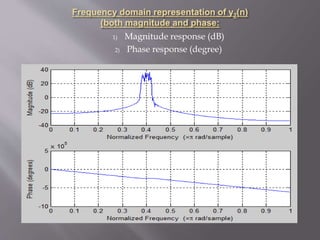
 figure,freqz(y2) %Frequency response of y(n)
 Y2=fft(y2);
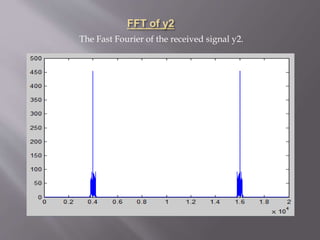
 figure,plot(abs(Y2))
 n0=1:length(x); % cross co-relation of transmitted
 n2=1:length(y2); % signal x(n) and filtered signal y2(n)
 [x1,n1]=sigfold(x,n0);
 [z,n]=conv_m(x1,n1,y2,n2);
 figure,plot(n,z)