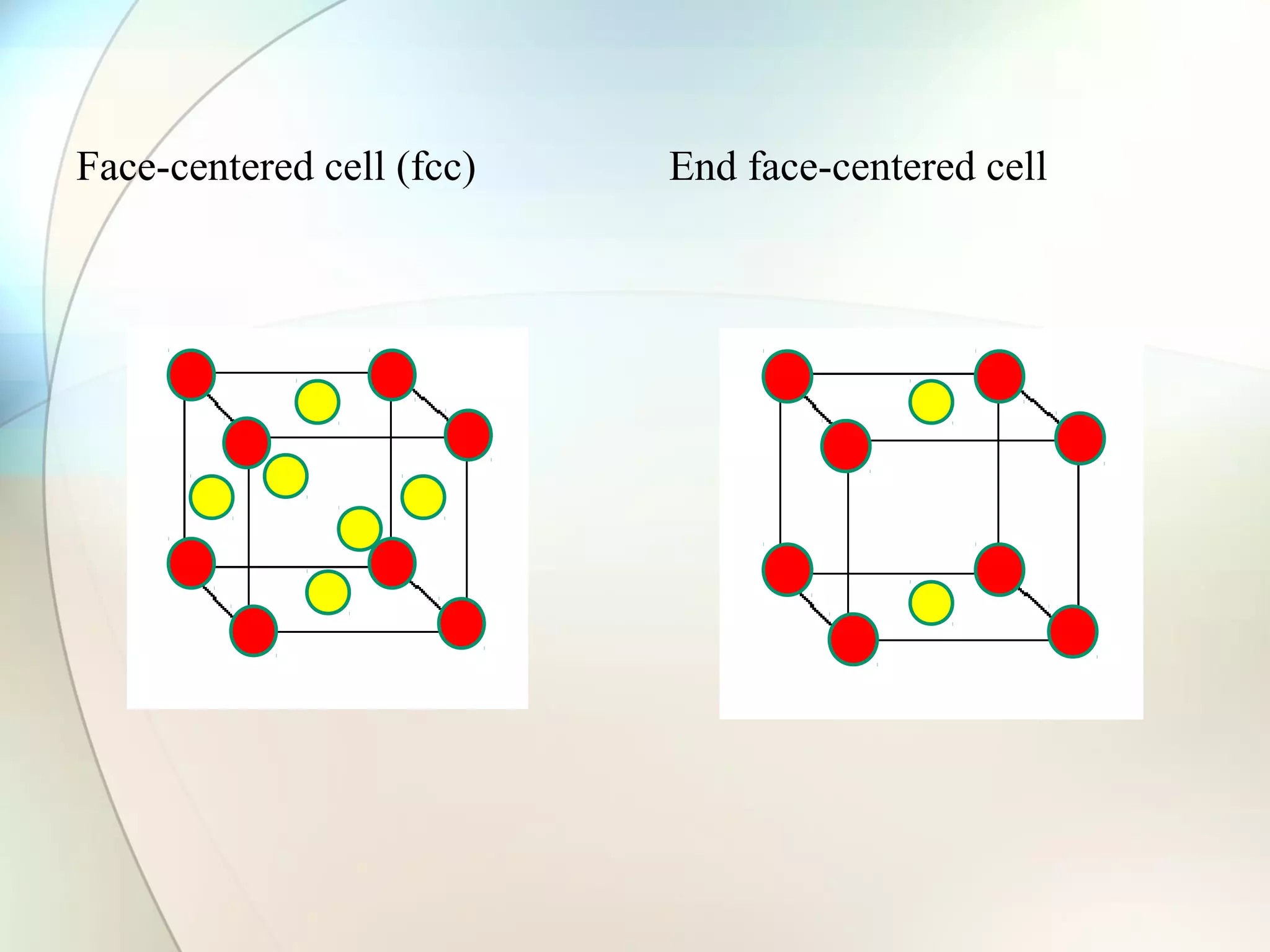
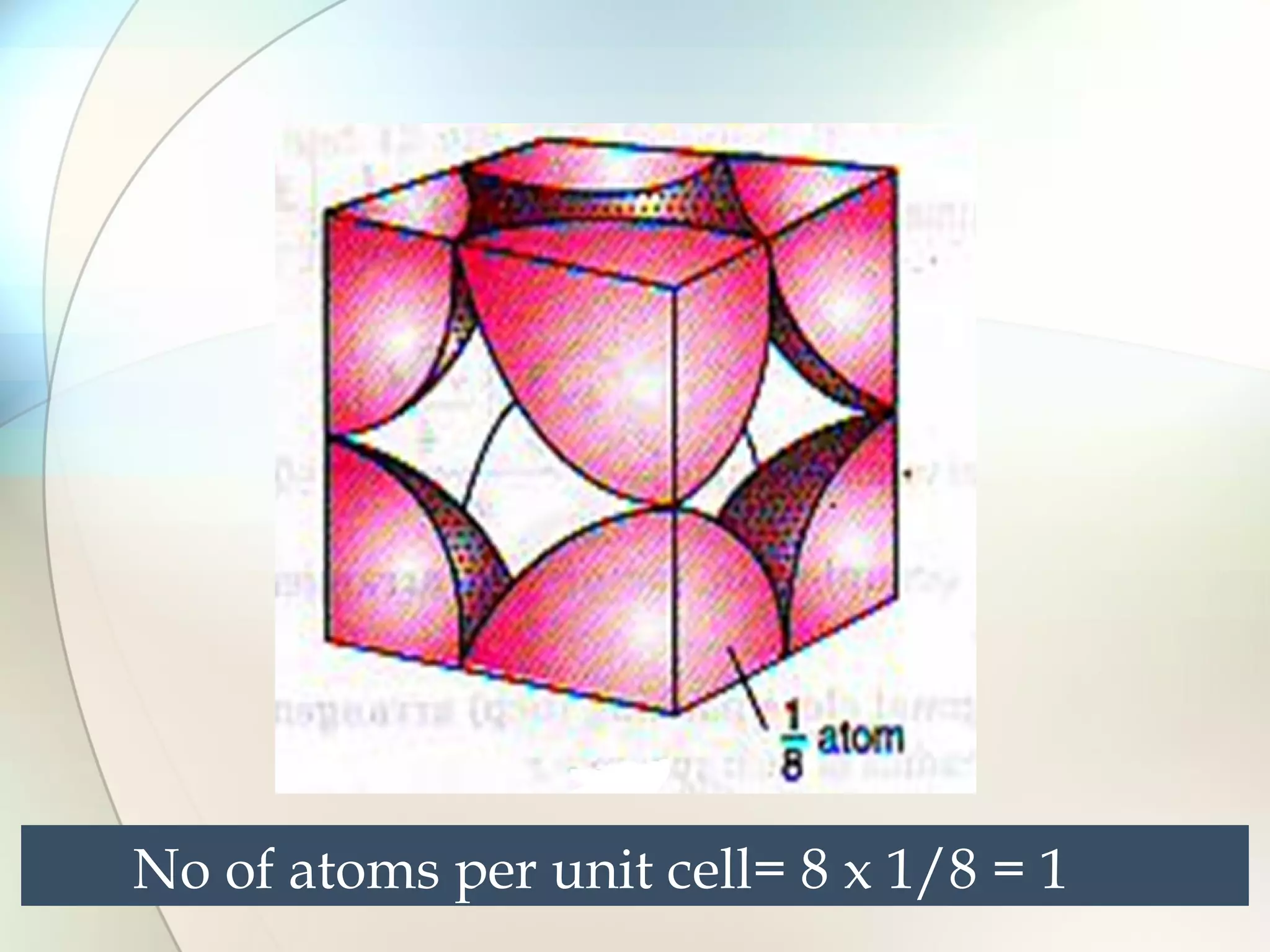
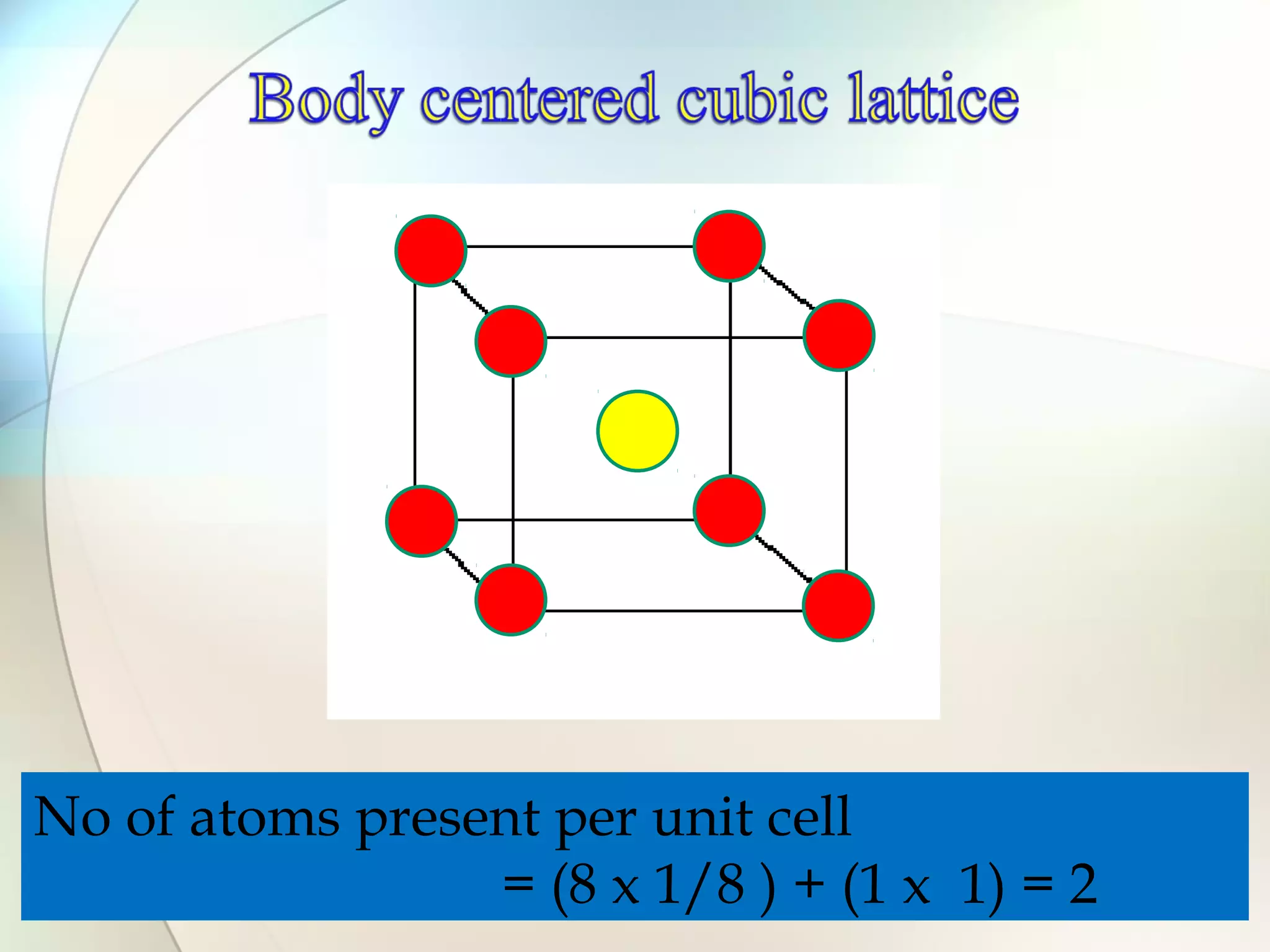
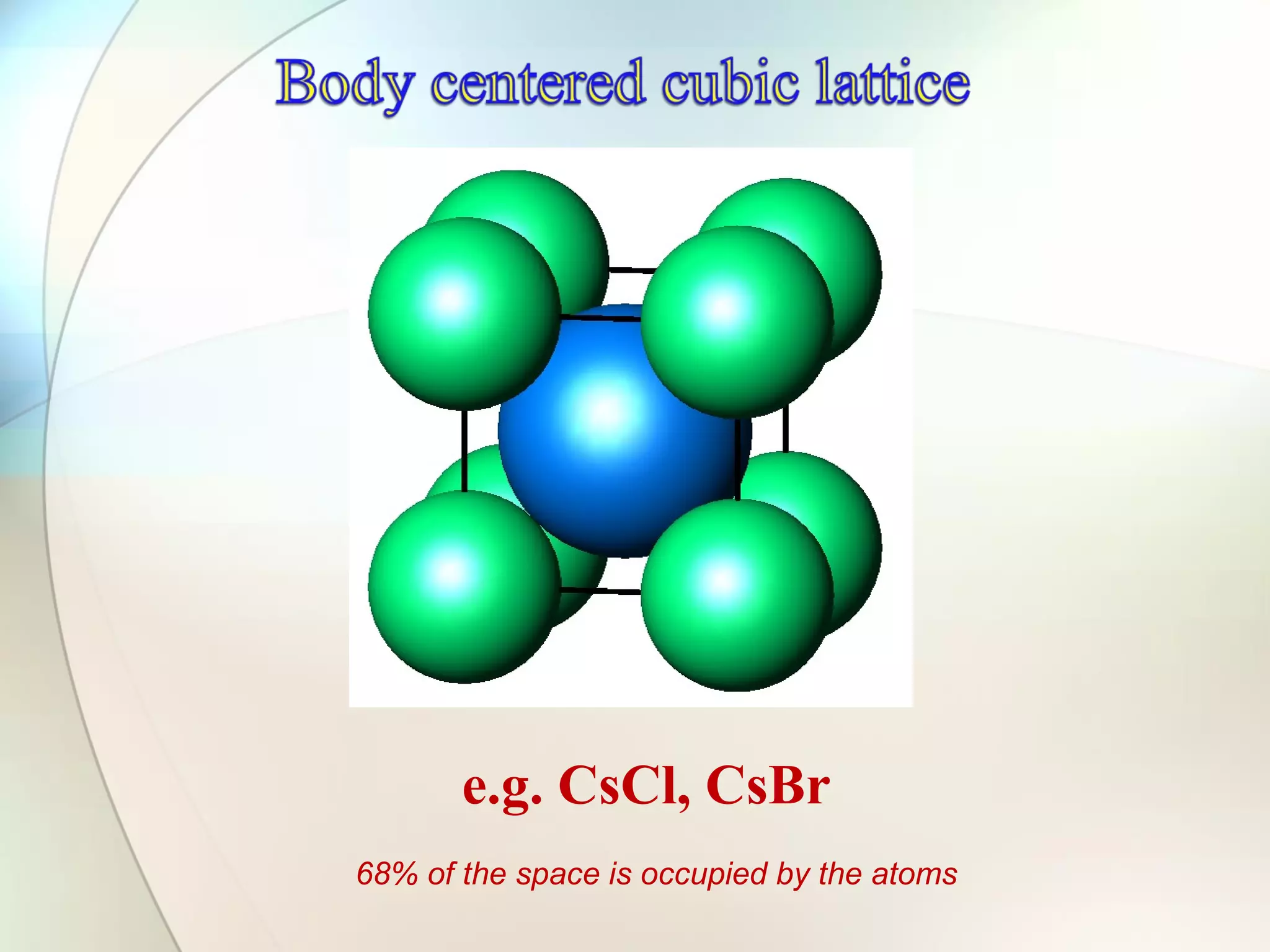
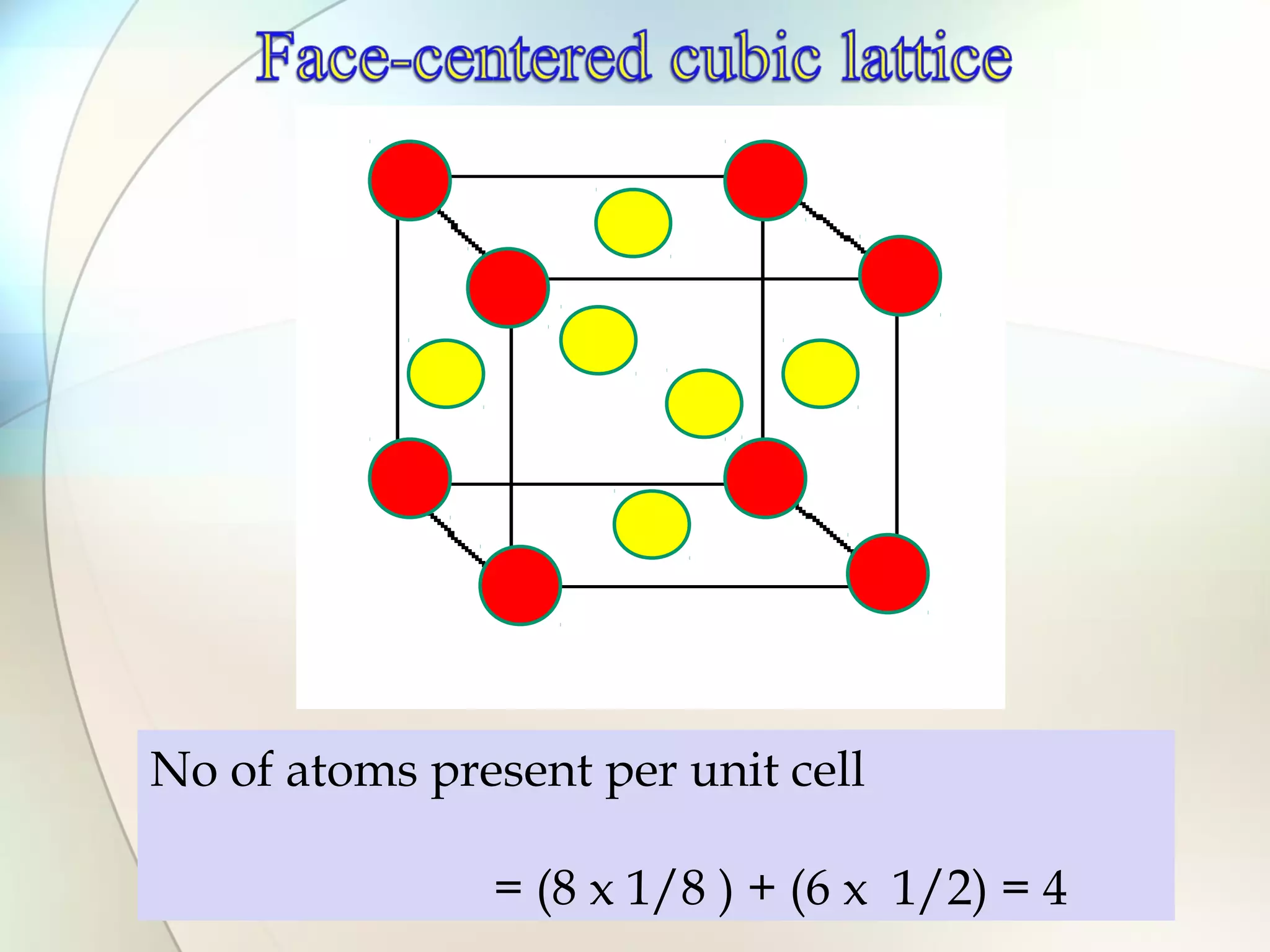
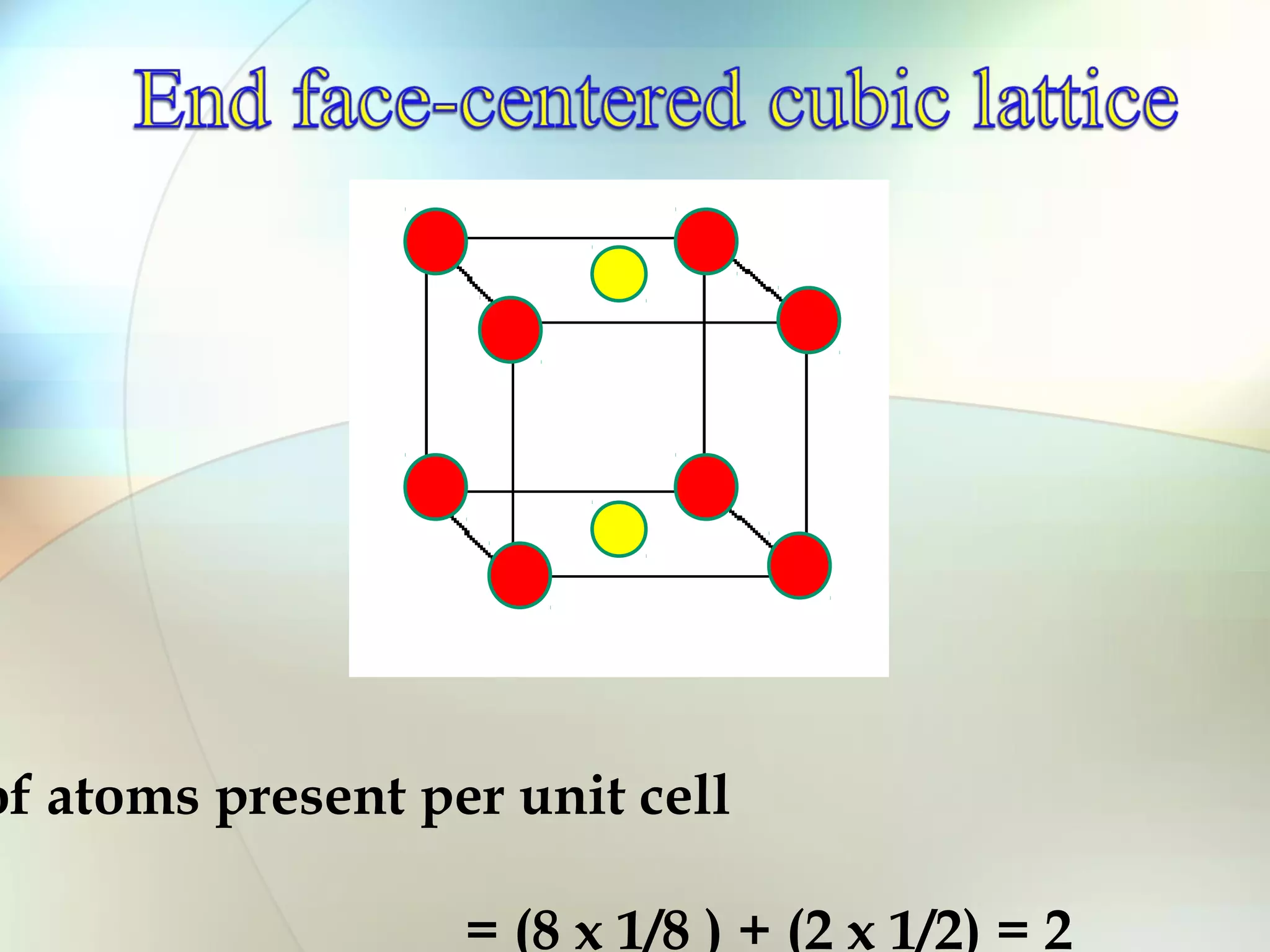
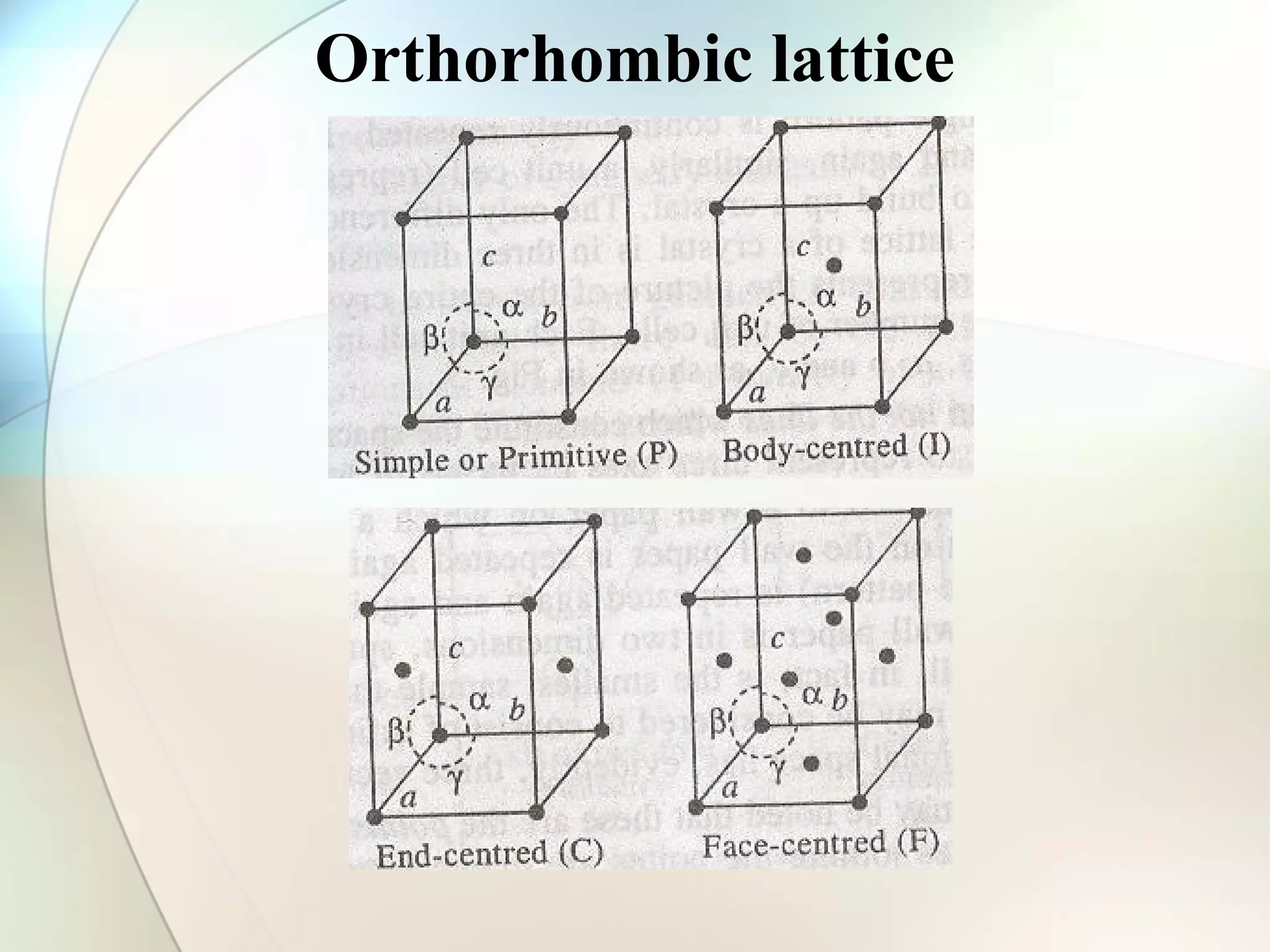
This document discusses solid state chemistry and provides information on various topics within the subject. It begins by defining the three states of matter and what distinguishes a solid. It then describes the two main types of solids - crystalline and amorphous - and provides details on their structures and properties. Various types of crystal structures are also outlined, including ionic, covalent, molecular and metallic crystals. The document concludes by discussing Bragg's equation and important solid materials like diamond, graphite and fullerenes.

1. SOLID STATE
CHEMISTRY

2. COnTEnTS
• Introduction
• Types of solids
• Crystal Structures
• Elements of Symmetry
• Bragg’s equation
• Allotropes of carbon: Diamond, graphite &
Fullerene

3. InTRODUCTIOn
Three phases of matter:
 Gas
 Liquid
 Solid

4. Gas
molecules
4

5. Liquid
molecules
5

6. Solid
molecules
6

7. WHAT IS SOLID?
• Definite shape.
• Definite volume.
• Highly incompressible.
• Rigid.
• Constituent particles held closely by strong
intermolecular forces.
• Fixed position of constituents.

8. TYPES OF SOLIDS
Two types (based upon atomic arrangement,
binding energy, physical & chemical
properties):
1.Crystalline
2. Amorphous

9. CRYSTALLInE SOLIDS
• The building constituents arrange themselves in regular
manner throughout the entire three dimensional network.
• Existence of crystalline lattice.
• A crystalline lattice is a solid figure which has a definite
geometrical shape, with flat faces and sharp edges.
• Incompressible orderly arranged units.
• Definite sharp melting point.
• Anisotropy.
• Definite geometry.
• Give x-ray diffraction bands.
• Examples: NaCl, CsCl, etc.

10. AMORPHOUS SOLIDS
• Derived from Greek word ‘Omorphe’ meaning
shapeless.
• No regular but haphazard arrangement of atoms or
molecules.
• Also considered as non-crystalline solids or super-
cooled liquids.
• No sharp m.p.
• Isotropic.
• No definite geometrical shape.
• Do not give x-ray diffraction bands.
• Examples: glass, rubber, plastics.

11. TYPES OF CRYSTAL STRUCTURES
• Ionic crystals
• Covalent crystals
• Molecular crystals
• Metallic crystals

12. IOnIC CRYSTALS
• Lattice points are occupied by positive and negative ions.
• Hard and brittle solids.
• High m.p. due to very strong electrostatic forces of
attraction.
• Poor conductors of electricity in solid state but good in
molten state.
• Packing of spheres depends upon:
 presence of charged species present.
 difference in the size of anions and cations.
• Two types:
 AB types.
 AB2 types.

13. COvALEnT CRYSTALS
• Lattice points are occupied by neutral atoms.
• Atoms are held together by covalent bonds
• Hard solids.
• High m.p.
• Poor conductors of electricity.
• Two common examples: diamond & graphite.

14. MOLECULAR CRYSTALS
• Lattice points are occupied by neutral molecules.
• The molecules are held together by vander
Waal’s forces.
• Very soft solids.
• Low m.p.
• Poor conductors of electricity.

15. METALLIC CRYSTALS
• Lattice points are occupied by positive metal ions
surrounded by a sea of mobile e-.
• Soft to very hard.
• Metals have high tensile strength.
• Good conductors of electricity.
• Malleable and ductile.
• Bonding electrons in metals remain delocalized over
the entire crystal.
• High density.

16. LAWS OF SYMMETRY
• Plane of symmetry
• Centre of symmetry
• Axis of symmetry.

17. ELEMEnTS OF SYMMETRY
In CUbIC CRYSTAL
• Rectangular planes of symmetry: 3
• Diagonal planes of symmetry: 6
• Axes of four-fold symmetry: 3
• Axes of three-fold symmetry: 4
• Axes of two-fold symmetry: 6
• Centre of symmetry: 1
Total symmetry elements: 23

18. Planes of symmetry
Rectangular plane of Diagonal plane of
symmetry: 3 symmetry: 6

19. axis of symmetry
Four-fold axis of Three-fold axis of
symmetry: 3 symmetry: 4

20. axis & centre of
symmetry
Two-fold axis of Centre of symmetry: 1
symmetry: 6

21. tyPes of cubic crystals
Four types:
1.Simple or primitive type
2. Body-centered
3. Face-centered
4. End face-centered

22. Simple or primitive type (sc) Body-centered cell (bcc)

23. Face-centered cell (fcc) End face-centered cell

24. number of atoms Per unit
cell in a cubic lattice
• Simple cubic cell: 1atom/unit cell of sc
• Body-centered cell: 2 atoms/unit cell of bcc
• Face-centered cell: 4 atoms/unit cell of fcc
• End face-centered cell: 2 atoms/unit cell

25. No of atoms per unit cell= 8 x 1/8 = 1

26. No of atoms per unit cell= 8 x 1/8 = 1

27. e.g.Polonium
52% of the space is occupied by the atoms

28. No of atoms present per unit cell
= (8 x 1/8 ) + (1 x 1) = 2

29. No of atoms per unit cell= (8 x 1/8) +1 = 2

30. e.g. CsCl, CsBr
68% of the space is occupied by the atoms

31. No of atoms present per unit cell
= (8 x 1/8 ) + (6 x 1/2) = 4

32. e.g. NaCl, NaF, KBr, MgO
74% of the space is occupied by the atoms

33. of atoms present per unit cell
= (8 x 1/8 ) + (2 x 1/2) = 2

34. atomic radius of a cubic lattice
• Simple cubic cell:
r = a/2
• Face-centered cubic cell:
r = a/√8
• Body-centered cubic cell:
r = √3a/4
(where a → length of cube)

35. Radius Ratio Rule
• Relation between the radius, co-ordination
number and the structural arrangement of the
molecule.
Radius ratio =
• Greater the radius ratio, larger the size of the
cation and hence the co-ordination number.
• density = (z*Ma)/Na*a^3 Ma=mass no.,
Na=avogadro, a= side length, z=no. of atoms

36. stRuctuRal analysis by
Radius Ratio Rule
S.NO. RADIUS CO-ORDINATION SHAPE EXAMPLE
RATIO NUMBER
1. 0.0 – 0.155 2 Linear HF-
2. 0.155–0.225 3 Triangular B2O3, BN
planar
3. 0.225– 0.414 4 Tetrahedral ZnS, SiO4-4
4. 0.414– 0.732 6 Octahedral NaCl
5. 0.732 – 1.0 8 Body-centered CsCl
cubic

37. bRaVais lattices
• Unit cell parameters:
 Lengths a, b & c.
 Angles α, β & γ.
• Total crystal lattices: 7
• Total Bravais lattices: 14

38. cRystal systems with unit
cell paRameteRs
S.No. System Cell Crystal Bravais Min. Sym.
Dimensions Angles Lattices Elements
1. Cubic a=b=c α=β=γ=90ْ sc, fcc, 3-fold axes: 4
bcc = 3 4-fold axes: 3
2. Orthorhombic a≠b≠c α=β=γ=90ْ sc, fcc, 2-fold axes: 3
bcc, efcc
=4
3. Tetragonal a=b≠c α=β=γ=90ْ sc, bcc= 2 4-fold axis: 1

39. S.No. System Cell Crystal Bravais Min. Sym.
Dimensions Angles Lattices Elements
4. Monoclinic a≠b≠c α = γ = 90ْ sc, efcc = 2 2-fold axis: 1
β ≠ 90ْ
5. Triclinic a≠b≠c α≠β≠γ≠ 90ْ sc = 1 1-fold axis: 1
6. Hexagonal a=b≠c α = β = 90ْ sc = 1 6-fold axis: 1
γ = 120ْ
7. Rhombohedral a=b=c α=β=γ≠ 90ْ sc = 1 3-fold axis: 1
or Trigonal

40. examples of diffeRent
cRystal systems
S.No. System Example
1. Cubic NaCl, KCl, CaF2, Cu, ZnS, CsCl, Cu2O
2. Orthorhombic BaSO4, KNO3, MgSiO3, K2SO4, CdSO4,
AgBr
3. Tetragonal SnO2, TiO2, ZrSiO4
4. Monoclinic CaSO4.2H2O, monoclinic S
5. Triclinic CuSO4.5H2O, NaHSO4, H3PO3
6. Hexagonal PbI2, Mg, Cd, Zn, ZnO, BN, SiO2, HgS,
CdS
7. Rhombohedral or Trigonal Graphite, ICl, Al2O3, calcite (CaCO3), As,
Sb, Bi

41. Cubic lattice

42. Orthorhombic lattice

43. Tetragonal lattices

44. Monoclinic lattice

45. Triclinic lattice

46. Hexagonal lattice

47. Rhombohedral (Trigonal) lattice

48. stRuctuRes of impoRtant
ionic compounds
1. AB type: NaCl (rock salt)
CsCl
ZnS (zinc blende / sphalerite)
2. AB2 type: CaF2 (fluorite)
TiO2 (rutile)
SiO2

49. Structure of NaCl (Rock salt)
• FCC type.
• Co-ordination number 6:6.
• Calculation of no. of atoms of NaCl/unit
cell:
Cl at corners: (8 × 1/8) =1
Cl at face centres (6 × 1/2) =3
Na at edge centres (12 × 1/4) = 3
Na at body centre =1
Unit cell contents are 4(Na+Cl-)
i.e. per each unit cell, 4 NaCl
units will be present.

50. stRuctuRe of sodium
choRide
Cubic unit cell:
smallest repeatable unit

51. Structure of CsCl
• bcc type.
• Co-ordination number 8:8.
• Number of atoms/unit cell:1

52. Structure of ZnS
• fcc type.
• Co-ordination number
4:4.
• Calculation of no. of
atoms/unit cell:
Total S = 8x1/8 + 6x1/2 = 4
Total Zn = 4
Hence, total ZnS = 4

53. Structure of CaF2
Ca+
F-
• fcc type.
• Co-ordination number: 8:4
(8 for cation, 4 for anion)
*Note: All the compounds of AB2 type follow the same pattern.

54. Structure of K2O
O -2
Na+
• fcc type.
• Co-ordination number: 4:8
4 for cation
8 for anion

55. Structure of important
covalent compoundS
1.Diamond
2. Graphite

56. Diamond

57. Structure of diamond
• fcc type.
• Tetrahedral
• C-C bond length = 1.34A
• Refractive index = 2.4
• High dispersive power of light
• Non-conductor of electricity
• 3d network
• Hardest substance ever known.
• Used as abrasive.

58. 3d- structure of diamond

59. Graphite

60. Structure of Graphite
• One of the softest substances ever known.
• 2-d hexagonal layer structure
• C-C bond length = 1.45A
• Inter layer distance = 3.54A
• Sliding nature
• sp2 hybridisation with one electron left over.
• Specific gravity 2.2
• Electrical conductor
• Metallic lustre
• Used as good lubricant.

61. 2d- structure of graphite

62. fullureneS

63. Important points about Fullurenes
• Discovered in 1985 as C60.
• Consists of spherical, ellipsoid or cylindrical
arrangement of dozens of C-atoms.
• 3 types:
 Spherical: Also called ‘bucky balls’. Molecule
of the year 1991 by Science magazine.
 Cylindrical: C nanotubes or buckytubes.
 Planar.

64. Structure of fullurenes
• 60 C-atoms arranged in pentagons and hexagons.
• 7Å in diameter.
• Soccer-ball shaped molecule with 20 six-membered & 12
five-membered rings.
• Each pentagon is surrounded by five hexagons.
• No two pentagons are adjecent.
• Each carbon is sp2-hybridized.
• Used:
 as photoresistant.
 in the preparation of super-conductors.
 in optical devices.
 in batteries as charge carriers.

65. BraGG’S eQuation
X-ray
Tube Detector
Incident radiation “Reflected” radiation 1
2
θ θ
X Z
Y
d
Transmitted radiation
Beam 2 lags beam 1 by XYZ = 2d sin θ
so 2d sin θ = nλ Bragg’s Law