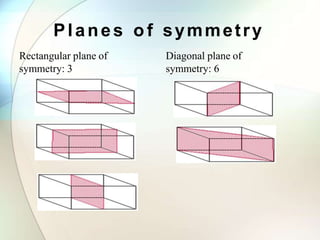
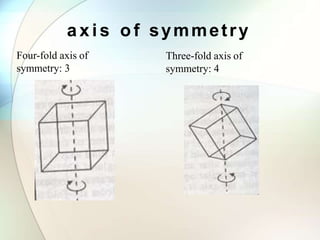
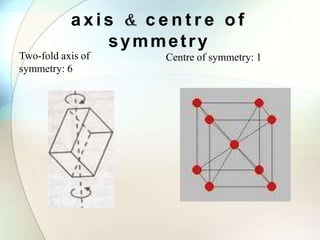
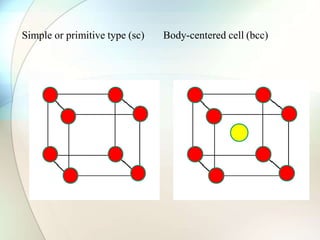
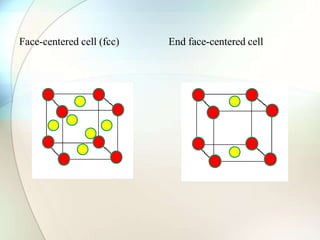
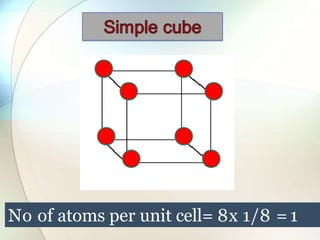
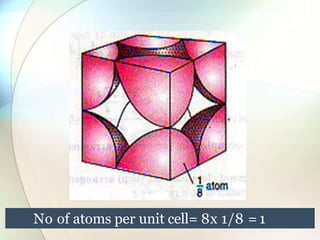
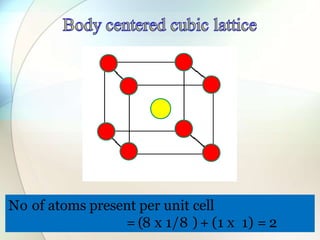
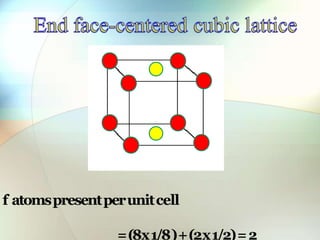
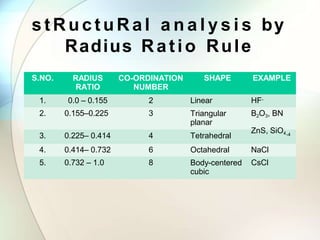
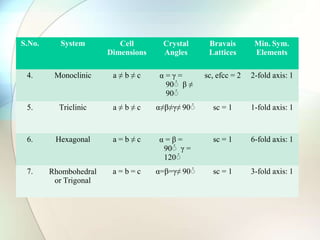
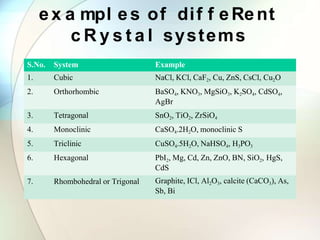
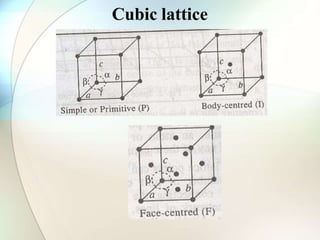
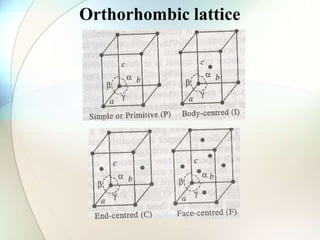
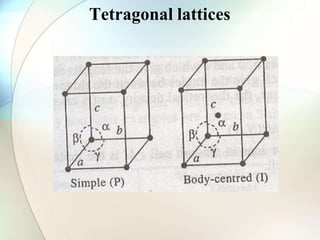
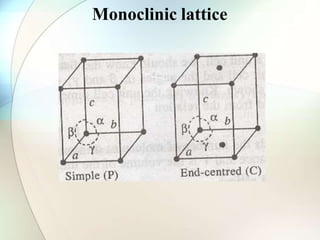
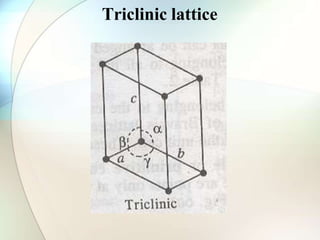
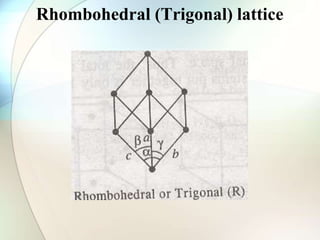
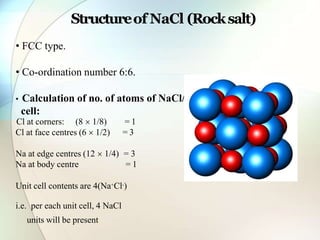
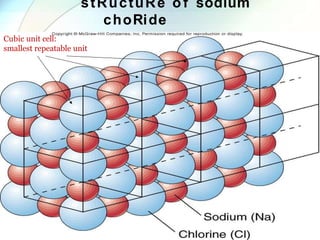
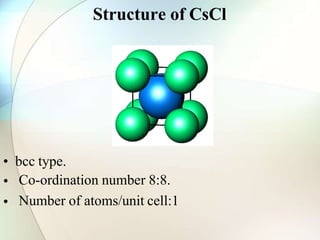
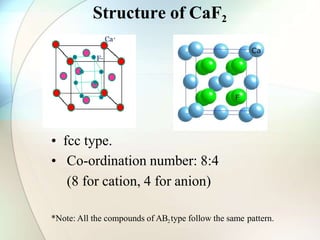
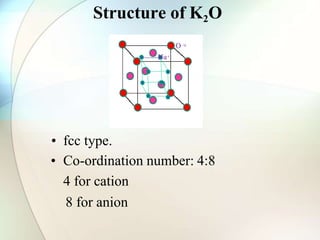
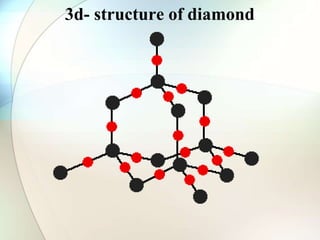
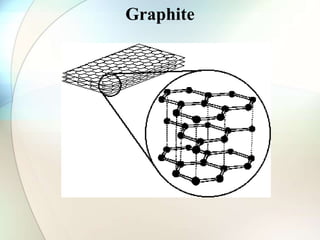
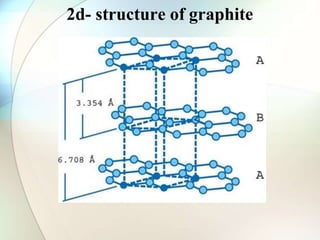
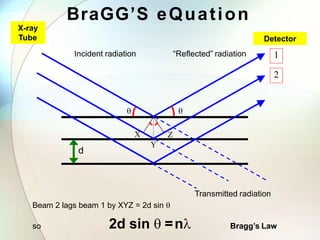
This document provides a summary of key topics in solid state chemistry, including the three phases of matter, types of solids (crystalline and amorphous), crystal structures (ionic, covalent, molecular, metallic), symmetry elements, Bragg's equation, and allotropes of carbon (diamond, graphite, fullerene). It describes characteristics of each topic in 1-3 sentences, with accompanying diagrams and examples. Key definitions include crystalline lattices, unit cells, coordination numbers, radius ratio rule for predicting structure, and the seven crystal systems.

1. Class - 12th
Sub: Chemistry
Topic: Solid State
Prepared by:
Aditya Prashar

2. SOLID STATE
CHEMISTRY

3. CONTENTS
• Introduction
• Types of solids
• Crystal Structures
• Elements of Symmetry
• Bragg’s equation
• Allotropes of carbon: Diamond, graphite &
Fullerene

4. INTRODUCTION
Three phases of matter:
Gas
Liquid
Solid

5. Gas
molecules
4

6. Liquid
molecules
5

7. Solid
molecules
6

8. WHAT IS SOLID
• Definite shape.
•
•
•
•
•
Definite volume.
Highly incompressible.
Rigid.
Constituent particles held closely by strong
intermolecular forces.
Fixed position of constituents.

9. TYPES OF SOLIDS
Two types (based upon atomic arrangement,
binding energy, physical & chemical
properties):
1.Crystalline
2. Amorphous

10. CRYSTALLINE SOLIDS
•
•
•
•
•
•
•
•
•
The building constituents arrange themselves in regular
manner throughout the entire three dimensional network.
Existence of crystalline lattice.
A crystalline lattice is a solid figure which has a definite
geometrical shape, with flat faces and sharp edges.
Incompressible orderly arranged units.
Definite sharp melting point.
Anisotropy.
Definite geometry.
Give x-ray diffraction bands.
Examples: NaCl, CsCl, etc.

11. AMORPHOUS SOLIDS
• Derived from Greek word ‘Omorphe’ meaning
shapeless.
• No regular but haphazard arrangement of atoms or
molecules.
• Also considered as non-crystalline solids or super-
cooled liquids.
• No sharp m.p.
• Isotropic.
• No definite geometrical shape.
• Do not give x-ray diffraction bands.
• Examples: glass, rubber, plastics.

12. TYPES OF CRYSTAL STRUCTURES
•
•
•
•
Ionic crystals
Covalent crystals
Molecular crystals
Metallic crystals

13. IONIC CRYSTALS
•
•
•
•
•
Lattice points are occupied by positive and negative ions.
Hard and brittle solids.
High m.p. due to very strong electrostatic forces of
attraction.
Poor conductors of electricity in solid state but good in
molten state.
Packing of spheres depends upon:
presence of charged species present.
difference in the size of anions and cations.
• Two types:
AB types.
AB2types.

14. COvALEnT CRYSTALS
•
•
Lattice points are occupied by neutral atoms.
Atoms are held together by covalent bonds
• Hard solids.
•
•
•
High m.p.
Poor conductors of electricity.
Two common examples: diamond & graphite.

15. MOLECULAR CRYSTALS
• Lattice points are occupied by neutral molecules.
• The molecules are held together by vander
Waal’s forces.
• Very soft solids.
•
•
Low m.p.
Poor conductors of electricity.

16. METALLIC CRYSTALS
• Lattice points are occupied by positive metal ions
surrounded by a sea of mobile e-.
• Soft to very hard.
•
•
•
•
•
Metals have high tensile strength.
Good conductors of electricity.
Malleable and ductile.
Bonding electrons in metals remain delocalized over
the entire crystal.
High density.

17. LAWS OF SYMMETRY
• Plane of symmetry
• Centre of symmetry
• Axis of symmetry.

18. ELEMEnTS OF SYMMETRY
In CUbIC CRYSTAL
•
•
•
•
•
•
Rectangular planes of symmetry: 3
Diagonal planes of symmetry: 6
Axes of four-fold symmetry: 3
Axes of three-fold symmetry: 4
Axes of two-fold symmetry: 6
Centre of symmetry: 1
Total symmetry elements: 23

19. Planes o f symmetry
Rectangular plane of
symmetry: 3
Diagonal plane of
symmetry: 6

20. a x i s o f symmetry
Four-fold axis of
symmetry: 3
Three-fold axis of
symmetry: 4

21. a x i s c e n t r e o f
Two-fold axis of
symmetry: 6
symmetry
Centre of symmetry: 1

22. T Y P E S O F CUBIC C R Y S T A L S
Four types:
1.Simple or primitive type
2. Body-centered
3. Face-centered
4. End face-centered

23. Simple or primitive type (sc) Body-centered cell (bcc)

24. Face-centered cell (fcc) End face-centered cell

25. NUMBER O F A T O M S P E R U N I T
C E L L IN A CUBIC L A T T I C E
• Simple cubic cell: 1atom/unit cell of sc
•
•
•
Body-centered cell: 2 atoms/unit cell of bcc
Face-centered cell: 4 atoms/unit cell of fcc
End face-centered cell: 2 atoms/unit cell

26. No of atoms per unit cell= 8x 1/8 =1

27. No of atoms per unit cell= 8x 1/8 = 1

28. e.g.Polonium
52% of the space is occupied by the atoms

29. No of atoms present per unit cell
= (8 x 1/8 ) + (1 x 1) = 2

30. No of atoms per unit cell= (8x 1/8) +1 =2

31. e.g. CsCl, CsBr
68% of the space is occupied by the atoms

32. No of atoms present per unit cell
= (8 x 1/8 ) + (6 x 1/2) = 4

33. e.g. NaCl, NaF, KBr, MgO
74% of the space is occupied by the atoms

34. f atomspresentperunitcell
=(8x1/8)+(2x1/2)=2

35. A T O M I C R A D I U S O F A CUBIC L A T T I C E
• Simple cubic cell:
r = a/2
• Face-centered cubic cell:
r = a/√8
• Body-centered cubic cell:
r = √3a/4
(where a → length of cube)

36. Ra dius Ra t i o Rul e
• Relation between the radius, co-ordination
number and the structural arrangement of the
molecule.
Radius ratio =
• Greater the radius ratio, larger the size of the
cation and hence the co-ordination number.
•density = (z*Ma)/Na*a^3 Ma=mass no.,
Na=avogadro, a= side length, z=no. of atoms

37. Coordination Number (CN) :
The number of spheres (atoms, molecules
or ions) directly surrounding a single
sphere in a crystal, is called coordination
number.
E.g

38. The radius of calcium ion is 94 pm and that of an
oxide ion is 146 pm. Find the coordination
number of calcium?
Given: Radius of cation (r+ ) = 94 pm Radius of
anion (r– ) = 146pm
To find: The coordination number of calcium = ?
Formula: Radius ratio = Radiusof the cation/
Radius of the anion
Calculation: From formula,
Radius ratio = r+ /r − = 94 /146 = 0.6438
Since the radius ratio lies in between 0.414 –
0.732
The coordination number of calcium is 6.

39. s t R u c t u R a l a n a l y s i s by
Radius Ratio Rule
S.NO. RADIUS
RATIO
CO-ORDINATION
NUMBER
SHAPE EXAMPLE
1. 0.0 – 0.155 2 Linear HF-
2. 0.155–0.225 3 Triangular
planar
B2O3, BN
3. 0.225– 0.414 4 Tetrahedral
ZnS, SiO4-4
4. 0.414– 0.732 6 Octahedral NaCl
5. 0.732 – 1.0 8 Body-centered
cubic
CsCl

40. bRaVais l a t t i c e s
• Unit cell parameters:
Lengths : a, b & c.
Angles: α, β & γ.
• Total crystal lattices: 7
• Total Bravais lattices: 14

41. c R y s t a l systems with unit
c e l l paRameteRs
S.No. System Cell
Dimensions
Crystal
Angles
Bravais
Lattices
Min. Sym.
Elements
1. Cubic a = b = c α=β=γ=90ْ sc, fcc,
bcc = 3
3 fold axes: 4
4 fold axes: 3
2. Orthorhombic a ≠ b ≠ c α=β=γ=90ْ sc, fcc,
bcc, efcc
= 4
2-fold axes: 3
3. Tetragonal a = b ≠ c α=β=γ=90ْ sc, bcc= 2 4-fold axis: 1

42. S.No. System Cell
Dimensions
Crystal
Angles
Bravais
Lattices
Min. Sym.
Elements
4. Monoclinic a ≠ b ≠ c α = γ =
90ْ β ≠
90ْ
sc, efcc = 2 2-fold axis: 1
5. Triclinic a ≠ b ≠ c α≠β≠γ≠ 90ْ sc = 1 1-fold axis: 1
6. Hexagonal a = b ≠ c α = β =
90ْ γ =
120ْ
sc = 1 6-fold axis: 1
7. Rhombohedral
or Trigonal
a = b = c α=β=γ≠ 90ْ sc = 1 3-fold axis: 1

43. ex a mpl es of dif f eRent
c R y s t a l systems
S.No. System Example
1. Cubic NaCl, KCl, CaF2, Cu, ZnS, CsCl, Cu2O
2. Orthorhombic BaSO4, KNO3, MgSiO3, K2SO4, CdSO4,
AgBr
3. Tetragonal SnO2, TiO2, ZrSiO4
4. Monoclinic CaSO4.2H2O, monoclinic S
5. Triclinic CuSO4.5H2O, NaHSO4, H3PO3
6. Hexagonal PbI2, Mg, Cd, Zn, ZnO, BN, SiO2, HgS,
CdS
7. Rhombohedral or Trigonal Graphite, ICl, Al2O3, calcite (CaCO3), As,
Sb, Bi

44. Cubic lattice

45. Orthorhombic lattice

46. Tetragonal lattices

47. Monoclinic lattice

48. Triclinic lattice

49. Hexagonal lattice

50. Rhombohedral (Trigonal) lattice

51. st Ruct uRes of impoRt a nt
ionic compounds
1. AB type: NaCl (rock salt)
CsCl
ZnS (zinc blende / sphalerite)
2. AB2type: CaF2 (fluorite)
TiO2 (rutile)
SiO2

52. uni
t
• FCC type.
• Co-ordination number 6:6.
• Calculation of no. of atoms of NaCl/
cell:
Cl at face centres (6  1/2)
Cl at corners: (8  1/8) = 1
= 3
Na at edge centres (12  1/4) = 3
Na at body centre = 1
Unit cell contents are 4(Na+Cl-)
i.e. per each unit cell, 4 NaCl
units will be present.
Structureof NaCl (Rocksalt)

53. stRuctuRe o f sodium
choRide
Cubic unit cell:
smallest repeatable unit

54. Structure of CsCl
• bcc type.
•
•
Co-ordination number 8:8.
Number of atoms/unit cell:1

55. Structure of ZnS
• fcc type.
• Co-ordination number
•
4:4.
Calculation of no. of
atoms/unit cell:
Total S = 8x1/8 + 6x1/2 = 4
Total Zn = 4
Hence, total ZnS = 4

56. Structure of CaF2
• fcc type.
• Co-ordination number: 8:4
(8 for cation, 4 for anion)
*Note: All the compounds of AB2type follow the same pattern.
Ca+
F-

57. Structure of K2O
• fcc type.
• Co-ordination number: 4:8
4 for cation
8 for anion
O -2
Na+

58. S t r u c t u r e o f i m p o r t a n t
c o v a l e n t compoundS
1.Diamond
2. Graphite

59. Diamond

60. Structure of diamond
• fcc type.
• Tetrahedral
• C-C bond length = 1.34A
• Refractive index = 2.4
• High dispersive power of light
• Non-conductor of electricity
• 3d network
•
•
Hardest substance ever known.
Used as abrasive.

61. 3d- structure of diamond

62. Graphite

63. Structure of Graphite
• One of the softest substances ever known.
• 2-d hexagonal layer structure
• C-C bond length = 1.45A
• Inter layer distance = 3.54A
• Sliding nature
• sp2hybridisation with one electron left over.
• Specific gravity 2.2
• Electrical conductor
• Metallic lustre
• Used as good lubricant.

64. 2d- structure of graphite

65. f u l l u r e n e S

66. Important points about Fullurenes
•
• Discovered in 1985 as C60.
• Consists of spherical, ellipsoid or cylindrical
arrangement of dozens of C-atoms.
3 types:
Spherical: Also called ‘bucky balls’. Molecule
of the year 1991 by Science magazine.
Cylindrical: C nanotubes or buckytubes.
Planar.

67. Structure of fullurenes
•
•
•
•
•
•
•
60 C-atoms arranged in pentagons and hexagons.
7Å in diameter.
Soccer-ball shaped molecule with 20 six-membered & 12
five-membered rings.
Each pentagon is surrounded by five hexagons.
No two pentagons are adjecent.
Each carbon is sp2-hybridized.
Used:
as photoresistant.
in the preparation of super-conductors.
in optical devices.
in batteries as charge carriers.

68. BraGG’S eQuation
X
Y
Z
d
Incident radiation “Reflected” radiation
 
1
2
X-ray
Tube Detector
Transmitted radiation
Beam 2 lags beam 1 by XYZ = 2d sin 
so 2d sin  =n Bragg’s Law

69. Home Assignment
Sodium metal crystallizes in body
centered cubic lattice with cell edge =
4.29 Å. What is the radius of sodium
atom?
In silicates the oxygen atom forms a
tetrahedral void. The limiting radius ratio
for tetrahedral void is 0.22. The radius of
oxide is 1.4 Å. Find out the radius of
cation.

70. THANK
YOU
PLEASE OBEY THE
RULES OF LOCKDOWN
STAY HOME STAY SAFE