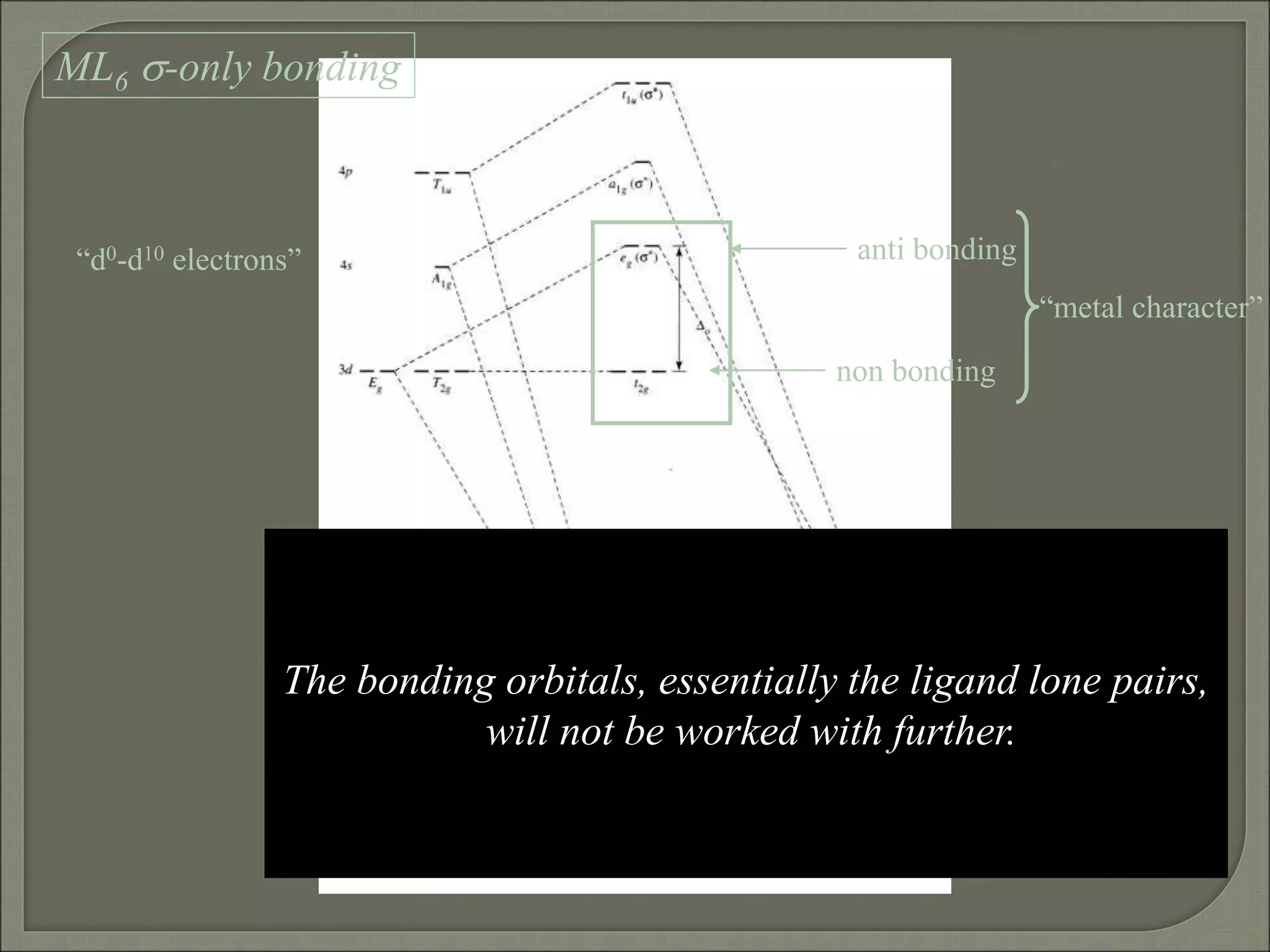
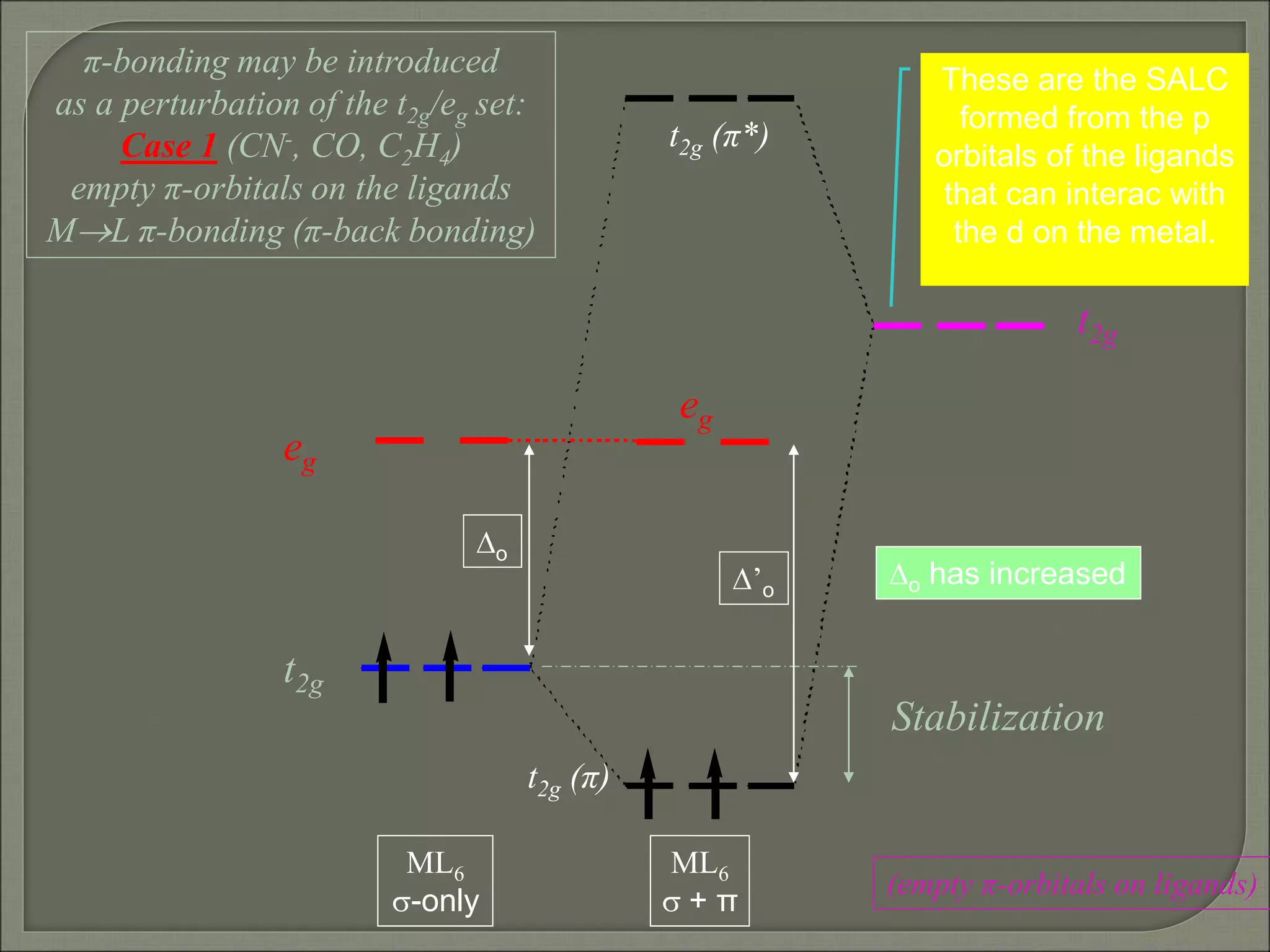
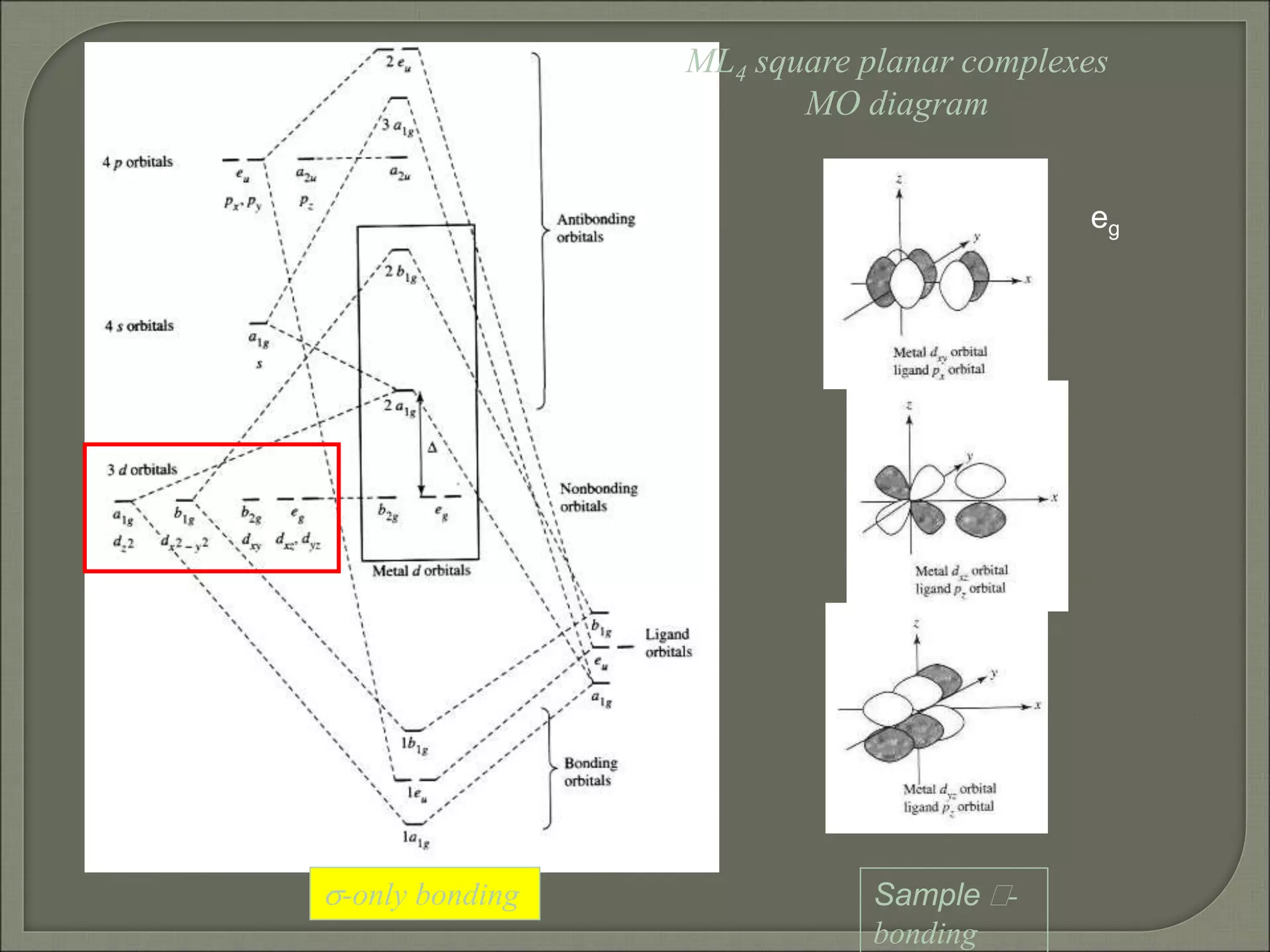
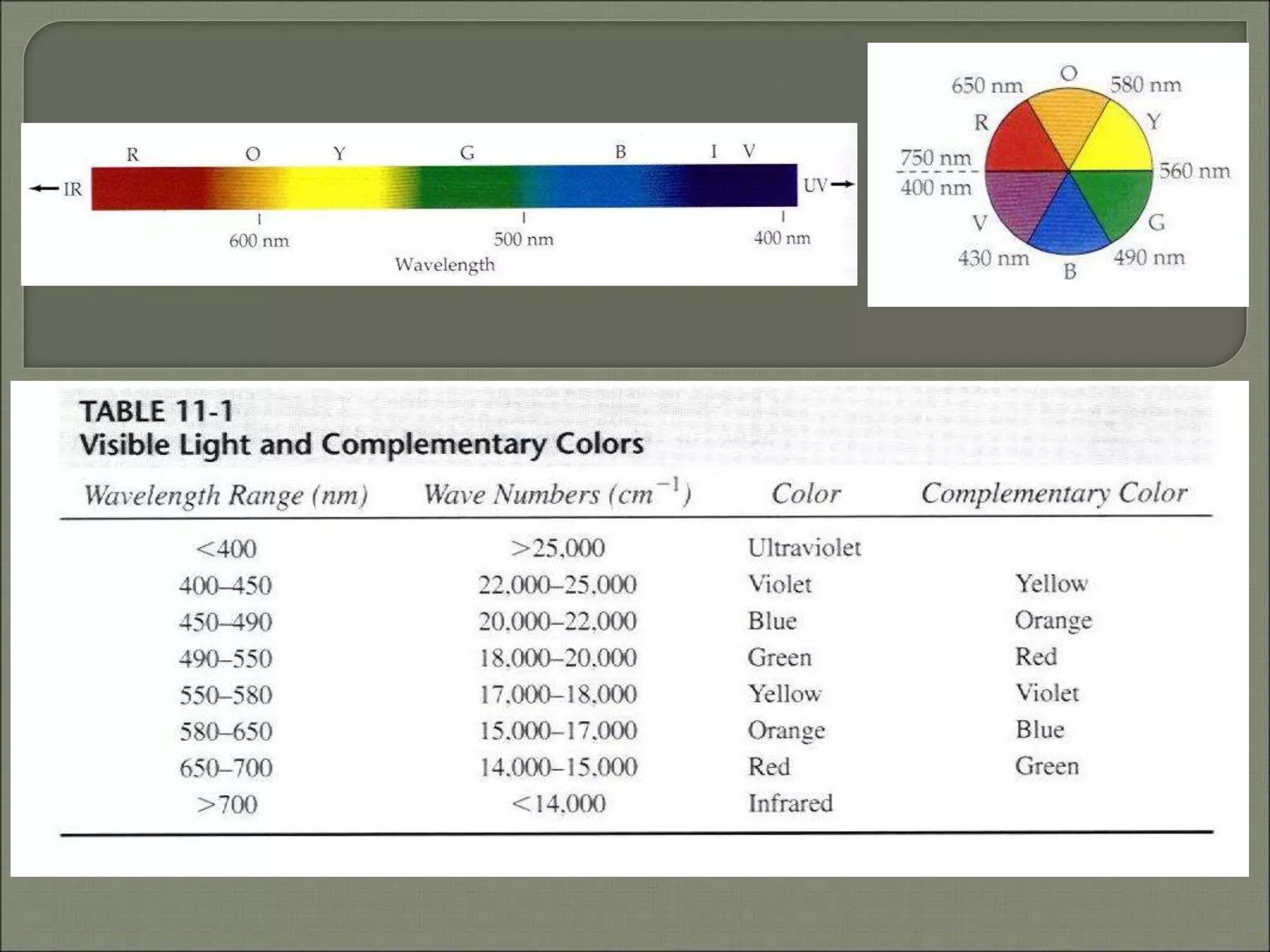
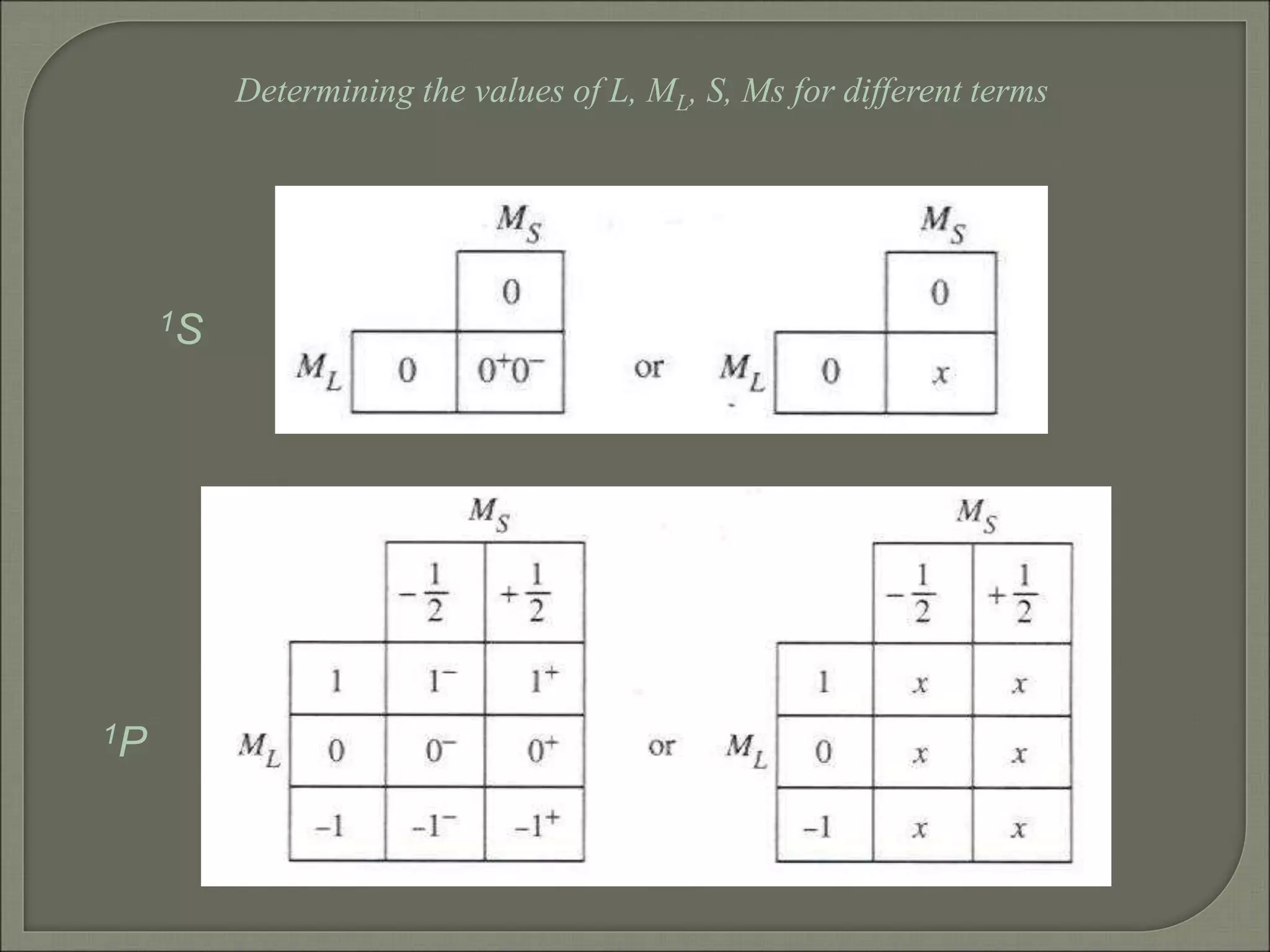
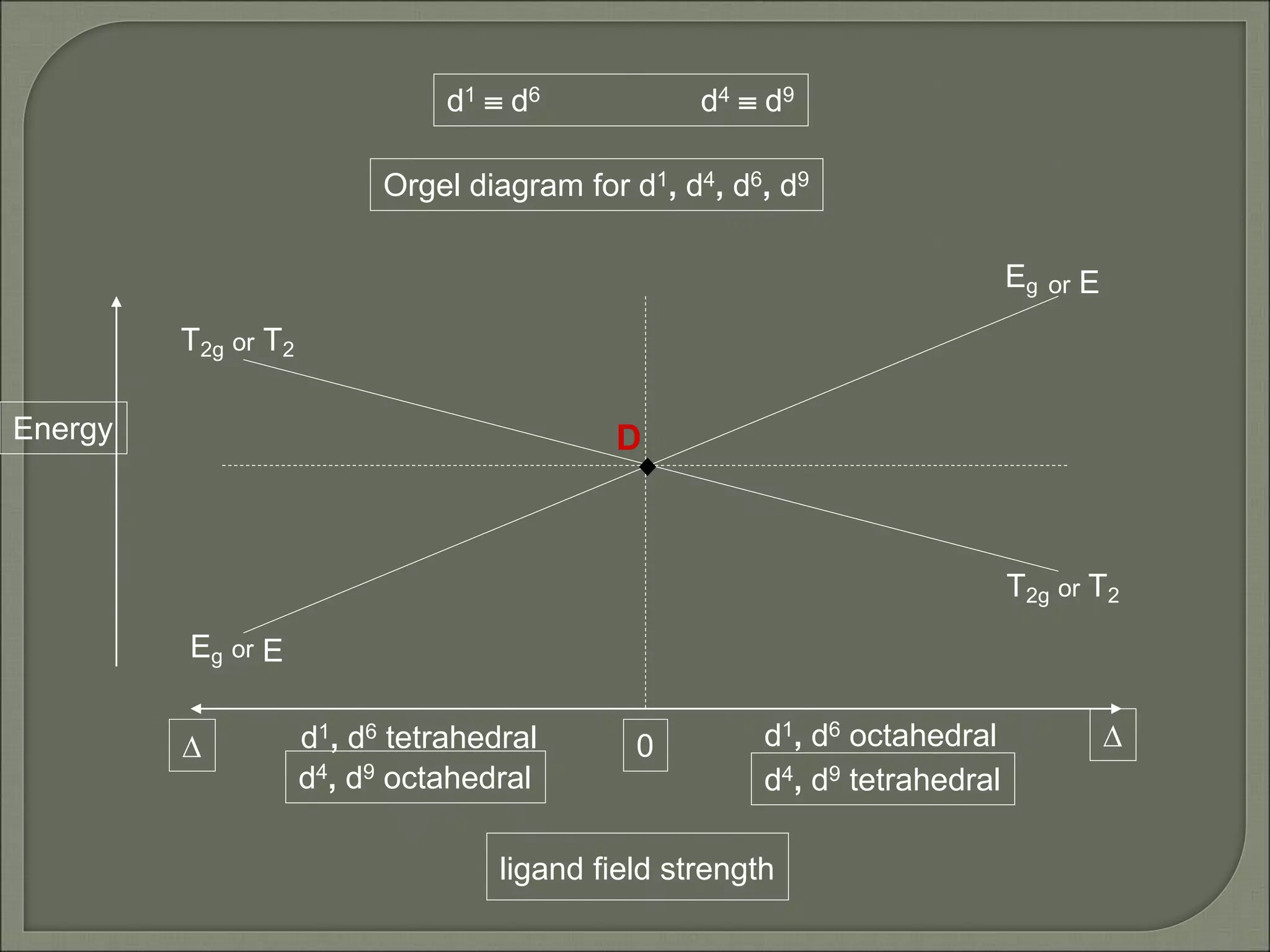
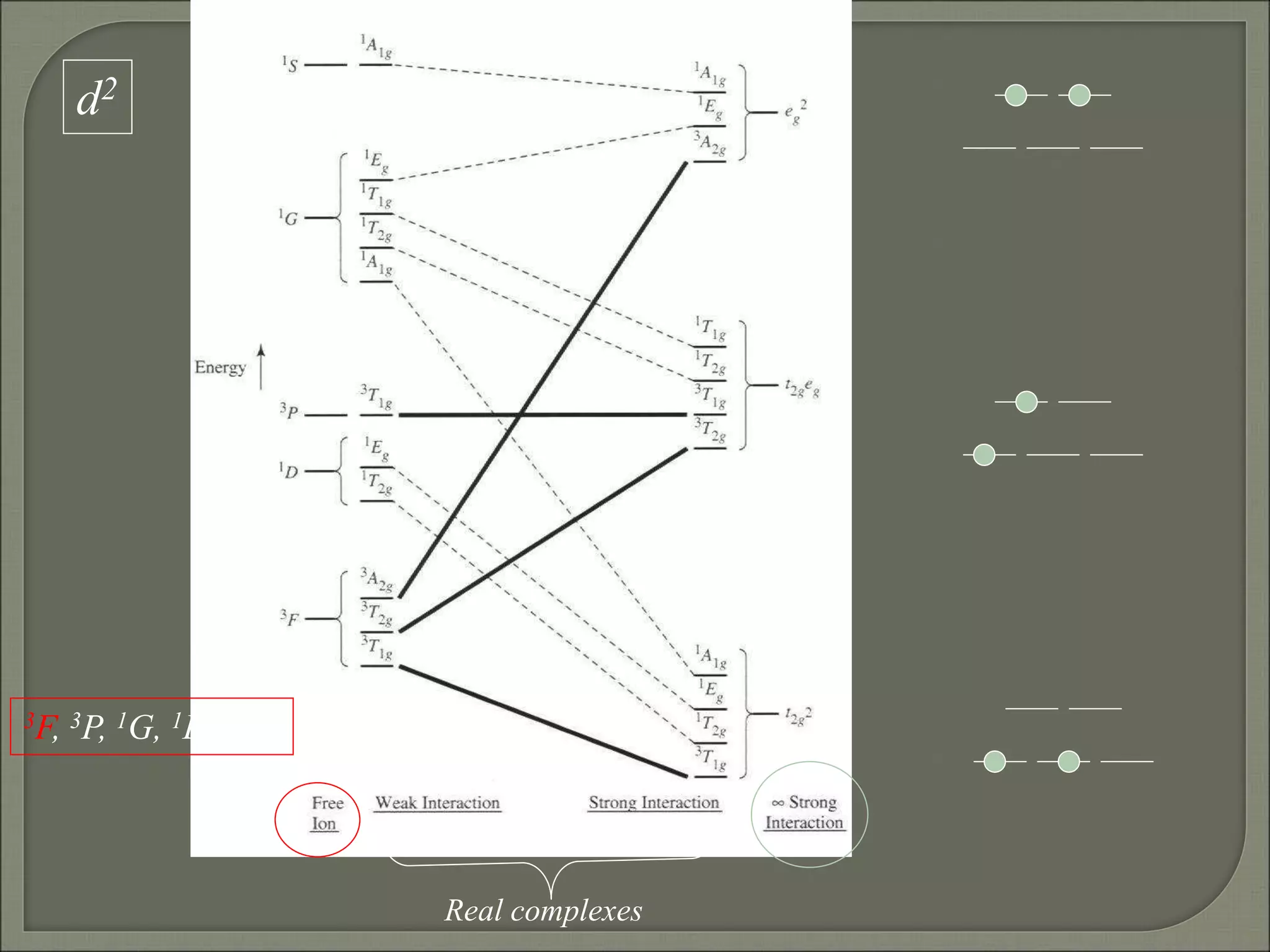
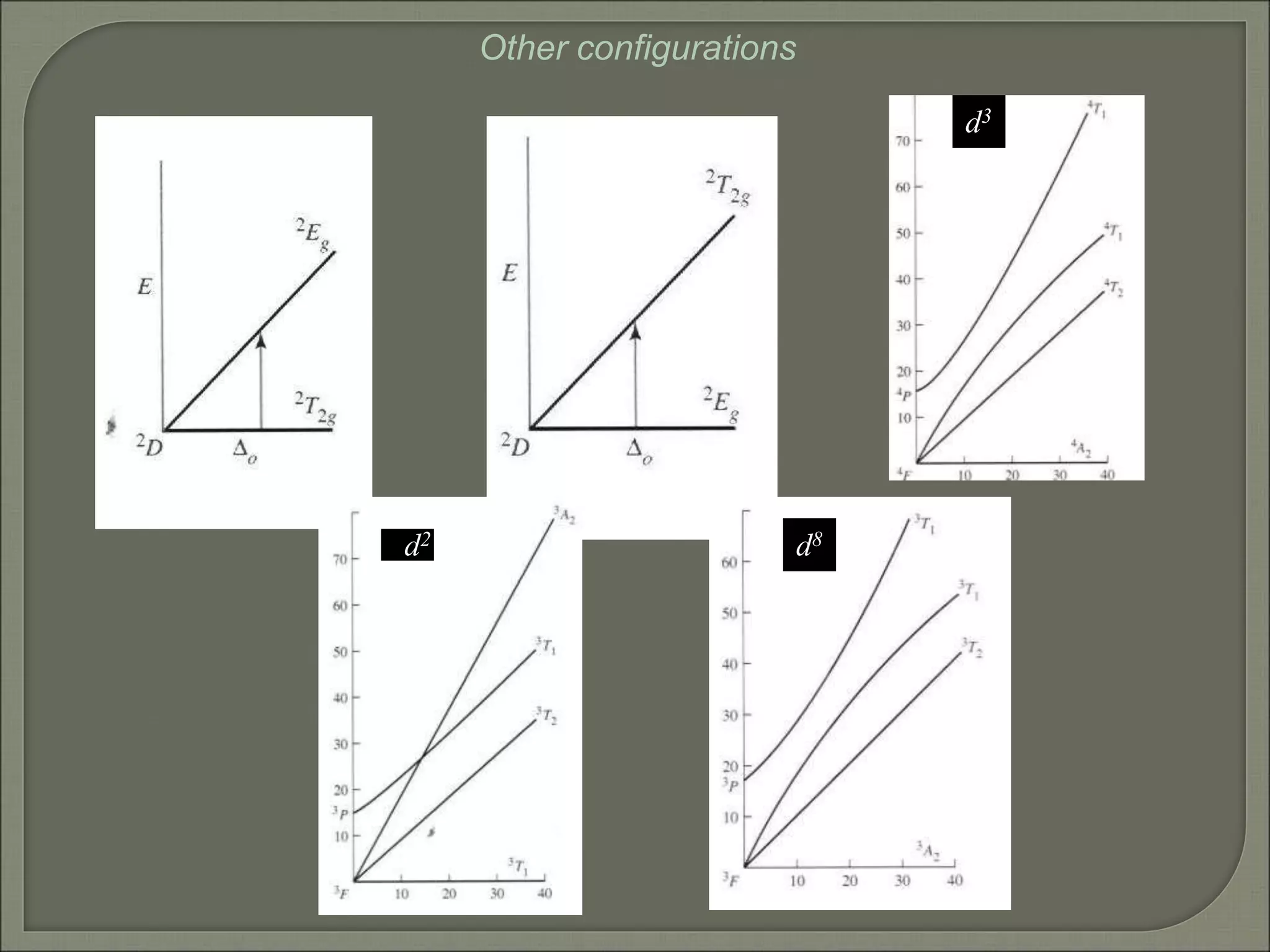
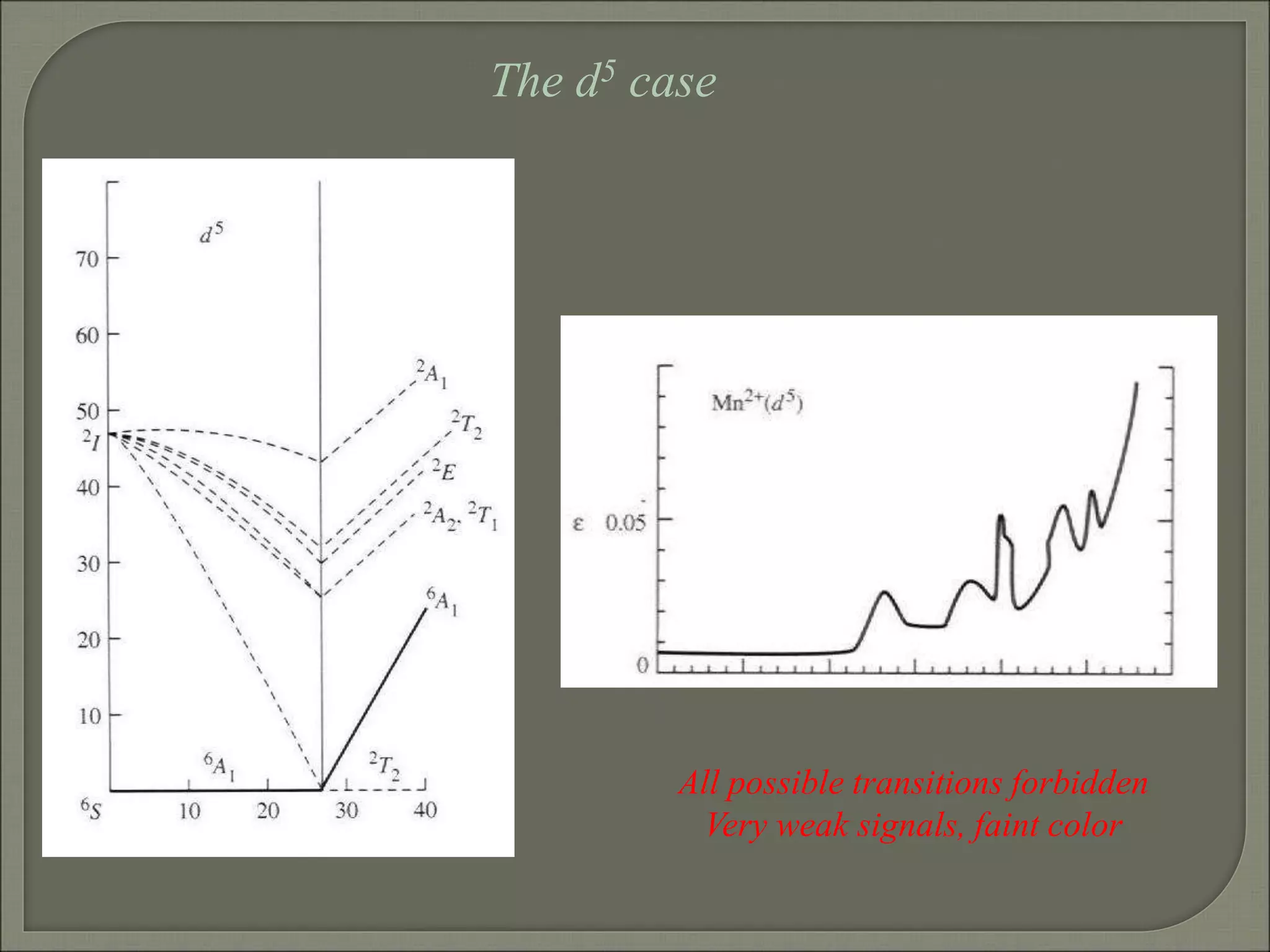
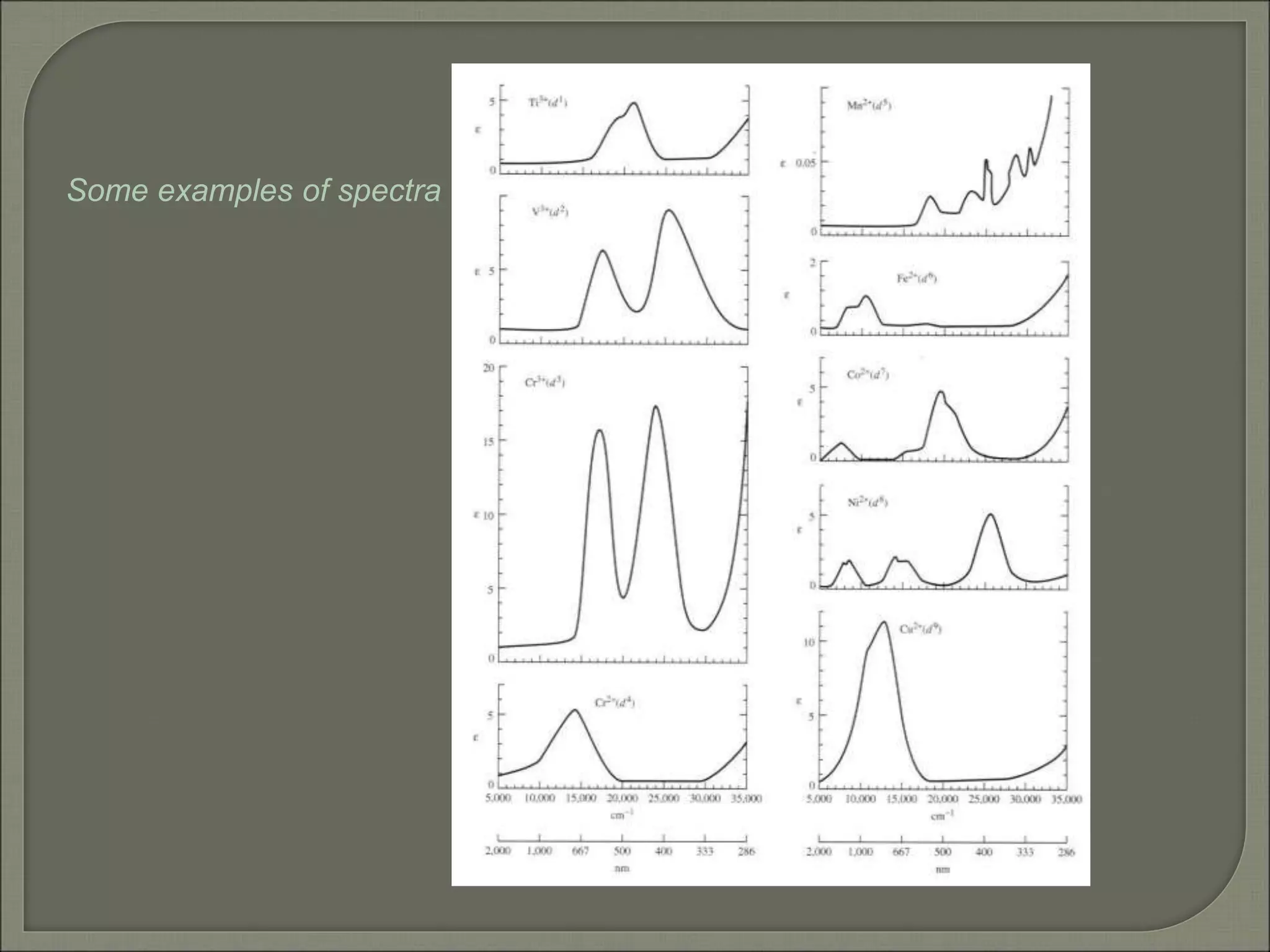
This document discusses the electronic structure and spectra of metal complexes. It begins by introducing ligand field theory and how the d orbitals of the metal ion split into different energy levels depending on the geometry and ligand field strength. Orgel diagrams are used to illustrate the splitting patterns for different d electron configurations from d1 to d10. Selection rules for electronic transitions are described. Tanabe-Sugano diagrams show how transition energies vary with ligand field strength. Methods for determining the ligand field splitting parameter (Δo) from experimental spectra are also outlined, along with examples of different types of spectra observed.

1. SARAH TUCKER COLLEGE
TIRUNELVELI.

2. 6 s ligands x 2e each
12 s bonding e
“ligand character”
“d0-d10 electrons”
non bonding
anti bonding
“metal character”
ML6 s-only bonding
The bonding orbitals, essentially the ligand lone pairs,
will not be worked with further.

3. t2g
eg
t2g
ML6
s-only
ML6
s + π
Stabilization
(empty π-orbitals on ligands)
Do
D’o
Do has increased
π-bonding may be introduced
as a perturbation of the t2g/eg set:
Case 1 (CN-, CO, C2H4)
empty π-orbitals on the ligands
ML π-bonding (π-back bonding)
t2g (π)
t2g (π*)
eg
These are the SALC
formed from the p
orbitals of the ligands
that can interac with
the d on the metal.

4. t2g
eg
t2g
ML6
s-only
ML6
s + π
π-bonding may be introduced
as a perturbation of the t2g/eg set.
Case 2 (Cl-, F-)
filled π-orbitals on the ligands
LM π-bonding
(filled π-orbitals)
Stabilization
Destabilization
t2g (π)
t2g (π*)
eg
D’o
Do
Do has decreased

5. Strong field / low spin Weak field / high spin
Putting it all on one
diagram.

6. Purely s ligands:
D: en > NH3 (order of proton basicity)
 donating which decreases splitting and causes high spin:
D: H2O > F > RCO2 > OH > Cl > Br > I (also proton basicity)
 accepting ligands increase splitting and may be low spin
D: CO, CN-, > phenanthroline > NO2
- > NCS-

7. CO, CN- > phen > en > NH3 > NCS- > H2O > F- > RCO2
- > OH- > Cl- > Br- > I-
Strong field,
 acceptors
large D
low spin
s only
Weak field,
 donors
small D
high spin

8. y
x
z
Most convenient to use a local coordinate
system on each ligand with
y pointing in towards the metal. py to be used
for s bonding.
z being perpendicular to the molecular plane. pz
to be used for  bonding perpendicular to the
plane, ^.
x lying in the molecular plane. px to be used
for  bonding in the molecular plane, |.

9. ML4 square planar complexes
ligand group orbitals and matching metal orbitals
s bonding
 bonding (in)
 bonding
(perp)

10. ML4 square planar complexes
MO diagram
s-only bonding Sample -
bonding
eg

11. An attempt to systematize the interactions for all geometries.
M
1
6
5
4
2
3
M
10
9
7
8
M 2
6
1
12
11
The various complexes may be fashioned out of the ligands
above
Linear: 1,6
Trigonal: 2,11,12
T-shape: 1,3,5
Tetrahedral: 7,8,9,10
Square planar: 2,3,4,5
Trigonal bipyramid: 1,2,6,11,12
Square pyramid: 1,2,3,4,5
Octahedral: 1,2,3,4,5,6

12. All s interactions with the ligands are stabilizing to the
ligands and destabilizing to the d orbitals. The interaction of a
ligand with a d orbital depends on their orientation with
respect to each other, estimated by their overlap which can be
calculated.
The total destabilization of a d orbital comes from all the
interactions with the set of ligands.
For any particular complex geometry we can obtain the
overlaps of a particular d orbital with all the various ligands
and thus the destabilization.

13. ligand dz2 dx2-y2
dxy dxz dyz
1 1 es 0 0 0 0
2 ¼ ¾ 0 0 0
3 ¼ ¾ 0 0 0
4 ¼ ¾ 0 0 0
5 ¼ ¾ 0 0 0
6 1 0 0 0 0
7 0 0 1/3 1/3 1/3
8 0 0 1/3 1/3 1/3
9 0 0 1/3 1/3 1/3
10 0 0 1/3 1/3 1/3
11 ¼ 3/16 9/16 0 0
12 1/4 3/16 9/16 0 0
Thus, for example a dx2-y2 orbital is destabilized by (3/4 +6/16) es
= 18/16 es in a trigonal bipyramid complex due to s interaction.
The dxy, equivalent by symmetry, is destabilized by the same
amount. The dz2 is destabililzed by 11/4 es.

14. Coordination Chemistry
Electronic Spectra of Metal Complexes

15. Electronic spectra (UV-vis spectroscopy)

16. Electronic spectra (UV-vis spectroscopy)
DE
hn

17. The colors of metal complexes

19. Electronic configurations of multi-electron atoms
What is a 2p2 configuration?
n = 2; l = 1; ml = -1, 0, +1; ms = ± 1/2
Many configurations fit that description
These configurations are called microstates
and they have different energies
because of inter-electronic repulsions

20. Electronic configurations of multi-electron atoms
Russell-Saunders (or LS) coupling
For each 2p electron
n = 1; l = 1
ml = -1, 0, +1
ms = ± 1/2
For the multi-electron atom
L = total orbital angular momentum quantum number
S = total spin angular momentum quantum number
Spin multiplicity = 2S+1
ML = ∑ml (-L,…0,…+L)
MS = ∑ms (S, S-1, …,0,…-S)
ML/MS define microstates and L/S define
states (collections of microstates)
Groups of microstates with the same
energy are called terms

21. Determining the microstates for p2

22. Spin multiplicity 2S + 1

23. Determining the values of L, ML, S, Ms for different terms
1S
1P

24. Classifying the microstates for p2
Spin multiplicity = # columns of microstates
Next largest ML is +1,
so L = 1 (a P term)
and MS = 0, ±1/2 for ML = +1,
2S +1 = 3
3P
One remaining microstate
ML is 0, L = 0 (an S term)
and MS = 0 for ML = 0,
2S +1 = 1
1S
Largest ML is +2,
so L = 2 (a D term)
and MS = 0 for ML = +2,
2S +1 = 1 (S = 0)
1D

25. Largest ML is +2,
so L = 2 (a D term)
and MS = 0 for ML = +2,
2S +1 = 1 (S = 0)
1D
Next largest ML is +1,
so L = 1 (a P term)
and MS = 0, ±1/2 for ML = +1,
2S +1 = 3
3P
ML is 0, L = 0
2S +1 = 1
1S

26. Energy of terms (Hund’s rules)
Lowest energy (ground term)
Highest spin multiplicity
3P term for p2 case
If two states have
the same maximum spin multiplicity
Ground term is that of highest L
3P has S = 1, L = 1

27. Determining the microstates for s1p1

28. Determining the terms for s1p1
Ground-state term

29. Coordination Chemistry
Electronic Spectra of Metal Complexes
cont.

30. Electronic configurations of multi-electron atoms
Russell-Saunders (or LS) coupling
For each 2p electron
n = 1; l = 1
ml = -1, 0, +1
ms = ± 1/2
For the multi-electron atom
L = total orbital angular momentum quantum number
S = total spin angular momentum quantum number
Spin multiplicity = 2S+1
ML = ∑ml (-L,…0,…+L)
MS = ∑ms (S, S-1, …,0,…-S)
ML/MS define microstates and L/S define
states (collections of microstates)
Groups of microstates with the same
energy are called terms

31. before we did:
p2
ML & MS
Microstate
Table
States (S, P, D)
Spin multiplicity
Terms
3P, 1D, 1S
Ground state term
3P

32. For metal complexes we need to consider
d1-d10
d2
3F, 3P, 1G, 1D, 1S
For 3 or more electrons, this is a long tedious process
But luckily this has been tabulated before…

33. Transitions between electronic terms will give rise to spectra

34. Selection rules
(determine intensities)
Laporte rule
g  g forbidden (that is, d-d forbidden)
but g  u allowed (that is, d-p allowed)
Spin rule
Transitions between states of different multiplicities forbidden
Transitions between states of same multiplicities allowed
These rules are relaxed by molecular vibrations, and spin-orbit coupling

35. Group theory analysis of term splitting

36. dn Free ion GS Oct. complex Tet complex
d0 1S t2g
0eg
0 e0t2
0
d1 2D t2g
1eg
0 e1t2
0
d2 3F t2g
2eg
0 e2t2
0
d3 4F t2g
3eg
0 e2t2
1
d4 5D t2g
3eg
1 e2t2
2
d5 6S t2g
3eg
2 e2t2
3
d6 5D t2g
4eg
2 e3t2
3
d7 4F t2g
5eg
2 e4t2
3
d8 3F t2g
6eg
2 e4t2
4
d9 2D t2g
6eg
3 e4t2
5
d10 1S t2g
6eg
4 e4t2
6
Holes: dn = d10-n and neglecting spin dn = d5+n; same
splitting but reversed energies because positive.
A t2 hole in d5,
reversed energies,
reversed again
relative to
octahedral since tet.
Holes in d5
and d10,
reversing
energies
relative to
d1
An e electron
superimposed
on a spherical
distribution
energies
reversed
because
tetrahedral
Expect oct d1 and d6 to behave same as tet d4 and d9
Expect oct d4 and d9 (holes), tet d1 and d6 to be reverse of oct d1

37. Energy
ligand field strength
d1  d6 d4  d9
Orgel diagram for d1, d4, d6, d9
0 D
D
D
d4, d9 tetrahedral
or T2
or E
T2g or
Eg or
d4, d9 octahedral
T2
E
d1, d6 tetrahedral
Eg
T2g
d1, d6 octahedral

38. F
P
Ligand field strength (Dq)
Energy
Orgel diagram for d2, d3, d7, d8 ions
d2, d7 tetrahedral d2, d7 octahedral
d3, d8 octahedral d3, d8 tetrahedral
0
A2 or A2g
T1 or T1g
T2 or T2g
A2 or A2g
T2 or T2g
T1 or T1g
T1 or T1g
T1 or T1g

39. d2
3F, 3P, 1G, 1D, 1S
Real complexes

40. Tanabe-Sugano diagrams

41. Electronic transitions and spectra

42. Other configurations
d1 d9
d3
d2 d8

43. d3
Other configurations
The limit between
high spin and low spin

44. Determining Do from spectra
d1
d9
One transition allowed of energy Do

45. Lowest energy transition = Do
mixing
mixing
Determining Do from spectra

46. Ground state is mixing
E (T1gA2g) - E (T1gT2g) = Do

47. The d5 case
All possible transitions forbidden
Very weak signals, faint color

48. Some examples of spectra

49. Charge transfer spectra
LMCT
MLCT
Ligand character
Metal character
Metal character
Ligand character
Much more intense bands