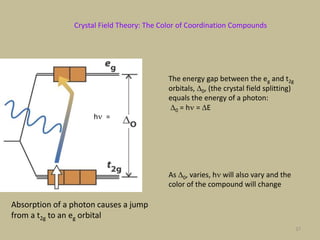
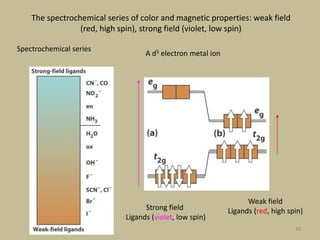
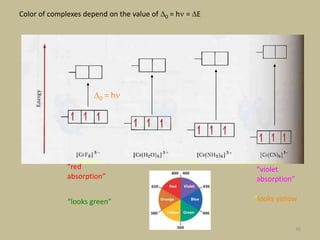
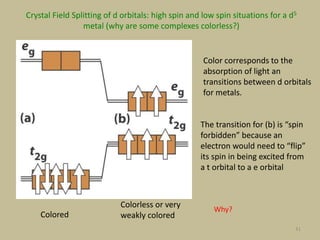
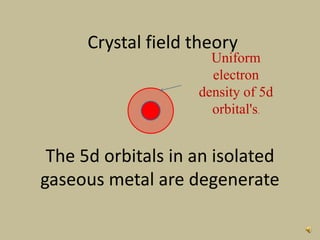
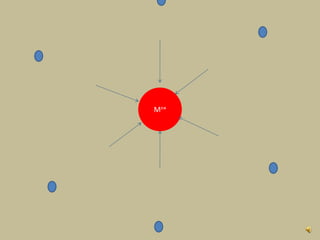
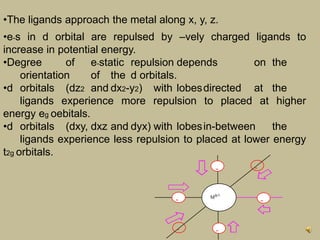
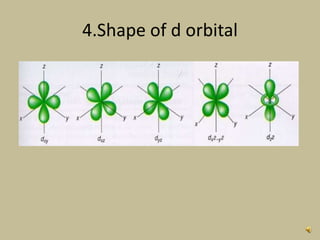
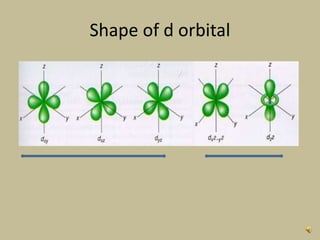
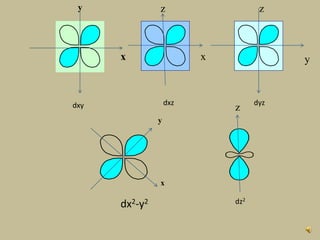
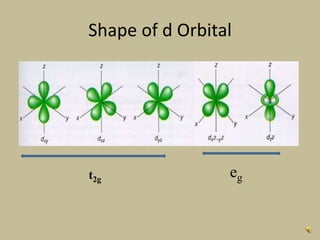
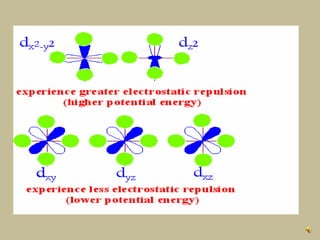
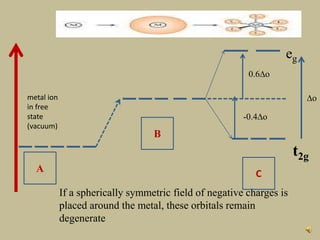
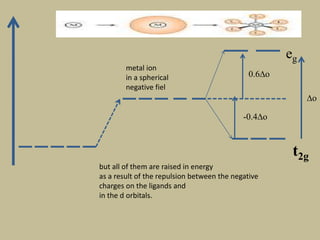
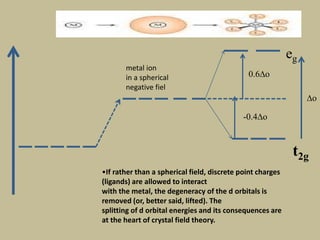
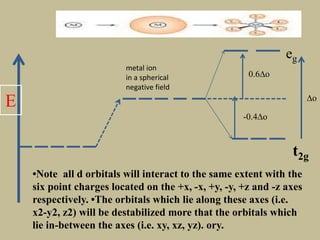
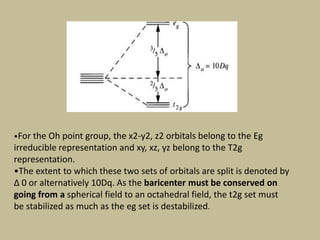
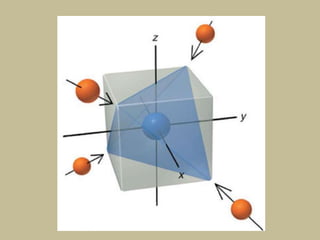
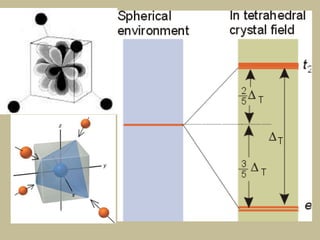
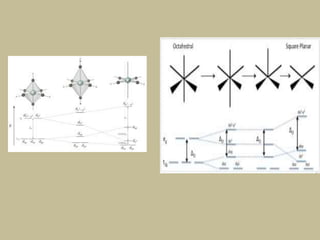
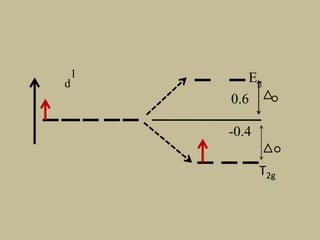
This document discusses crystal field theory (CFT), which interprets the chemistry of coordination compounds. Some key points: 1. CFT was proposed by Hans Bethe in 1929 and modified by J.H. Van Vleck in 1935 to allow for some covalency. It assumes electrostatic interactions between metal ions and ligands. 2. In an octahedral crystal field, the d-orbitals split into two sets - the lower energy t2g orbitals and higher energy eg orbitals. The splitting is called the crystal field splitting parameter Δo. 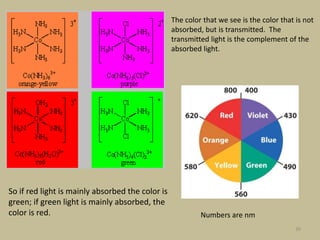3. The color of coordination compounds depends on the size of this splitting, as the energy difference corresponds to the absorption of photons.

1. Dr. S.H. Burungale
Crystal Field Theory

2. 1.Crystal Field Theory
This theory (CFT) largely replaced VB Theory for
interpreting the chemistry of coordination compounds.
•It was proposed by the physicist Hans Bethe in 1929.
•Subsequent modifications were proposed by J. H. Van
Vleck in 1935 to allow for some covalency in the
interactions. These modifications are often referred to as
Ligand Field Theory.

3. 2.CFT-Assumptions
•The interactions between the metal ion and the ligands are
purely electrostatic (ionic).
•The ligands are regarded as point charges
•If the ligand is negatively charged: ion-ion interaction. If
the ligand is neutral : ion-dipole interaction
•The electrons on the metal are under repulsive from those
on the ligands
•The electrons on metal occupy those d-orbitals farthest
away from the direction of approach of ligands

4. Mn+
3.Crystal Field Theory
Mn+
Free Mn+ ions

5. The 5d orbitals in an isolated
gaseous metal are degenerate
Mn+
Crystal field theory
Uniform
electron
density of 5d
orbital's.

7. Mn+

8. - -
- Mn+
-
- -
•The ligands approach the metal along x, y, z.
•e-s in d orbital are repulsed by –vely charged ligands to
increase in potential energy.
•Degree of e-static repulsion depends on the
orientation of the d orbitals.
•d orbitals (dz2 and dx2-y2) with lobesdirected at the
ligands experience more repulsion to placed at higher
energy eg oebitals.
•d orbitals (dxy, dxz and dyx) with lobesin-between the
ligands experience less repulsion to placed at lower energy
t2g orbitals.

9. 4.Shape of d orbital

10. Shape of d orbital

11. dxy
dx2-y2 dz2
dxz dyz
x
y
y
z
x
z
y
x
z

12. Shape of d Orbital
egt2g

14. 5.Crystal field Splitting in Octahedral Complexes
Crystal field splitting in octahedral complexe
is divided into three parts :
1. degenerate energy of d orbitals in
isolated or gaseous free metal ion .
2. Imaginary formation of Octahedral
complex
3. Actual Octahedral complex formation

15. eg
t2g
0.6∆o
∆o
-0.4∆o
If a spherically symmetric field of negative charges is
placed around the metal, these orbitals remain
degenerate
metal ion
in free
state
(vacuum)
A
B
C

16. eg
t2g
0.6∆o
∆o
-0.4∆o
but all of them are raised in energy
as a result of the repulsion between the negative
charges on the ligands and
in the d orbitals.
metal ion
in a spherical
negative fiel

17. eg
t2g
0.6∆o
∆o
-0.4∆o
•If rather than a spherical field, discrete point charges
(ligands) are allowed to interact
with the metal, the degeneracy of the d orbitals is
removed (or, better said, lifted). The
splitting of d orbital energies and its consequences are
at the heart of crystal field theory.
metal ion
in a spherical
negative fiel

18. eg
t2g
0.6∆o
∆o
-0.4∆o
•Note all d orbitals will interact to the same extent with the
six point charges located on the +x, -x, +y, -y, +z and -z axes
respectively. •The orbitals which lie along these axes (i.e.
x2-y2, z2) will be destabilized more that the orbitals which
lie in-between the axes (i.e. xy, xz, yz). ory.
metal ion
in a spherical
negative field
E

19. •For the Oh point group, the x2-y2, z2 orbitals belong to the Eg
irreducible representation and xy, xz, yz belong to the T2g
representation.
•The extent to which these two sets of orbitals are split is denoted by
Δ 0 or alternatively 10Dq. As the baricenter must be conserved on
going from a spherical field to an octahedral field, the t2g set must
be stabilized as much as the eg set is destabilized.

20. 6.In Tetrahedral Field

23. 7.Crystal field splitting In Squar
planar copmlexes
Larger crystal field splitting parameter
Squar Planar complexes
Octahedral is converted into squar
planar geometry

26. 8.Crystal Field Stabilization Energy
CFSE

27. Crystal Field Stabilization Energy
CFSE
d5
0.6
-0.4

30. 0.6
-0.4
T2g
Egd
1

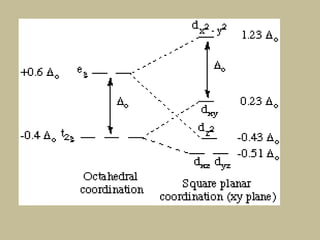
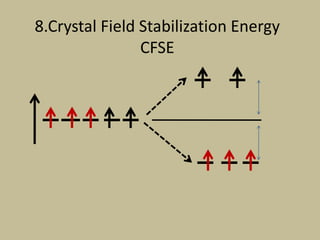
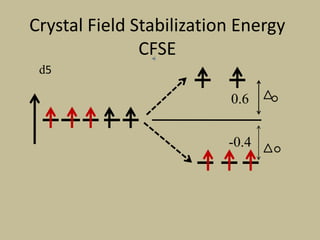
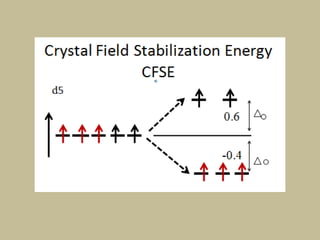
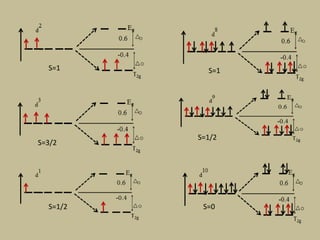
31. CFSE = [(0.6 x number of eg electrons)
- (0.4 x number of t2g electrons)]Δ
CFSE = [(0.6 x 0)
- (0.4 x 5)]Δo
=-2 Δo
CFSE = [(0.6 x 2)
- (0.4 x 3)]Δo
= 0Δo

32. 32
Crystal Field Splitting of d orbitals: high spin and
low spin situations for a d6 metal
Net unpaired
spins = 0:
Diamagnetic
Net unpaired
spins = 4:
Strongly paramagnetic
Low spin
Electrons spin
pair
High spin
Electrons do
Not spin pair
Ligand strength: (Weak) I- < F- < H2O < NH3 < CN- (Strong)
Large splitting
Small splitting

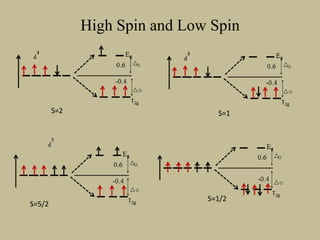
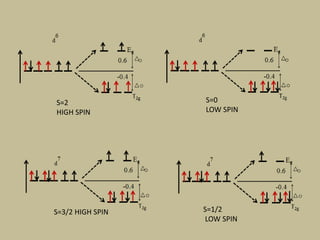
33. 33
Large splitting
Low spin
Small splitting
High spin
Energy gap larger than
advantage due to Hund’s rule
Energy gap small; Hund’s rule
applies
How many unpaired spins in Fe(CN)6
4- and in Fe(H2O)6
2+?
What is the charge of Fe in Fe(CN)6
4- and in Fe(H2O)6
2+?
Fe2+ in both cases Fe = [Ar]3d64s2; Fe2+ = [Ar]3d6
What kind of ligands are CN- and
H2O?
CN- is a strong field ligand and H2O
is a weak field ligand

34. High Spin and Low Spin
S=2 S=1
S=5/2
S=1/2

35. S=2
HIGH SPIN
S=0
LOW SPIN
S=3/2 HIGH SPIN S=1/2
LOW SPIN

36. S=1/2
S=1
S=3/2
S=1/2
S=0
S=1

37. 37
Crystal Field Theory: The Color of Coordination Compounds
h =
The energy gap between the eg and t2g
orbitals, 0, (the crystal field splitting)
equals the energy of a photon:
0 = h= E
As 0, varies, h will also vary and the
color of the compound will change
Absorption of a photon causes a jump
from a t2g to an eg orbital

38. 38
Strong field
Ligands (violet, low spin)
Weak field
Ligands (red, high spin)
The spectrochemical series of color and magnetic properties: weak field
(red, high spin), strong field (violet, low spin)
A d5 electron metal ion
Spectrochemical series

39. 39
The color that we see is the color that is not
absorbed, but is transmitted. The
transmitted light is the complement of the
absorbed light.
Numbers are nm
So if red light is mainly absorbed the color is
green; if green light is mainly absorbed, the
color is red.

40. 40
Color of complexes depend on the value of 0 = h= E
0 = h
“red
absorption”
“violet
absorption”
“looks green” “looks yellow

41. 41
Crystal Field Splitting of d orbitals: high spin and low spin situations for a d5
metal (why are some complexes colorless?)
Colored
Colorless or very
weakly colored
Why?
Color corresponds to the
absorption of light an
transitions between d orbitals
for metals.
The transition for (b) is “spin
forbidden” because an
electron would need to “flip”
its spin in being excited from
a t orbital to a e orbital

42. THANK YOU!!!!