Downloaded 95 times
Uploaded byDeepanshi Deepanshi
The Solid State For Class XII
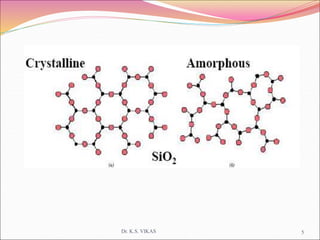
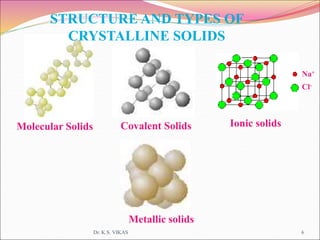
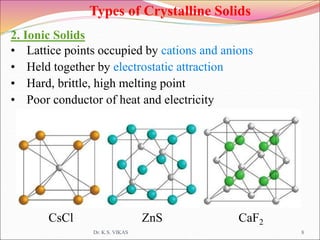
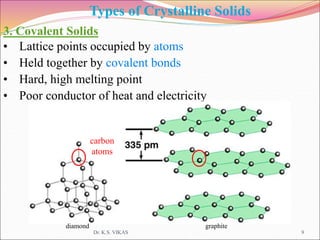
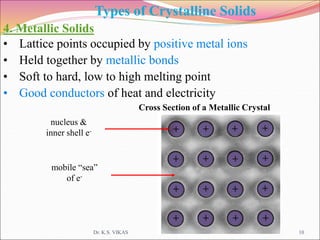
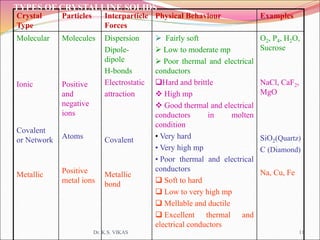
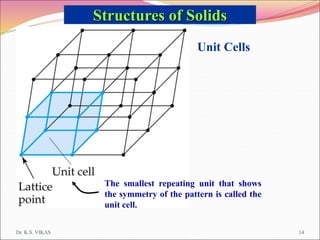
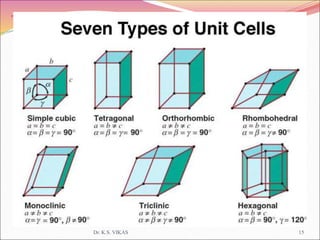
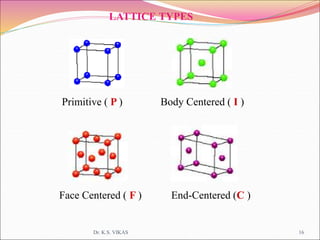
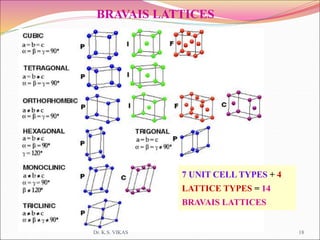
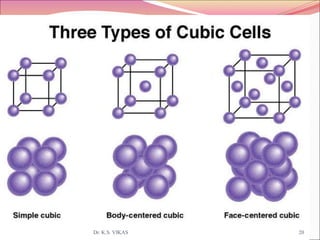
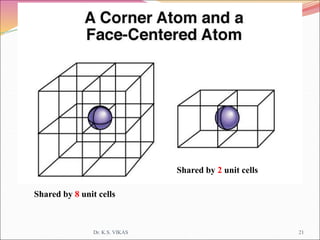
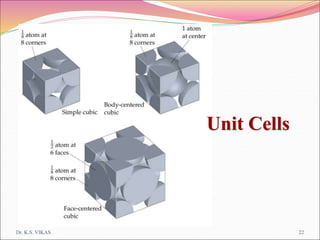
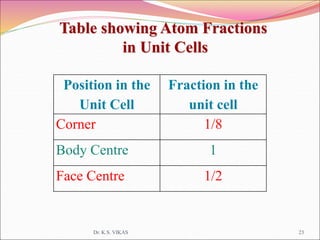
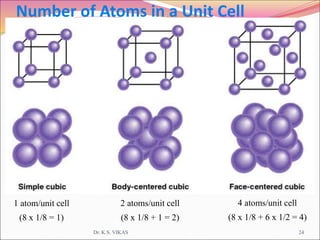
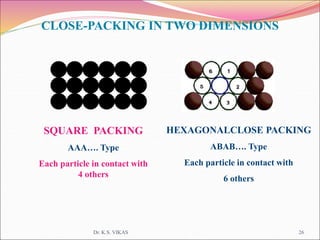
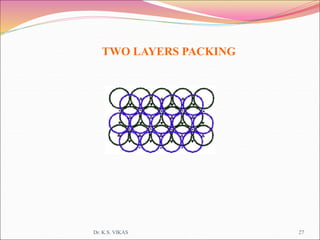
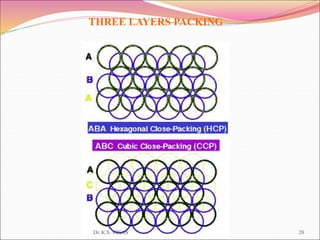
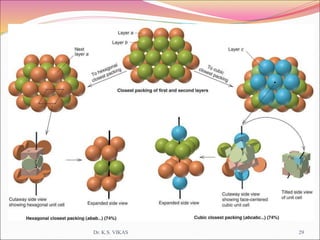
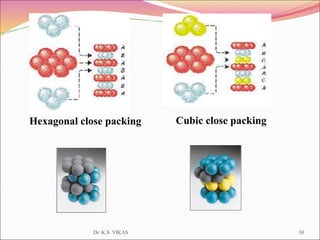
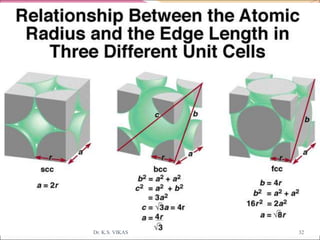
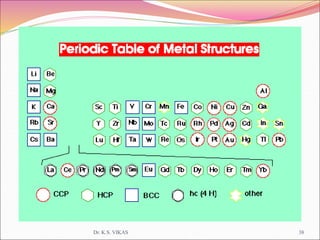
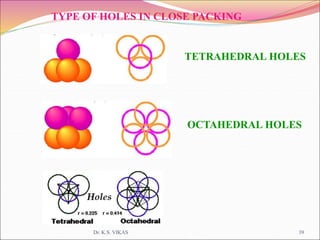
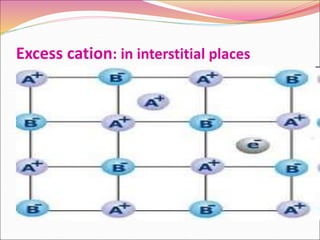
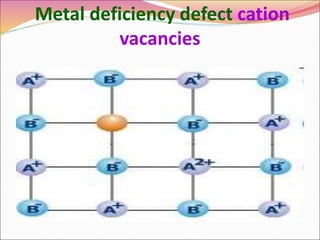
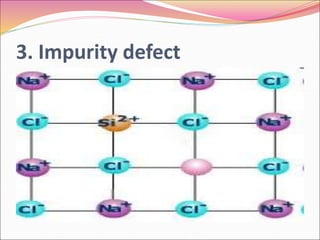
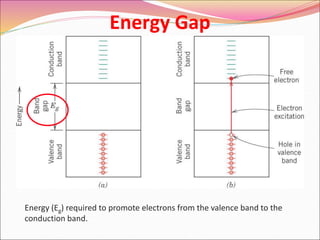
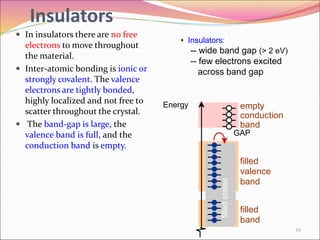
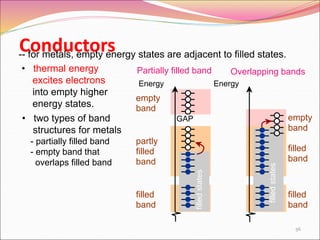
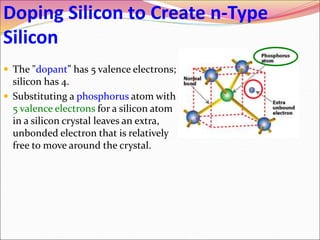
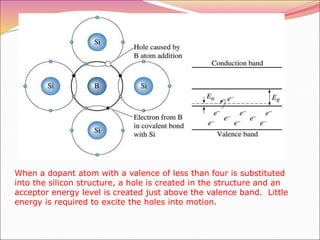
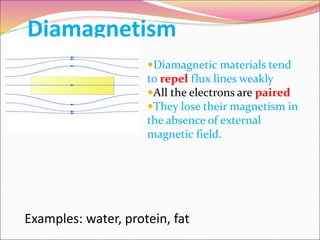
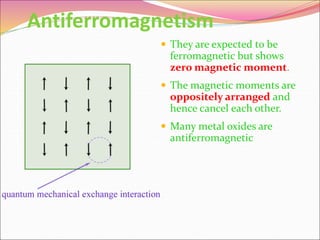
This document discusses different types of solids and their structures. It describes two main types of solids - crystalline and amorphous. Crystalline solids have long-range order while amorphous solids have short-range order. Crystalline solids are further divided into molecular, ionic, covalent and metallic solids based on the type of bonding between particles. The document also discusses crystal structures, unit cells, Bravais lattices and close packing of spheres. It covers defects in solids and electrical, magnetic and optical properties of materials.
More Related Content
Similar to The Solid State For Class XII
The Solid State For Class XII
- 1. THE SOLID STATE Dr.K.S. VIKAS 1
- 2. CONTENTS Types ofsolids Types of structures adopted by solids Imperfections in solids Dr. K.S. VIKAS 2
- 3. SOLIDS can bedivided into two categories. Crystalline Amorphous Crystalline has long range order Amorphous materials have short range order Dr. K.S. VIKAS 3
- 4. Dr. K.S. VIKAS •Crystalline solid: well-ordered, definite arrangements of molecules, atoms or ions. • Crystals have an ordered, repeated structure. • sharp melting point • Anisotropy • True solids • Amorphous solid: no definite arrangement of molecules, atoms, or ions (i.e., lack well-defined structures or shapes). • Amorphous solids vary in their melting points. • Isotropy • Pseudo solids (super cooled liquids) Types of Solids 4
- 5.
- 6. Molecular Solids CovalentSolids Ionic solids Metallic solids Na+ Cl- STRUCTURE AND TYPES OF CRYSTALLINE SOLIDS Dr. K.S. VIKAS 6
- 7. Types of CrystallineSolids 1. Molecular Solids • Lattice points occupied by molecules • Held together by intermolecular forces like London forces, dipole-dipole force or hydrogen bonding • Soft, low melting point • Poor conductor of heat and electricity Dr. K.S. VIKAS 7
- 8. Types of CrystallineSolids 2. Ionic Solids • Lattice points occupied by cations and anions • Held together by electrostatic attraction • Hard, brittle, high melting point • Poor conductor of heat and electricity CsCl ZnS CaF2 Dr. K.S. VIKAS 8
- 9. Types of CrystallineSolids 3. Covalent Solids • Lattice points occupied by atoms • Held together by covalent bonds • Hard, high melting point • Poor conductor of heat and electricity diamond graphite carbon atoms Dr. K.S. VIKAS 9
- 10. Types of CrystallineSolids 4. Metallic Solids • Lattice points occupied by positive metal ions • Held together by metallic bonds • Soft to hard, low to high melting point • Good conductors of heat and electricity Cross Section of a Metallic Crystal nucleus & inner shell e- mobile “sea” of e- Dr. K.S. VIKAS 10
- 11. Crystal Type Particles Interparticle Forces Physical BehaviourExamples Molecular Ionic Covalent or Network Metallic Molecules Positive and negative ions Atoms Positive metal ions Dispersion Dipole- dipole H-bonds Electrostatic attraction Covalent Metallic bond Fairly soft Low to moderate mp Poor thermal and electrical conductors Hard and brittle High mp Good thermal and electrical conductors in molten condition • Very hard • Very high mp • Poor thermal and electrical conductors Soft to hard Low to very high mp Mellable and ductile Excellent thermal and electrical conductors O2, P4, H2O, Sucrose NaCl, CaF2, MgO SiO2(Quartz) C (Diamond) Na, Cu, Fe TYPES OF CRYSTALLINE SOLIDS Dr. K.S. VIKAS 11
- 12. CRYSTAL STRUCTURE Cristal Lattice:Crystal Lattice is the arrangement of points in three dimensional space, representing constituent particles in a crystal. Space Lattice Arrangements of atoms = Lattice of points onto which the atoms are hung. Elemental solids (Argon): Basis = single atom. Polyatomic Elements: Basis = two or four atoms. Complex organic compounds: Basis = thousands of atoms. + Space Lattice + Basis = Crystal Structure = • • • • • • • • • Dr. K.S. VIKAS 12
- 13. Definitions 1. The unitcell “The smallest repeat unit of a crystal structure, which when repeats in all the three dimensions to form the crystal” The unit cell is a box with: • 3 sides - a, b, c • 3 angles - , , Dr. K.S. VIKAS 13
- 14. Dr. K.S. VIKAS UnitCells The smallest repeating unit that shows the symmetry of the pattern is called the unit cell. Structures of Solids 14
- 15. TWO DIMENTIONAL UNITCELL POSSIBILITIES OF NaCl Na+ Cl- Dr. K.S. VIKAS 15
- 16. Primitive ( P) Body Centered ( I ) Face Centered ( F ) End-Centered (C ) LATTICE TYPES Dr. K.S. VIKAS 16
- 17. Lattices In 1848,Auguste Bravais demonstrated that in a 3-dimensional system there are fourteen possible lattices A Bravais lattice is an infinite array of discrete points with identical environment seven crystal systems + four lattice centering types = 14 Bravais lattices Auguste Bravais (1811-1863) Dr. K.S. VIKAS 17
- 18. BRAVAIS LATTICES 7 UNITCELL TYPES + 4 LATTICE TYPES = 14 BRAVAIS LATTICES Dr. K.S. VIKAS 18
- 19. Dr. K.S. VIKAS •Three common types of Cubic unit cell. • Primitive cubic, atoms at the corners of a simple cube – each atom shared by 8 unit cells; Common Types of Cubic Unit Cells 19 • Body-centered cubic (bcc), atoms at the corners of a cube plus one in the center of the body of the cube, – corner atoms shared by 8 unit cells, center atom completely enclosed in one unit cell; • Face-centered cubic (fcc), atoms at the corners of a cube plus one atom in the center of each face of the cube, – corner atoms shared by 8 unit cells, face atoms shared by 2 unit cells.
- 20.
- 21. Shared by 8unit cells Shared by 2 unit cells Dr. K.S. VIKAS 21
- 22. Dr. K.S. VIKAS UnitCells 22
- 23. Dr. K.S. VIKAS23 Table showing Atom Fractions in Unit Cells Position in the Unit Cell Fraction in the unit cell Corner 1/8 Body Centre 1 Face Centre 1/2
- 24. 1 atom/unit cell (8x 1/8 = 1) 2 atoms/unit cell (8 x 1/8 + 1 = 2) 4 atoms/unit cell (8 x 1/8 + 6 x 1/2 = 4) Number of Atoms in a Unit Cell Dr. K.S. VIKAS 24
- 25. CLOSE-PACKING OF SPHERES Dr.K.S. VIKAS 25
- 26. CLOSE-PACKING IN TWODIMENSIONS SQUARE PACKING AAA…. Type Each particle in contact with 4 others HEXAGONALCLOSE PACKING ABAB…. Type Each particle in contact with 6 others Dr. K.S. VIKAS 26
- 27. TWO LAYERS PACKING Dr.K.S. VIKAS 27
- 28. THREE LAYERS PACKING Dr.K.S. VIKAS 28
- 29.
- 30. Hexagonal close packingCubic close packing Dr. K.S. VIKAS 30
- 31. Packing Efficiency volume ofsphere Packing Efficiency =---------------------------- X 100 Total volume of cube Dr. K.S. VIKAS 31 (N)x (4/3 Π r3) = --------------------- X100 a3
- 32.
- 33. Packing Efficiency ofPrimitive Cubic Crystal volume of sphere Packing Efficiency =---------------------------- X 100 Total volume of cube Dr. K.S. VIKAS 33 (N)x (4/3 Π r3) = --------------------- X100 a3 1 x (4/3 Π r3) = --------------------- X100 (2r)3 = 52.4%
- 34. Packing Efficiency ofBody Centred Cubic Crystal volume of sphere Packing Efficiency =---------------------------- X 100 Total volume of cube Dr. K.S. VIKAS 34 (N)x (4/3 Π r3) = --------------------- X100 a3 2 x (4/3 Π r3) = --------------------- X100 (4/3 r)3 = 68%
- 35. Packing Efficiency ofbcc, hcp & ccp volume of sphere Packing Efficiency =---------------------------- X 100 Total volume of cube Dr. K.S. VIKAS 35 (N)x (4/3 Π r3) = --------------------- X100 a3 4 x (4/3 Π r3) = --------------------- X100 (2√2 r)3 = 74%
- 36. NON-CLOSE-PACKED STRUCTURES 68% ofspace is occupied Coordination number = 8 a) Body centered cubic ( BCC ) b) Primitive cubic ( P) 52% of space is occupied Coordination number = 6 Dr. K.S. VIKAS 36
- 37. Dr. K.S. VIKAS Face-CenteredCubic Crystal Structure 68% of space is occupied Hexagonal close packing & Cubic close packing also occupy the same space
- 38.
- 39. TETRAHEDRAL HOLES OCTAHEDRAL HOLES TYPEOF HOLES IN CLOSE PACKING Dr. K.S. VIKAS 39
- 40.
- 41. Crystal Defects • Perfectcrystals do not exist; even the best crystals have defects. – defects are imperfections in the regular repeating pattern – Point defect – Line defect 1. Point Defects A.Vacancies – given a perfect crystal (e.g. of Cu), an atom can be placed on the outside of the cell to produce a vacancy (≡ □). Dr. K.S. VIKAS 41
- 42. Types of Defects StoichiometricDefects: stoichiometry is not disturbed Non-stoichiometric Defects: stoichiometry is disturbed Impurity defects
- 43. Stoichiometric Defects Schottky defect Frenkeldefect Non-stoichiometric Defects Metal excess defect Metal deficiency defect
- 44. 1. Stoichiometric Defects 1)Shottky Defect – equal numbers of anion and cation vacancies. – may be randomly distributed, but tend to cluster because of oppositely charged vacancies. – most important with alkali halides. Dr. K.S. VIKAS 44
- 45. 2) Frenkel Defect Dislocationof cation cation occupies interstitial position (void between normal atomic position). Dr. K.S. VIKAS 45
- 46. Non-stoichiometric Defects Metal excessdefect anion vacancies excess cation Metal deficiency defect cation vacancies
- 47. Metal excess defect Anion vacancies Ananion is missing from the crystal lattice and that place is occupied by an electron Color Centers (F-center; Ger: farbenzentre) Dr. K.S. VIKAS 47
- 48. Excess cation: ininterstitial places
- 49. Metal deficiency defectcation vacancies
- 50.
- 51.
- 52.
- 53. Energy (Eg) requiredto promote electrons from the valence band to the conduction band. Energy Gap
- 54. Insulators In insulatorsthere are no free electrons to move throughout the material. Inter-atomic bonding is ionic or strongly covalent. The valence electrons are tightly bonded, highly localized and not free to scatter throughout the crystal. The band-gap is large, the valence band is full, and the conduction band is empty. 54 • Insulators: -- wide band gap (> 2 eV) -- few electrons excited across band gap Energy filled band filled valence band filled states GAP empty band conduction
- 55. 55 Semiconductors • Semiconductors: -- narrowband gap (< 2 eV) -- more electrons excited across band gap Energy filled band filled valence band filled states GAP ? empty band conduction In semiconductors, bonding is predominantly covalent (relatively weak). These electrons are more easily removed by thermal excitation. The band-gap is smaller, the valence band is full, and the conduction band is empty.
- 56. 56 Conductors -- for metals,empty energy states are adjacent to filled states. • two types of band structures for metals • thermal energy excites electrons into empty higher energy states. - partially filled band - empty band that overlaps filled band filled band Energy partly filled band empty band GAP filled states Partially filled band Energy filled band filled band empty band filled states Overlapping bands
- 57.
- 58. Intrinsic Semiconductor materials Siliconand germanium each have 4 electrons in their outer orbital. This allows them to form crystals. In a silicon lattice, all silicon atoms covalently bond to 4 neighbors, leaving no free electrons to conduct electric current. This makes a silicon crystal an insulator rather than a conductor. A chip, an LED and a transistor are all made from semiconductor material.
- 59. Intrinsic Semiconductor Onheating some of the covalent bonds between silicon atoms are broken and as a result they conduct electricity Semiconductors in the pure form is called intrinsic semiconductors
- 60. Extrinsic semiconductors Theycontain some suitable impurities in their crystal lattice. This process of adding impurities to the crystal is called doping . They are classified into two based on the impurity present in it. n-type semiconductor p-type semiconductor
- 61. Doping Silicon toCreate n-Type Silicon The "dopant” has 5 valence electrons; silicon has 4. Substituting a phosphorus atom with 5 valence electrons for a silicon atom in a silicon crystal leaves an extra, unbonded electron that is relatively free to move around the crystal.
- 62. Doping Silicon toCreate p-Type Silicon The "dopant” has 5 valence electrons; silicon has 4. Substituting a boron atom with 3 valence electrons for a silicon atom in a silicon crystal leaves a hole (a bond missing an electron) that is relatively free to move around the crystal.
- 63. When a dopantatom with a valence of less than four is substituted into the silicon structure, a hole is created in the structure and an acceptor energy level is created just above the valence band. Little energy is required to excite the holes into motion.
- 64.
- 65. Diamagnetism Diamagnetic materials tend torepel flux lines weakly All the electrons are paired They lose their magnetism in the absence of external magnetic field. Examples: water, protein, fat
- 66. Paramagnetism Paramagnetic substancesare attracted weakly by a magnetic field. They lose their magnetism in the absence of external magnetic field. They have one or more unpaired electrons. E.g. O2, Cu2+, Fe3+, Cr3+
- 67. Ferromagnetism Materials thatretain a magnetization in zero field They are attracted strongly by a magnetic field They have more unpaired electrons. Examples: iron, cobalt
- 68. Antiferromagnetism They areexpected to be ferromagnetic but shows zero magnetic moment. The magnetic moments are oppositely arranged and hence cancel each other. Many metal oxides are antiferromagnetic
- 69. Ferrimagnetism They areexpected to be ferromagnetic but shows only small magnetic moment. The magnetic moments are oppositely arranged but all magnetic moments are not canceled. E.g. Fe2O3