Presentasi ini membahas sistem koordinat kutub, termasuk definisi, persamaan, hubungannya dengan koordinat Cartesius, grafik persamaan kutub, perpotongan kurva, kalkulus dan luas dengan koordinat kutub, serta garis singgung dalam koordinat kutub. Presentasi ini disampaikan oleh Kelompok 9 Jurusan Matematika Fakultas MIPA Universitas Negeri Manado.

1. Presentasi
Kelompok 9
Koordinat Kutub
Jurusan Matematika
Fakultas MIPA
Universitas Negeri Manado

2. A. System koordinat kutub
Dua orang Perancis yaitu Pierre Fermat dan Rene Descartes, telah
memperkenalkan system koordinat yang sekarang kita kenal dengan
sebutan system koordinat Cartesius atau siku- siku. Dasar pemikiran
mereka ialah untuk menunjukkan kedudukan titik P pada bidang
dengan dua bilangan yang ditulis dengan lambang (x,y) setiap bilangan
menggambarkan jarak berarah dari dua sumbu yang tegak lurus
sesamanya

3. B. Koordinat Kutub
Setiap titik P (selain dari kutub) adalah perpotongan antara
sebuah lingkaran tunggal yang berpusat di 0 dan sebuah sinar
tunggal yang memancar dari 0. Jika r adalah jari- jari
lingkaran dan θ adalah salah satu sudut antara sinar dan
sumbu kutub, maka (r, θ) dinamakan sepasang koordinat kutub
dari titik P

4. C. Persamaan Kutub
Contoh persamaan kutub adalah:
Grafik persamaan kutub adalah himpunan titik-titik yang
mempunyai paling sedikit sepasang koordinat kutub yang
memenuhi persamaan yang bersangkutan.

5. D. Hubungan dengan Koordinat Cartesius
Andaikan sumbu kutub berimpit dengan sumbu x positif
system koordinat Cartesius. Maka koordinat kutub (r, θ)
sebuah titik P dan koordinat Cartesius (x, y) titik itu
dihubungkan oleh persamaan :

6. E. Persamaan Kutub untuk Garis, Lingkaran dan Konik
GARIS : Apabila P (r, θ) sebuah titik pada garis, maka ;
cos (θ - θ , atau 0) =
LINGKARAN : Apabila pusatnya di (r 0, θ0), persamaannya agak
rumit, kecuali kalau kita pilih r0 = a (Gambar 7.10). Maka menurut
hukum kosinus, a2 = r2 + a2 – 2ra cos (θ - θ0) yang dapat
disederhanakan menjadi : Lingkaran : r = 2a cos (θ - θ0)
KONIK : definisi konik, yaitu PF =e PL kita akan memperoleh
Atau secara setara : konik :

7. GAMBAR

8. F. Grafik Persamaan Kutub
 Kardiot
Limason
Mawar
Spiral
Sifat simetri dapat membantu kita menggambar sebuah grafik.
1. Grafik persamaan kutub simetri terhadap sumbu y (yaitu garis θ = π/2) apabila
θ diganti dengan π-θ menghasilkan persamaan yang sama (Gambar 7.14).
2. Grafik persamaan kutub simetri terhadap sumbu x (yaitu sumbu kutub dan
perpanjangannya ke kiri) apabila θ diganti dengan –θ menghasilkan persamaan
yang sama (Gambar 7.13).
3. Grafik persamaan kutub simetri terhadap titik asal, apabila r diganti –r
menghasilkan persamaan yang sama (Gambar 7.15).

9. G. Perpotongan Kurva-kurva Dengan Koordinat Kutub
Untuk dapat memperoleh semua perpotongan dua kurva
dengan koordinat kutub, selesaikanlah persamaan-persamaan
bersama-sama; kemudian gambarlah grafiknya secara seksama
untuk memperoleh titik potong lain yang masih mungkin.

10. H. Kalkulus Dengan Koordinat Kutub
Dengan koordinat Cartesius, unsure luas dasar adalah luas persegi
panjang. Dengan koordinat kutub unsure luas dasar ini adalah luas
suatu juring (sektor) lingkaran (Gambar 7.23). Oleh karena luas
lingkaran dengan jari-jari r adalah πr2 , kita dapat menarik
kesimpulan bahwa luas sektor lingkaran dengan sudut pusat θ
radian adalah (θ/2π)πr2 . Sehingga :

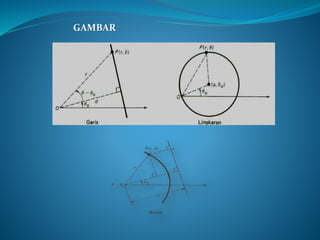
11. I. Luas dalam Koordinat Kutub
Andaikan r = f(θ) menentukan sebuah kurva pada bidang dengan f kontinu
dan tak negatif untuk α ≤ θ ≤ β dan β-α ≤ 2π. Maka kurva r = f(θ), θ = α’ dan
θ = β membatasi sebuah daerah R (Gambar 7.24 kiri); kita hendak menentukan
luas A(R). Kita bagi selang [α, β] menjadi n bagian selang oleh bilangan-bilangan
θi, I = 0, 1, 2, …n dengan α = θ0 < θ1 < θ2 < …< θn = β dengan demikian daerah R
terbagi menjadi daerah yang lebih kecil, yaitu R1, R2,…, Rn (Gambar 7.24
kanan). Maka A(R) = A(R1) + A(R2) + … + A(Rn).
Kita aproksimasi luas A(Ri) dengan dua jalan. Pada selang ke-I,[θi-1 , θi ],
f mencapai nilai minimum di ui dan mencapai nilai maksimumnya di vi (Gambar
4.25). Jadi, apabila Δθi = θi - θi-1, kita peroleh

12. J. Garis Singgung dalam Koordinat Kutub
Dengan koordinat Cartesius, kemiringan (slope) m dari garis singgung pada
sebuah kurva adalah m = dy/dx. Dengan koordinat kutub kemiringan ini
bukanlah dr/dθ. Apabila r = f(θ) menentukan persamaan kurva, kita tulis
Rumus di atas menjadi sederhana apabila grafik r = f(θ) melalui kutub.
Andaikan, sebagai contoh, untuk suatu sudut α, r = f(α) = 0 dan f’(α) ≠ 0.
Maka di kutub tersebut kita peroleh
Oleh karena garis θ = α memiliki kemiringan tan α juga, maka kita dapat
mengatakan bahwa garis tersebut menyinggung kurva di kutub.Jadi dapat
ditarik kesimpulan bahwa garis singgung kurva di kutub dapat ditemukan
dengan menyelesaikan persamaan f(θ) = 0.

13. Nama-Nama Kelompok
ROY S. MAHAJANI (13 531 115)
KEVIN TOLOLIU (13 531 049)