Dokumen ini membahas dua sistem koordinat yaitu koordinat kartesius dan koordinat kutub. Koordinat kartesius menggunakan dua bilangan x dan y untuk menentukan suatu titik. Sedangkan koordinat kutub menggunakan jarak r dari titik ke pusat dan sudut θ. Dokumen ini juga menjelaskan rumus untuk mengkonversi antara kedua sistem koordinat tersebut.

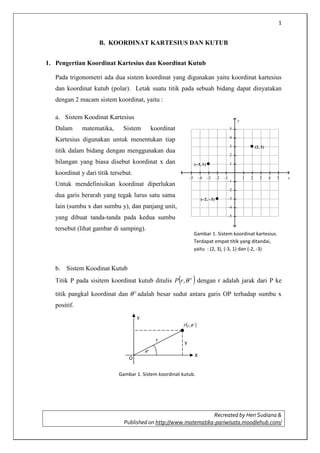
1. 1
B. KOORDINAT KARTESIUS DAN KUTUB
1. Pengertian Koordinat Kartesius dan Koordinat Kutub
Pada trigonometri ada dua sistem koordinat yang digunakan yaitu koordinat kartesius
dan koordinat kutub (polar). Letak suatu titik pada sebuah bidang dapat dinyatakan
dengan 2 macam sistem koordinat, yaitu :
a. Sistem Koodinat Kartesius
Dalam
matematika,
y
Sistem
koordinat
5
Kartesius digunakan untuk menentukan tiap
4
3
titik dalam bidang dengan menggunakan dua
(2, 3)
2
bilangan yang biasa disebut koordinat x dan
1
(–3, 1)
koordinat y dari titik tersebut.
–5
–4
–3
Untuk mendefinisikan koordinat diperlukan
–2
–1
–1
1
2
3
4
5
–2
dua garis berarah yang tegak lurus satu sama
(–2, –3)
–3
lain (sumbu x dan sumbu y), dan panjang unit,
–4
yang dibuat tanda-tanda pada kedua sumbu
–5
tersebut (lihat gambar di samping).
Gambar 1. Sistem koordinat kartesius.
Terdapat empat titik yang ditandai,
yaitu : (2, 3), (-3, 1) dan (-2, -3).
b. Sistem Koodinat Kutub
(
)
Titik P pada sisitem koordinat kutub ditulis P r , θ o dengan r adalah jarak dari P ke
titik pangkal koordinat dan θ o adalah besar sudut antara garis OP terhadap sumbu x
positif.
Y
(
P r ,θ o
r
θo
O
)
y
X
Gambar 1. Sistem koordinat kutub.
Recreated by Heri Sudiana &
Published on http://www.matematika-pariwisata.moodlehub.com/
x

2. 2
2. Mengkonversi Koordinat Kartesius ke Koordinat Kutub atau Sebaliknya
•
Jika pada koordinat kartesius titik P( x, y ) diketahui, maka koordinat kutub
(
)
P r , θ o dapat ditentukan dengan menggunakan rumus sebagai berikut :
r = x2 + y2
tan θ o =
•
y
y
⇔ θ o = arctan
x
x
(
Jika pada koordinat kutub titik P r , θ o
)
diketahui, maka koordinat kartesius titik
P( x, y ) dapat ditentukan dengan menggunakan rumus sebagai berikut :
y
⇔ y = r. sin θ o
r
x
cos θ o = ⇔ x = r. cos θ o
r
sin θ o =
Contoh Soal 1
(
)
Diketahui koordinat kutub titik P 4,60 o . Tentukan koordinat kartesius titik P.
Jawab :
(
)
Diketahui P 4,60 o , diperoleh r = 4 dan θ o = 60 o , maka
x = r. cos θ o
y = r. sin θ o
x = 4. cos 60 o
y = 4. sin 60 o
x = 4. 1
2
y = 4. 1 3
2
x=2
y=2 3
(
(
)
Jadi, koordinat kartesius dari titik P 4,60 o adalah titik P 2,2 3
Contoh Soal 2
(
)
)
Diketahui koordinat kartesius titik P − 2,−2 3 . Tentukan koordinat kutub dari titik P.
Recreated by Heri Sudiana &
Published on http://www.matematika-pariwisata.moodlehub.com/

3. 3
Jawab :
(
)
Diketahui P − 2,−2 3 , diperoleh x = −2 dan y = −2 3 yang terletak di kuadran III
( mengapa ? ).
tan θ o =
r = x2 + y2
r=
r=
(− 2)2 + (− 2
4 + (4.3)
3
)
2
y
−2
=
= 3
x −2 3
⇔ θ o = arctan 3
⇔ θ o = 240 o (kuadranIII )
r = 16
r=4
(
)
(
)
Jadi, koordinat kutub dari titik P − 2,−2 3 adalah titik P 4,240 o .
Recreated by Heri Sudiana &
Published on http://www.matematika-pariwisata.moodlehub.com/