This document discusses vertical curves used in transportation design. Vertical curves provide a smooth transition between different road or rail grades. They are designed using parabolic equations to maintain a constant rate of change in slope. The key points are: - Vertical curves connect two different grades using a parabolic shape. - Their design ensures a constant rate of change in slope for driver comfort. - The general parabolic equation and methods for computing curve elements like high/low points and elevations at different points are presented.

1. 1
Vertical Curves
20/01/2013

2. Vertical curves are the curves used in a vertical plane to provide a
smooth transition between the grade lines of highways and railroads.
PVI
2
g1
BVC
g2
EVC
L
0 + 00
Forward Stations
20/01/2013

3. In previous Figure;
• g1 is the slope of the lower chainage grade line.
• g2 is the slope of the higher chainage grade line.
• BVC is the beginning of the vertical curve.
• EVC is the end of the vertical curve. 3
• PVI is the point of intersection of the two adjacent gradelines.
• L is the length of vertical curve.
• A = g2 – g1, is the algebraic change in slope direction.
20/01/2013

4. General Equation of Parabola
The vertical axis parabola is used in vertical alignment design. The
parabola has two desirable characteristics such as;
• A constant rate of change of slope.
4
• Ease of computation of vertical offsets.
y  a x2  b x  c
The slope :
dy
 2a x  b
dx
The rate of change of slope :
d2y
 2a (const.)
dx
A
 2a
L
20/01/2013

5. General Equations of Parabola
Y
Y
PVI
EVC
EVC
X X
BVC X BVC X
PVI 5
b) Crest curve
a) Sag curve
Y Y
If the origin of the axes is placed at BVC, the general equation becomes;
y  a x2  b x
y  a x 2  g1 x
The slope at the origin is g1 :
dy
 slope  2 a x  g1
dx
20/01/2013

6. L
L/2 L/2
E
V
x
ax2
g1x
6
m
BVC
C E
EVC
Crest Curve
Geometric Properties of the Parabola
20/01/2013

7. Geometric Properties of the Parabola
From previous Figure;
• g1x is the difference in elevation between the BVC and a point on the g1
gradeline at a distance x.
7
• ax2 is the tangent offset between the gradeline and the curve.
• BVC + g1x – ax2 = curve elevation at distance x from the BVC.
• BVC to V = L/2 = V to EVC
• Offsets from the two gradelines are symmetrical with respect to the PVI (V).
• Cm = mV
20/01/2013

8. Computation of the High/Low Point on a Vertical Curve
Low Point
EVC
BVC
8
Tangent Through Low Point
PVI Slope = 2 ax + g1 = 0
The tangent drawn through the low point is horizontal with a slope of zero;
2 ax + g1 = 0
x = - g1 (L/A)
Where x is the distance from the BVC to the high or low point.
20/01/2013

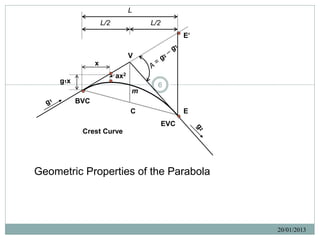
9. Computing a Vertical Curve
Procedures for computing a vertical curve:
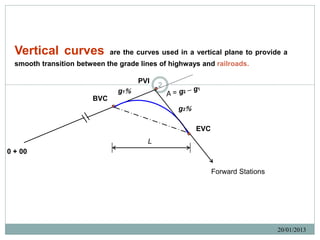
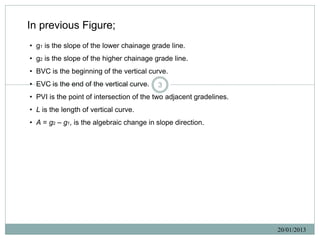
1. Compute the algebraic difference in grades A = g1 – g2.
2. Compute the stationing of BVC and EVC. Subtract/add L/2 to the PVI.
3. Compute the distance from the BVC to the high or low point; x = - g1(L/A). Determine
the station of the high or low point. 9
4. Compute the tangent gradeline elevation of the BVC and the EVC.
5. Compute the tangent gradeline elevation for each required station.
6. Compute the midpoint of the chord elevation: [(elevation of BVC + elevation of EVC)/2].
7. Compute the tangent offset d at PVI, Vm, d = (difference in elevation of PVI and C)/2).
8. Compute the tangent offset for each individual station (see line ax2),
tangent offset = d (x)2/(L/2)2 = (4d) x2/L2 where x is the distance from the BVC or EVC
(whichever is closer) to the required station.
9. Compute the elevation on the curve at each required station by combining the tangent
offsets with the appropriate tangent gradeline elevations. Add for sag curves and
subtract for crest curves.
20/01/2013

10. Problem: You are given the following information: L = 300 ft, g1 = - 3.2%, g2 = + 1.8%,
PVI at 30 + 30 with elevation = 465.92. Determine the location of the low point and the
elevations on the curve at even stations, as well as the low point.
L = 300 ft
L/2 = 150 ft
1.875 469.67 10
BVC 467.795 EVC
28 + 80.00 31 + 80.00
470.72 468.62
d = 1.875 PVI
30 + 30.00 Low Point
465.92
Solution:
1. A = g2 – g1 = 1.8 – (- 3.2) = 5.0
2. Station BVC = PVI – L/2 = (30 + 30.00) – (1 + 50) = 28 + 80.00
Station EVC = PVI + L/2 = (30 + 30.00) + (1 + 50) = 31 + 80.0Ukkk
Check EVC – BVC = L; (31 + 80.00) – (28 + 80.00) = 300
20/01/2013

11. Solution:
3. Location of the low point; x = - g1L/A = (3.2  300)/5 = 192.00 ft from BVC.
4. Elevation BVC = Elevation PVI + (150 ft at 3.2%) = 465.92 + 4.80 = 470.72
Elevation EVC = Elevation PVI + (150 ft at 1.8%) = 465.92 + 2.70 = 468.62
5. Tangent gradeline elevations are computed and entered in the table below: e.g.
Elevation at 29 + 00 = 470.72 – (0.032  20) = 470.72 – 0.64 = 470.08
11
Station Tangent Elevations + Tangent Offset (x/L/2)2 .d = Curve Elevation
BVC 28 + 80 470.72 (0/150)2  1.875 = 0 470.72
29 + 00 470.08 (20/150)2  1.875 = 0.03 470.11
30 + 00 466.88 (120/150)2  1.875 = 1.20 468.08
PVI 30 + 30 465.92 (150/150)2  1.875 = 1.875 467.80
Low 30 + 72 466.68 (108/150)2  1.875 = 0.97 467.65
31 + 00 467.18 (80/150)2  1.875 = 0.53 467.71
EVC 31 + 80 468.62 (0/150)2  1.875 = 0 468.62
30 + 62 466.50 (118/150)2  1.875 = 1.16 467.66
30 + 72 466.68 (108/150)2  1.875 = 0.97 467.65
30 + 82 466.86 (98/150)2  1.875 = 0.80 467.66
20/01/2013

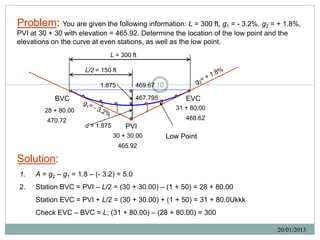
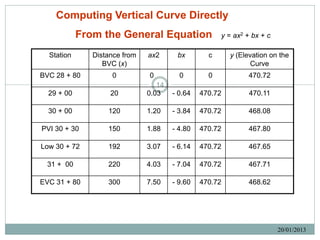
12. Solution:
6. Mid-chord elevation; [470.72 (BVC) + 468.62 (EVC)]/2 = 469.67 ft.
7. Tangent offset at PVI (d): d = (difference in elevation of PVI and mid-chord)/2
d = (469.67 – 465.92)/2 = 1.875 ft.
8. For other stations, tangent offsets are computed by multiplying the distance ratio
squared (x/L/2)2 by the maximum tangent offset (d). Refer to previous Table.
9. 12
The computed tangent offsets are added to the tangent elevation to determine the
curve elevation.
20/01/2013

13. Computing Vertical Curve Directly
From the General Equation
y = ax2 + bx + c
Where;
a = (g2 – g1)/2L 13
L, horizontal length of vertical curve.
c, elevation at BVC.
x, horizontal distance from BVC
y, elevation on the curve at distance x from the BVC.
Using previous given data, compute the vertical curve elevations
directly from parabolic general equation; y = ax2 + bx + c.
20/01/2013

14. Computing Vertical Curve Directly
From the General Equation y = ax2 + bx + c
Station Distance from ax2 bx c y (Elevation on the
BVC (x) Curve
BVC 28 + 80 0 0 0 0 470.72
14
29 + 00 20 0.03 - 0.64 470.72 470.11
30 + 00 120 1.20 - 3.84 470.72 468.08
PVI 30 + 30 150 1.88 - 4.80 470.72 467.80
Low 30 + 72 192 3.07 - 6.14 470.72 467.65
31 + 00 220 4.03 - 7.04 470.72 467.71
EVC 31 + 80 300 7.50 - 9.60 470.72 468.62
20/01/2013