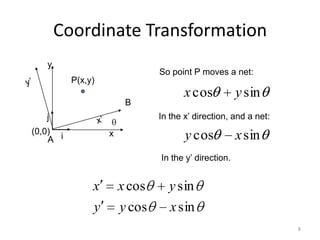
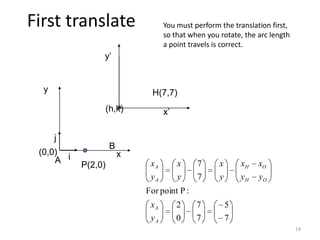
This document discusses coordinate transformations, including translating and rotating coordinate frames. It provides examples of how to calculate the coordinates of a point in a new frame after a translation or rotation from the original frame. Specifically, it shows how to calculate the new coordinates of point P if the original frame is translated to a new origin or rotated by 30 degrees. The key steps are to first translate the frame if needed, then apply the rotation matrix to calculate the new x' and y' coordinates of the point in the rotated frame.

1. Section 1: Introduction to
Tensor Notation and Analysis
Part 1: Coordinate transformation

2. 2
COORDINATE TRANSFORMATION
ik
j
ai +bj+ck
A vector‟s direction only makes
sense when it is compared to a
defined frame of reference or
coordinate system.

3. 3
COORDINATE TRANSFORMATION
ik
j
ai +bj+ck While we usually see these
systems defined as orthogonal to
the paper we are using, it is truly
arbitrary where we place the
coordinate system, and
sometimes it is advantageous to
put it somewhere else or in
another orientation.

4. 4
COORDINATE TRANSFORMATION
iA
j
What if we defined the coordinate
system somewhere else? For
instance, what if we translated the
“origin” from Frame A (0,0) to
Frame B (h,k)?
We know P in frame A ((x,y)
positions). What is P in B ((x‟, y‟)
positions)?
x
y
x‟
y‟
P(x,y)
B
kykPABPy
hxhPABPx
yxP
yyyy
xxxx
)0()(
)0()(
:),(
(0,0)
(h,k)

5. 5
COORDINATE TRANSFORMATION
iA
j
What if we defined the coordinate
system somewhere else? For
instance, what if we translated the
“origin” from Frame A (0,0) to
Frame B (h,k)?
We know P in frame A ((x,y)
positions). What is P in B ((x‟, y‟)
positions)?
x
y
x‟
y‟
P(x,y)
B
)(
)(
)0()(
)0()(
:),(
yy
xx
yyyy
xxxx
BAyy
BAxx
kykPABPy
hxhPABPx
yxP
(0,0)
(h,k)
If you know P(x‟,y‟) and want to find P(x,y):

6. 6
COORDINATE TRANSFORMATION
What if we rotate the
coordinate frame from A to
B?
iA
j
x
y
P(x,y)
B
(0,0)
iA
j
x
y
P(x,y)
B
(0,0)
What is P(x‟,y‟)?
For x‟, there is a component of x
that contributes (cos =cos(x‟,x))
and a component of y
(cos(90- )=sin =cos (x‟,y)
Px
Py

7. 7
COORDINATE TRANSFORMATION
A point on the x axis would have
a contribution of cos to the x‟
axis.
A point on the y axis would have
a contribution of cos (90- ) = sin
to the x‟ axis.
A point on the x axis would have a
contribution of -sin (or cos
(y‟,x)=cos 90+ ) to the y‟ coordinate.
A point on the y axis would have a
contribution of cos to the y‟
coordinate.
To find x’ value:
To find y’ value:

8. 8
Coordinate Transformation
iA
j
x
y
P(x,y)
B
(0,0)
So point P moves a net:
sincos
sincos
xy
yx
In the x‟ direction, and a net:
In the y‟ direction.
sincos
sincos
xyy
yxx

9. 9
Coordinate Transformation
Similarly, to go from (x‟,y‟) to (x,y)
A point on the x‟ axis contributes +cos
to the x coordinate.
A point on the y‟ axis contributes –sin
to the x coordinate.
A point on the x‟ axis contributes sin
to the y coordinate.
A point of the y‟ axis contributes cos
to the y coordinate.

10. 10
Coordinate Transformation
Similarly, to go from (x‟,y‟) to (x,y)
iA
j
x
y
P(x,y)
B
(0,0)
sincos
sincos
xyy
yxx

11. 11
General Coordinate Transformation
(rotation)
axes.b''anda''ebetween thangletheofcostheisb)cos(a,Where
),cos(),cos(),cos(
),cos(),cos(),cos(
),cos(),cos(),cos(
),cos(),cos(
),cos(),cos(
cossin
sincos
cossin
sincos
z
y
x
zzyzxz
zyyyxy
zxyxxx
z
y
x
y
x
yyxy
yxxx
y
x
y
x
y
x
y
x
y
x

12. 12

13. 13
Example problem
iA
j
x
y H(7,7)
B
(0,0)
= 30 deg
P(2,0)
What is position vector of P in H frame?

14. 14
First translate
iA
j
x
y H(7,7)
B
(0,0)
P(2,0)
7
5
7
7
0
2
:PpointFor
7
7
A
A
OH
OH
A
A
y
x
yy
xx
y
x
y
x
y
x
You must perform the translation first,
so that when you rotate, the arc length
a point travels is correct.

15. 15
Then rotate…
iA
j
x
y H(7,7)
B
(0,0)
P(2,0)
Then rotate:
= 30 deg
83.7
56.3
7
5
5.0867.0
867.05.0
120cos120sin
120sin120cos
5.0120cos3090cos),cos(
)120sin(867.0210cos30180cos),cos(
)120sin(867.030cos),cos(
5.0120cos3090cos),cos(
000
0000
00
000
A
A
B
B
y
x
y
x
yy
xy
yx
xx

16. How can you check your work?
1) User a ruler!
2) Rotate the paper / image so that your „new‟ frame is in a traditional position
and estimate the new values for the point
3) Recognize that while the positions of the points are vectors, the distance
between points is a scalar, and therefore independent of the coordinate
frame:
What is position vector from P-H in O frame? 5i+7j
And in the H frame? -3.56i + 7.83j
The magnitude of these position vectors (ie distance to (0,0)) is a scalar and
must be the same!
Sqrt(5*5 + 7*7)=sqrt(74)
Sqrt(3.56*3.56+7.83*7.83)=sqrt(74)
Check!