Downloaded 56 times
Uploaded bySaif Al-Kalbani
Artificial Neural Networks
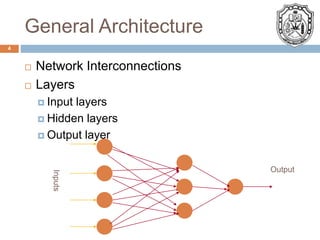
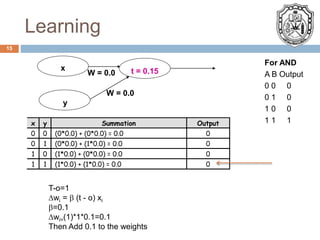
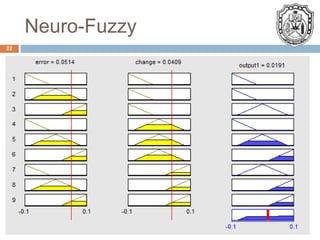
This presentation provides an overview of artificial neural networks. It discusses the general architecture including layers, activation functions, and learning methods like supervised learning. Applications mentioned include control systems, engine control units, and neuro-fuzzy hybrid systems. The strengths of neural networks are their ability to solve complex problems by learning from large amounts of input data and adapting. Some shortfalls discussed are the time required for learning and processing.
More Related Content
Similar to Artificial Neural Networks
Artificial Neural Networks
- 1. ARTIFICIAL NEURAL NETWORKS Endof Semester Presentation Presented by: Saif Al Kalbani 39579/12 20-05-2014 ECCE6206 Switching Theory: Design and Practice Spring 2014 1 Sultan Qaboos University College of Engineering Department of Electrical and Computer Engineering
- 2. Outline 2 Introduction GeneralArchitecture Learning Examples Applications Neuro-Fuzzy Conclusion
- 3. Applications 3 Input ishigh-dimensional discrete or real- valued (e.g. raw sensor input) Output is discrete or real valued Output is a vector of values Form of target function is unknown Control System Transfer function with huge number of inputs Unknown transfer function
- 4. General Architecture 4 NetworkInterconnections Layers Input layers Hidden layers Output layer Inputs Output
- 5.
- 6. General Architecture 6 Thresholdswitching units Weighted interconnections among units Highly parallel, distributed processing Learning by tuning the connection weights
- 7.
- 8. General Architecture 8 • Layers •Activation function • Learning
- 9. Layers 9 • The inputlayer. – Introduces input values into the network. – No activation function or other processing. • The hidden layer(s). – Perform classification of features – Two hidden layers are sufficient to solve any problem – Features imply more layers may be better • The output layer. – Functionally just like the hidden layers – Outputs are passed on to the world outside the neural network.
- 10.
- 11.
- 12. Learning 12 • Adjust neuralnetwork weights to map inputs to outputs. • Use a set of sample patterns where the desired output (given the inputs presented) is known. • The purpose is to learn to generalize – Recognize features which are common to good and bad exemplars – Types – Supervises – Unsupervised
- 13. Supervised Learning 13 Trainingand test data sets Training set; input & target
- 14. Learning 14 wi =wi + wi wi = (t - o) xi t=c(x) is the target value o is the perceptron output Is a small constant (e.g. 0.1) called learning rate • If the output is correct (t=o) the weights wi are not changed • If the output is incorrect (to) the weights wi are changed such that the output of the perceptron for the new weights is closer to t. The algorithm converges to the correct classification • if the training data is linearly separable and is sufficiently small
- 15. Learning 15 For AND A BOutput 0 0 0 0 1 0 1 0 0 1 1 1 t = 0.15 y x W = 0.0 W = 0.0 x y Summation Output 0 0 (0*0.0) + (0*0.0) = 0.0 0 0 1 (0*0.0) + (1*0.0) = 0.0 0 1 0 (1*0.0) + (0*0.0) = 0.0 0 1 1 (1*0.0) + (1*0.0) = 0.0 0 T-o=1 wi = (t - o) xi =0.1 wi=(1)*1*0.1=0.1 Then Add 0.1 to the weights
- 16. Learning 16 For AND A BOutput 0 0 0 0 1 0 1 0 0 1 1 1 t = 0.15 y x W = 0.1 W = 0.1 x y Summation Output 0 0 (0*0.1) + (0*0.1) = 0.0 0 0 1 (0*0.1) + (1*0.1) = 0.1 0 1 0 (1*0.1) + (0*0.1) = 0.1 0 1 1 (1*0.1) + (1*0.1) = 0.2 1
- 17.
- 18. Strength 18 Solving complexproblems Inputs are complex, large, unknown Transfer function is unknown Adaptation Adaptive controllers Learning process
- 19. Shortfalls 19 Learning Weights Processing time Delays in processing Sensing Set up Layers
- 20. Application Example 20 • EngineControl Unit (ECU) in new cars • Fuel injector • The behaviour of a car engine is influenced by a large number of parameters – temperature at various points – fuel/air mixture – lubricant viscosity. • Major companies have used neural networks to dynamically tune an engine depending on current settings.
- 21. Neuro-Fuzzy 21 Hybrid controllers ANN controllers Fuzzy logic Controllers Adaptation Rules Membership functions
- 22.
- 23. Conclusion 23 Ability ofANN to Adapt through learning Solve complex systems ANN is claimed to be able to solve any problem with a maximum of two hidden layers
- 24.
- 25.
- 26.