LR
Uploaded byLovelyn Rose
PPTX, PDF432 views

Deep learning simplified

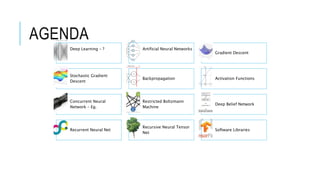
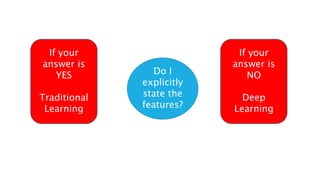
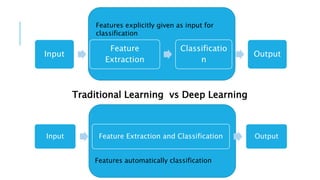
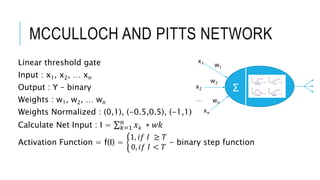
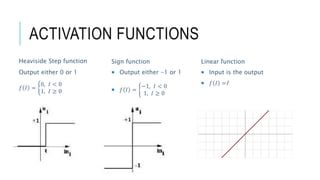
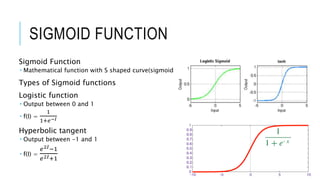
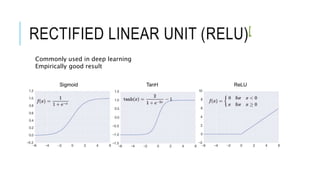
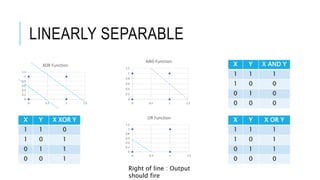
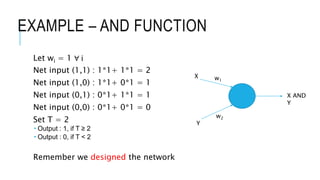
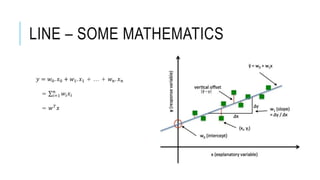
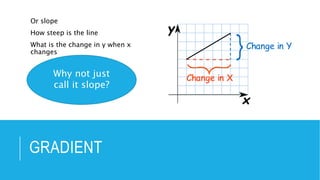
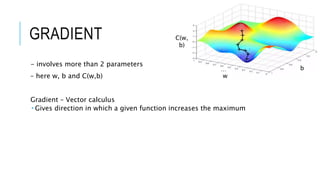
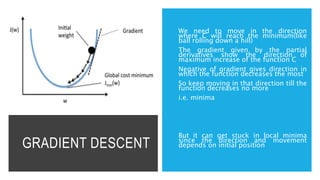
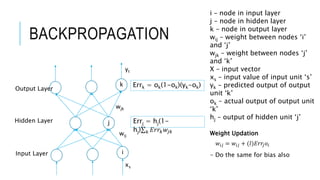
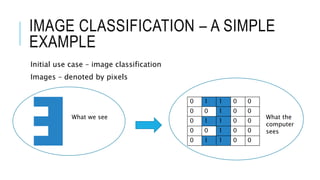
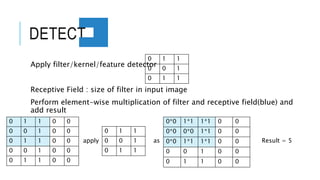
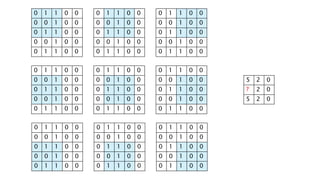
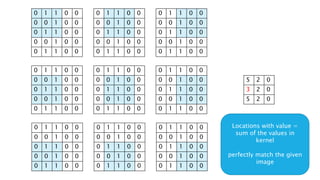
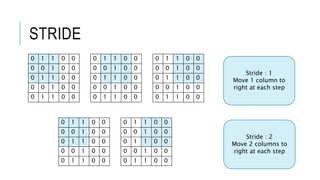
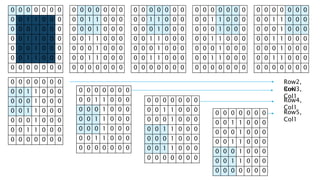
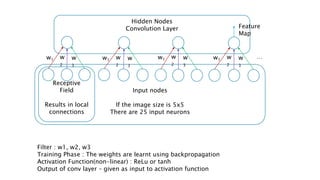
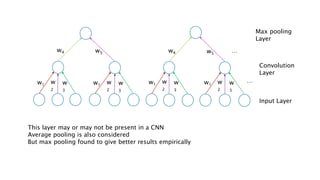
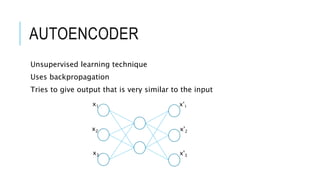
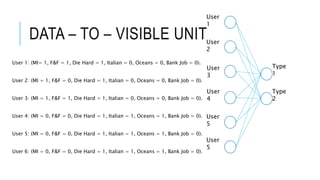
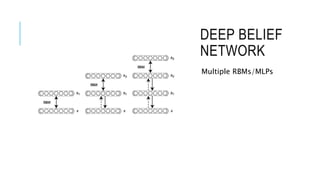
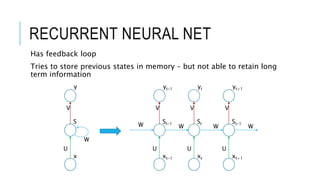
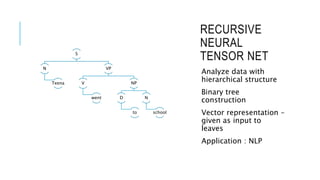
The document discusses deep learning and artificial neural networks. It provides an agenda for topics covered, including gradient descent, backpropagation, activation functions, and examples of neural network architectures like convolutional neural networks. It explains concepts like how neural networks learn patterns from data using techniques like stochastic gradient descent to minimize loss functions. Deep learning requires large amounts of processing power and labeled training data. Common deep learning networks are used for tasks like image recognition, object detection, and time series analysis.

Data & Analytics◦
Related topics:
Deep Learning•

Embed presentation

Downloaded 18 times
DEEP LEARNING Dr.S.Lovelyn Rose Associate Professor Dept. of CSE PSG CT, Cbe.
AGENDA Deep Learning – ? Artificial Neural Networks Gradient Descent Stochastic Gradient Descent Backpropagation Activation Functions Concurrent Neural Network – Eg. Restricted Boltzmann Machine Deep Belief Network Recurrent Neural Net Recursive Neural Tensor Net Software Libraries
WITH AND WITHOUT DEEP LEARNING Features  Crest  Hoof  Muscular legs  Muzzle  Lush tail Do I explicitly state the features?
Do I explicitly state the features? If your answer is NO Deep Learning If your answer is YES Traditional Learning
Input Feature Extraction Classificatio n Output Input Feature Extraction and Classification Output Traditional Learning vs Deep Learning Features explicitly given as input for classification Features automatically classification
Processing Power Very parallel Fast Cheap Performance benchmark PC CPU – 1 -3 Gflops/sec average GPU – 100 Gflops/sec average A FEASIBILITY STUDY Deep learning requires lot of • Processing power • Training data Training Data
ARTIFICIAL NEURAL NETWORKS
MCCULLOCH AND PITTS NETWORK Linear threshold gate Input : x1, x2, … xn Output : Y – binary Weights : w1, w2, … wn Weights Normalized : (0,1), (-0.5,0.5), (-1,1) Calculate Net Input : I = 𝑘=1 𝑛 𝑥 𝑘 ∗ 𝑤𝑘 Activation Function = f(I) = 1, 𝑖𝑓 𝐼 ≥ 𝑇 0, 𝑖𝑓 𝐼 < 𝑇 - binary step function Σ xn x2 x1 … w1 w2 wn
ACTIVATION FUNCTIONS Heaviside Step function Output either 0 or 1 𝑓 𝐼 = 0, 𝐼 < 0 1, 𝐼 ≥ 0 Linear function  Input is the output  𝑓 𝐼 =I Sign function  Output either -1 or 1  𝑓 𝐼 = −1, 𝐼 < 0 1, 𝐼 ≥ 0
SIGMOID FUNCTION Sigmoid Function  Mathematical function with S shaped curve(sigmoid curve) Types of Sigmoid functions Logistic function  Output between 0 and 1  f(I) = 1 1+𝑒−𝐼 Hyperbolic tangent  Output between -1 and 1  f(I) = 𝑒2𝐼−1 𝑒2𝐼+1
RECTIFIED LINEAR UNIT (RELU)[ Commonly used in deep learning Empirically good result
LINEARLY SEPARABLE X Y X AND Y 1 1 1 1 0 0 0 1 0 0 0 0 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 AND Function X Y X OR Y 1 1 1 1 0 1 0 1 1 0 0 0 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 OR Function X Y X XOR Y 1 1 0 1 0 1 0 1 1 0 0 1 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 XOR Function Right of line : Output should fire
EXAMPLE – AND FUNCTION Let wi = 1 ∀ i Net input (1,1) : 1*1+ 1*1 = 2 Net input (1,0) : 1*1+ 0*1 = 1 Net input (0,1) : 0*1+ 1*1 = 1 Net input (0,0) : 0*1+ 0*1 = 0 Set T = 2  Output : 1, if T ≥ 2  Output : 0, if T < 2 Remember we designed the network X Y X AND Y w1 w2
QUESTION TIME What changes do you need to make to implement an OR function
LINE – SOME MATHEMATICS 𝑦 = 𝑤0. 𝑥0 + 𝑤1. 𝑥1 + … + 𝑤 𝑛. 𝑥 𝑛 = 𝑖=1 𝑛 𝑤𝑖 𝑥𝑖 = 𝑤 𝑇 𝑥
INTRODUCING BIAS Classifier tries to find line to separate classes y=mx+c In training phase neural network tries to learn appropriate weights to draw the line If there is no y intercept, any line we draw will pass through origin So introduce y-intercept as bias If we set the bias to 1 then why does it make difference to the fit now that every line will now go through (0,1) instead of (0,0) by multiplying a bias by a weight, you can shift it by an arbitrary amount
BIAS AND THE SIGMOID FUNCTION (x1,x2) = (0.2, 0.5) (w0,w1,w2) = (0.4, 0.3, 0.5) b = 1 Net input : I = 1*0.4 + 0.2*0.3 + 0.5*0.5 = 0.71 y = 1 1+ 𝑒−𝐼 = 1 1+ 𝑒−0.71 = 0.67 x1 x2 y w1 w2 w0 b
PERCEPTRON Binary classifier Let input x = ( x1, x2, ... , xn) where each xi = 0 or 1. And let output y = 0 or 1. Algorithm is repeat forever:  Given input x = ( x1, x2, ... , xn).  Perceptron produces output y.  The correct output is O.  If we had wrong answer, change wi's and T, otherwise do nothing. Single layer perceptron solves only linearly separable problems
HOW TO CHANGE wi y – Predicted output – 0.67 O – Actual output – 1 Change wi based on (O-y) Use error function to connect actual and predicted output
ERROR FUNCTION/LOSS FUNCTION/COST FUNCTION Given data set with ‘n’ input Error = Mean Square Error C = 1 𝑛 𝑖=1 𝑛 (𝑜𝑖 − 𝑦𝑖)2 C(w,b) = 1 𝑛 𝑖=1 𝑛 (𝑜𝑖 − (𝑤 𝑇 𝑥 + 𝑏))2 = 1 𝑛 𝑥(𝑜 − 𝑦) w – collection of weights in the network b – collection of bias o – vector of actual(desired) output y – vector of predicted output when x is input - dependent on w, b Why error function? Why not do it directly? - error functions help to figure how small changes in w and b change the number of samples correctly classified
OBJECTIVE - Minimize error function - Minimize C(w,b) - Perfect if the C(w,b) = 0 - Good if C(w,b) ≈ 0 - i.e Find weights and bias such that C(w,b) ≈ 0 - To do this use “Gradient Descent”
GRADIENT DESCENT
GRADIENT Or slope How steep is the line What is the change in y when x changes Why not just call it slope?
GRADIENT - involves more than 2 parameters – here w, b and C(w,b) Gradient – Vector calculus  Gives direction in which a given function increases the maximum w w b C(w, b)
BACKGROUND If F is a function with variable x Rate of change of F w.r.t x is 𝑑𝐹 𝑑𝑥 i.e how much to move in the x direction i.e to the right If C has variables w, b Direction to move give by ( 𝜕𝐶 𝜕𝑤 , 𝜕𝐶 𝜕𝑏 ) These are partial derivatives (i.e keep other variables constant) This gives direction of movement in the direction of w and b
GRADIENT DESCENT We need to move in the direction where C will reach the minimum(like ball rolling down a hill) The gradient given by the partial derivatives show the direction of maximum increase of the function C Negative of gradient gives direction in which the function decreases the most So keep moving in that direction till the function decreases no more i.e. minima But it can get stuck in local minima since the direction and movement depends on initial position
HOW MUCH TO MOVE New_W = old_W + 𝜕𝐶 𝜕𝑤 New_b = old_b + 𝜕𝐶 𝜕𝑏 Or New_W = old_W + l 𝜕𝐶 𝜕𝑤 ‘l’ is the learning rate that decides how big a step to take towards the minima
STOCHASTIC GRADIENT DESCENT Instead of taking the entire training set before performing a move along minima, SGD takes a random set of samples before making a move. Variations 1. Take 1 training sample at a time 2. Batch SGD – take a random set of subsamples
BACKPROPAGATION i j k wij wjk Input Layer Hidden Layer Output Layer yt xs i – node in input layer j – node in hidden layer k – node in output layer wij – weight between nodes ‘i’ and ‘j’ wjk – weight between nodes ‘j’ and ‘k’ X – input vector xs – input value of input unit ‘s’ yk – predicted output of output unit ‘k’ ok – actual output of output unit ‘k’ hj – output of hidden unit ‘j’ Errk = ok(1-ok)(yk-ok) Errj = hj(1- hj) 𝑘 𝐸𝑟𝑟𝑘 𝑤𝑗𝑘 𝑤𝑖𝑗 = 𝑤𝑖𝑗 + (𝑙)𝐸𝑟𝑟𝑗 𝑜𝑖 Weight Updation - Do the same for bias also
TYPES OF NEURAL NETWORKS Feed forward network  Information goes only in one direction Single layer perceptron  information goes from input  output  Only 1 output layer  Nodes in output layer are processing elements – with activation function Multilayer perceptron(MLP)  Multiple layers of nodes in a directed graph  Can distinguish non-linearly separable data  Nodes in hidden and output layers – processing elements – with nonlinear activation functions  Input  hidden  output
COMMON DEEP LEARNING NETWORKS WITH APPLICATIONS Extract patterns from unlabeled data  Restricted Boltzmann Machine  Autoencoder Classification from labelled data  Recurrent neural net  Recursive neural tensor network Image recognition  Deep belief network  Convolutional neural network Object recognition  Convolutional neural network  Recursive neural tensor network Speech Recognition/Time series analysis  Recurrent neural net
CONVOLUTIONAL NEURAL NETWORK
IMAGE CLASSIFICATION – A SIMPLE EXAMPLE Initial use case – image classification Images – denoted by pixels 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 What we see What the computer sees
DETECT Apply filter/kernel/feature detector Receptive Field : size of filter in input image Perform element-wise multiplication of filter and receptive field(blue) and add result 0 1 1 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 apply 0 1 1 0 0 1 0 1 1 as 0*0 1*1 1*1 0 0 0*0 0*0 1*1 0 0 0*0 1*1 1*1 0 0 0 0 1 0 0 0 1 1 0 0 Result = 5
0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 5 2 0 ? 2 0 5 2 0
0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 5 2 0 3 2 0 5 2 0 Locations with value = sum of the values in kernel perfectly match the given image
0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 Stride : 1 Move 1 column to right at each step STRIDE 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 Stride : 2 Move 2 columns to right at each step
ZERO PADDING Size of output = 3x3 If the input matrix is a 10x10 matrix then the output matrix size = ?
ZERO PADDING Size of output = 3x3 If the input matrix is a 10x10 matrix then the output matrix size = 7x7 What if Size of output matrix should be equal to the size of the input matrix? The actual first element should be at the middle when the filter is first applied. So pad top, left etc with ‘0’, such that filter can be applied with every actual element
0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 Row2, Col1Row3, Col1 Row4, Col1 Row5, Col1
WHAT’S ALL THIS GOT TO DO WITH CNN? Matrix after applying filter on different receptive fields = convolved matrix Also called activation map/feature map In our example is the feature map when 9 filters are applied. Or example is analogous to the working of convolution layer. Input to convolution layer : image Output : Value after applying filter 5 2 0 3 2 0 5 2 0
BUT… Deep learning does not require the programmer to provide the feature – i.e. in our case – the filter So - the filter needs to be learnt by the neural network model and not given as input
Hidden Nodes Convolution Layer Input nodes If the image size is 5x5 There are 25 input neurons Receptive Field Results in local connections w1 w 2 w 3 w1 w 2 w 3 w1 w 2 w 3 w1 w 2 w 3 Feature Map Filter : w1, w2, w3 Training Phase : The weights are learnt using backpropagation Activation Function(non-linear) : ReLu or tanh Output of conv layer – given as input to activation function …
5 2 0 3 2 0 5 2 0 MAX POOLING Max pool with 2x2 filter and stride 1 i.e take max of every 2x2 filter 5 2 5 2 This results in downsampling and detecting more abstract features While the filter in the conv layer might detect edges This layer may detect more abstract things like objects 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 It has actually found the similarity between the upper and lower portions of the image
w1 w 2 w 3 w1 w 2 w 3 w1 w 2 w 3 w1 w 2 w 3 w4 w5 w4 w5 Input Layer Convolution Layer Max pooling Layer This layer may or may not be present in a CNN Average pooling is also considered But max pooling found to give better results empirically … …
A PARTIAL CNN WITH MANY HIDDEN LAYERS Has multiple hidden layers of convolution layers and max pooling layers Different filters applied in different layers Example Partial CNN Input Conv layer Conv layer Max pooling Conv layer Conv layer Max pooling …
FULLY CONNECTED LAYER Last layer Neurons in this layer are fully connected to all neurons in the previous layer They can have different weights and bias as normal ANN The weights are multiplied with the output of the previous layer and bias is added – which is input to the activation function
OUTPUT Usually multiple neurons – based on the number of classes - each outputs probability with which a class occurs If differentiate horse or not 2 output neurons – with probability with which the image is/is not a horse Input Conv layer Conv layer Max pooling Conv layer Conv layer Max pooling Fully connected layer
OUTLINE OF OTHER NETWORKS
AUTOENCODER Unsupervised learning technique Uses backpropagation Tries to give output that is very similar to the input x1 x2 x3 x'1 x'2 x'3
RESTRICTED BOLTZMANN MACHINE Shallow 2 layer net Connections  Fully connected  Every node in visible layer connected to every node in hidden layer  Undirected  Restricted – no connection between nodes in a layer Training : Uses contrastive divergence or approximate gradient descent
Action Heist
DATA – TO – VISIBLE UNIT User 1: (MI= 1, F&F = 1, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). User 2: (MI = 1, F&F = 0, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). User 3: (MI = 1, F&F = 1, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). User 4: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). User 5: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). User 6: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). User 1 User 2 User 3 User 4 User 5 User 5 Type 1 Type 2
HIDDEN UNIT – TYPE OF MOVIE INTERESTED IN • User 1: (MI = 1, F&F = 1, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). Likes action movies • User 2: (MI = 1, F&F = 0, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). Prefers action movies, but doesn’t like F&F. • User 3: (MI = 1, F&F = 1, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). Likes action movies. • User 4: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). Generally likes heist movies. • User 5: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). Generally likes heist movies. • User 6: (MI = 0, F&F = 0, Die Hard = 0, Italian = 1, Oceans = 1, Bank Job = 1). Likes heist movies. Based on the type liked the corresponding hidden unit is activated more
DEEP BELIEF NETWORK Multiple RBMs/MLPs
RECURRENT NEURAL NET Used when input seen as a sequence of data rather than as a bag of elements Activation Function : tanh or ReLu Learning weights : Back Propagation Through Time(BPTT) Problem : Vanishing Gradient, Exploding Gradient Solutions : Long Short Term Memory(LSTM), Gated Recurrent Units(GRU) Applications : NLP, Machine Translation, Speech Recognition
RECURRENT NEURAL NET Has feedback loop Tries to store previous states in memory – but not able to retain long term information W U V W St-1 yt-1 xt-1 U V W St yt xt U V W St-1 yt+1 xt+1 U V W S y x
PARAMETERS IN THE NETWORK xt – input at time unit ‘t’ st – hidden state at time unit ‘t’ - input to st is (u.xt +w. st-1) which is passed through activation function s-1 = all zeros – initially yt – output at time unit ‘t’ = softmax(v.st)
RECURSIVE NEURAL TENSOR NET Analyze data with hierarchical structure Binary tree construction Vector representation – given as input to leaves Application : NLP S N Teena VP V went NP D to N school
REFERENCES http://blog.echen.me/2011/07/18/introduction-to-restricted-boltzmann- machines/ http://cs231n.github.io/neural-networks-1/ http://cs231n.github.io/convolutional-networks/ http://www.wildml.com/2015/11/understanding-convolutional-neural- networks-for-nlp/ http://colah.github.io/posts/2014-07-Conv-Nets-Modular/ https://adeshpande3.github.io/adeshpande3.github.io/A-Beginner's-Guide-To- Understanding-Convolutional-Neural-Networks/ http://colah.github.io/posts/2014-07-Understanding-Convolutions/
REFERENCES https://github.com/adeshpande3/Tensorflow-Programs-and- Tutorials/blob/master/Convolutional%20Neural%20Networks.ipynb http://neuralnetworksanddeeplearning.com/chap1.html https://betterexplained.com/articles/vector-calculus-understanding- the-gradient/ http://www.wildml.com/2015/09/recurrent-neural-networks- tutorial-part-1-introduction-to-rnns/
TO ACCESS THE PPT https://www.slideshare.net/lovelynrose/deep-learning-simplified

More Related Content

PPTX
Deep neural networks & computational graphs
byRevanth Kumar
 
PPTX
Introduction to Deep learning and H2O for beginner's
byVidyasagar Bhargava
 
PPTX
Deep Learning Interview Questions And Answers | AI & Deep Learning Interview ...
bySimplilearn
 
PPTX
Deep learning algorithms
byRevanth Kumar
 
PDF
The Back Propagation Learning Algorithm
byESCOM
 
PDF
Deep Style: Using Variational Auto-encoders for Image Generation
byTJ Torres
 
PDF
APPLIED MACHINE LEARNING
byRevanth Kumar
 
PPTX
Introduction to Neural networks (under graduate course) Lecture 7 of 9
byRanda Elanwar
 
Deep neural networks & computational graphs
byRevanth Kumar
 
Introduction to Deep learning and H2O for beginner's
byVidyasagar Bhargava
 
Deep Learning Interview Questions And Answers | AI & Deep Learning Interview ...
bySimplilearn
 
Deep learning algorithms
byRevanth Kumar
 
The Back Propagation Learning Algorithm
byESCOM
 
Deep Style: Using Variational Auto-encoders for Image Generation
byTJ Torres
 
APPLIED MACHINE LEARNING
byRevanth Kumar
 
Introduction to Neural networks (under graduate course) Lecture 7 of 9
byRanda Elanwar
 

What's hot

PPT
backpropagation in neural networks
byAkash Goel
 
PDF
Learning in Networks: were Pavlov and Hebb right?
byVictor Miagkikh
 
PPTX
Backpropagation And Gradient Descent In Neural Networks | Neural Network Tuto...
bySimplilearn
 
PPTX
02 image processing
byankit_ppt
 
PPTX
06 image features
byankit_ppt
 
PPT
Mitchell's Face Recognition
bybutest
 
PPTX
Ot regularization and_gradient_descent
byankit_ppt
 
PDF
Introduction to Applied Machine Learning
bySheilaJimenezMorejon
 
PDF
Backpropagation in Convolutional Neural Network
byHiroshi Kuwajima
 
PDF
Multi Layer Perceptron & Back Propagation
bySung-ju Kim
 
PPT
Principles of soft computing-Associative memory networks
bySivagowry Shathesh
 
PPTX
Neural network
bymarada0033
 
PPTX
Machine Learning Essentials Demystified part2 | Big Data Demystified
byOmid Vahdaty
 
PDF
Artificial neural networks
byarjitkantgupta
 
PPTX
The Art Of Backpropagation
byJennifer Prendki
 
PDF
Deep Feed Forward Neural Networks and Regularization
byYan Xu
 
PPTX
Introduction to Neural networks (under graduate course) Lecture 8 of 9
byRanda Elanwar
 
PPTX
Machine Learning Essentials Demystified part1 | Big Data Demystified
byOmid Vahdaty
 
PPTX
Neural net and back propagation
byMohit Shrivastava
 
PPT
Back propagation
byNagarajan
 
backpropagation in neural networks
byAkash Goel
 
Learning in Networks: were Pavlov and Hebb right?
byVictor Miagkikh
 
Backpropagation And Gradient Descent In Neural Networks | Neural Network Tuto...
bySimplilearn
 
02 image processing
byankit_ppt
 
06 image features
byankit_ppt
 
Mitchell's Face Recognition
bybutest
 
Ot regularization and_gradient_descent
byankit_ppt
 
Introduction to Applied Machine Learning
bySheilaJimenezMorejon
 
Backpropagation in Convolutional Neural Network
byHiroshi Kuwajima
 
Multi Layer Perceptron & Back Propagation
bySung-ju Kim
 
Principles of soft computing-Associative memory networks
bySivagowry Shathesh
 
Neural network
bymarada0033
 
Machine Learning Essentials Demystified part2 | Big Data Demystified
byOmid Vahdaty
 
Artificial neural networks
byarjitkantgupta
 
The Art Of Backpropagation
byJennifer Prendki
 
Deep Feed Forward Neural Networks and Regularization
byYan Xu
 
Introduction to Neural networks (under graduate course) Lecture 8 of 9
byRanda Elanwar
 
Machine Learning Essentials Demystified part1 | Big Data Demystified
byOmid Vahdaty
 
Neural net and back propagation
byMohit Shrivastava
 
Back propagation
byNagarajan
 

Similar to Deep learning simplified

PPT
Lecture2---Feed-Forward Neural Networks.ppt
byKassahunAwoke
 
PPTX
Artificial neural networks - A gentle introduction to ANNS.pptx
byAttaNox1
 
PPT
ch11.pptKGYUTFYDRERLJIOUY7T867RVHOJIP09-IU08Y7GTFGYU890-I90UIYGUI
byAbodahab
 
PPT
ch11.ppt kusrdsdagrfzgfdfgdfsdsfdsxgdhfjgh50s
byAbodahab
 
PPT
Artificial Neural Network
byPratik Aggarwal
 
PDF
ARTIFICIAL-NEURAL-NETWORKMACHINELEARNING
bymohanapriyastp
 
PDF
Artificial Neural Networks
byStefano Dalla Palma
 
PPT
SOFTCOMPUTERING TECHNICS - Unit
bysravanthi computers
 
PPTX
3. ANNs (2)Artificial neural networks for phd course
byLaraibRazzaq3
 
PPTX
Learning to Rank with Neural Networks
byBhaskar Mitra
 
PDF
W2 - Multilayer Neural Network Lecture notes university of sydney
bymayanksharmadav
 
PPTX
latest TYPES OF NEURAL NETWORKS (2).pptx
byMdMahfoozAlam5
 
PDF
[DSC 2016] 系列活動：李宏毅 / 一天搞懂深度學習
by台灣資料科學年會
 
PDF
Deep Learning and Design Thinking
byYen-lung Tsai
 
PPTX
Neural Networks
byMakerere Unversity School of Public Health, Victoria University
 
PDF
The human brain in the national TV , how to become the next hokage
byarazik1
 
PPTX
Deep learning study 2
bySan Kim
 
PDF
Neural-Network(Basics) -Pdf lecture notes-IIT patna.pdf
byPradipSaha48
 
PDF
Machine Learning.pdf
bynikola_tesla1
 
PDF
NN-Ch2.PDF
bygnans Kgnanshek
 
Lecture2---Feed-Forward Neural Networks.ppt
byKassahunAwoke
 
Artificial neural networks - A gentle introduction to ANNS.pptx
byAttaNox1
 
ch11.pptKGYUTFYDRERLJIOUY7T867RVHOJIP09-IU08Y7GTFGYU890-I90UIYGUI
byAbodahab
 
ch11.ppt kusrdsdagrfzgfdfgdfsdsfdsxgdhfjgh50s
byAbodahab
 
Artificial Neural Network
byPratik Aggarwal
 
ARTIFICIAL-NEURAL-NETWORKMACHINELEARNING
bymohanapriyastp
 
Artificial Neural Networks
byStefano Dalla Palma
 
SOFTCOMPUTERING TECHNICS - Unit
bysravanthi computers
 
3. ANNs (2)Artificial neural networks for phd course
byLaraibRazzaq3
 
Learning to Rank with Neural Networks
byBhaskar Mitra
 
W2 - Multilayer Neural Network Lecture notes university of sydney
bymayanksharmadav
 
latest TYPES OF NEURAL NETWORKS (2).pptx
byMdMahfoozAlam5
 
[DSC 2016] 系列活動：李宏毅 / 一天搞懂深度學習
by台灣資料科學年會
 
Deep Learning and Design Thinking
byYen-lung Tsai
 
Neural Networks
byMakerere Unversity School of Public Health, Victoria University
 
The human brain in the national TV , how to become the next hokage
byarazik1
 
Deep learning study 2
bySan Kim
 
Neural-Network(Basics) -Pdf lecture notes-IIT patna.pdf
byPradipSaha48
 
Machine Learning.pdf
bynikola_tesla1
 
NN-Ch2.PDF
bygnans Kgnanshek
 

More from Lovelyn Rose

PPTX
Mergesort without Animation
byLovelyn Rose
 
PPTX
Problem solving
byLovelyn Rose
 
PPTX
Placement oriented data structures
byLovelyn Rose
 
PPTX
Linked list
byLovelyn Rose
 
PPTX
Insertion and Deletion in Binary Search Trees (using Arrays and Linked Lists)
byLovelyn Rose
 
PPTX
Linked list without animation
byLovelyn Rose
 
Mergesort without Animation
byLovelyn Rose
 
Problem solving
byLovelyn Rose
 
Placement oriented data structures
byLovelyn Rose
 
Linked list
byLovelyn Rose
 
Insertion and Deletion in Binary Search Trees (using Arrays and Linked Lists)
byLovelyn Rose
 
Linked list without animation
byLovelyn Rose
 

Recently uploaded

PPTX
I need all your support to get the data for the sections like photo gallery o...
byhsharsha1
 
PDF
Understanding Data Analytics: Concepts, Types, and Use Cases
byThe IoT Academy
 
PDF
SF User Group - Account-Contact Relationship Feb 2026
byLukas Lunow
 
PPTX
Query Parsing: The SEO Gatekeeper That Decides Rankings
bySemantic SEO BD
 
PPTX
Lecture 14- Introduction to Hypothesis Testing.pptx
bygbadamosiayomide
 
PDF
Step by Step Guide to Buying a Old or Aged Verified Paxful Accounts in US.pdf
byTopSelleriTDotCom
 
PPTX
Reading and Writing Skills - Critical Reading ppt.pptx
byMargieJavier2
 
PDF
PathRAG rag pipeline PathRAG rag pipeline .pdf
byhotslix023
 
PPTX
250106204341-c238c4fadonebeforelastyear.pptx
byAbduRouf3
 
PDF
US Digital Fan Engagement Index 2026: Benchmarking Online Demand for Sports T...
byHyperset Group Ltd
 
PDF
Analysis of Union Budget 2026-27: Major Announcements and their Impact
byDeeshiPavecha
 
PDF
Khan Traders Fish Meal – MSDS Material Safety Data Sheet
byKhan Traders Karachi
 
PPT
data collection tool ppt.ppttttdataadfttg
byMuhammadodil
 
PPTX
GENPHYSICS-2.pptx this about general physics. Grade 11 lesson
byGwynMorata
 
PPTX
Organizational Structure and Design Topic 4
bydavenieralayaay
 
PDF
Machine_Psychology_2050_Strategic_Scenarios.pdf
byKambs Consulting
 
PDF
Trustworthy AI : Governance of AI through Ethics
byKarim Baïna
 
PPTX
Social Media Audit of Starbucks Coffee Company.pptx
bydiviap21
 
PDF
LECTURE - Overcoming the AI Failure Rate - AIG, DQM.pdf
bySami Laine
 
PDF
Data Science vs Machine Learning vs AI | Industry Skills Explained
bymuhsinam9074
 
I need all your support to get the data for the sections like photo gallery o...
byhsharsha1
 
Understanding Data Analytics: Concepts, Types, and Use Cases
byThe IoT Academy
 
SF User Group - Account-Contact Relationship Feb 2026
byLukas Lunow
 
Query Parsing: The SEO Gatekeeper That Decides Rankings
bySemantic SEO BD
 
Lecture 14- Introduction to Hypothesis Testing.pptx
bygbadamosiayomide
 
Step by Step Guide to Buying a Old or Aged Verified Paxful Accounts in US.pdf
byTopSelleriTDotCom
 
Reading and Writing Skills - Critical Reading ppt.pptx
byMargieJavier2
 
PathRAG rag pipeline PathRAG rag pipeline .pdf
byhotslix023
 
250106204341-c238c4fadonebeforelastyear.pptx
byAbduRouf3
 
US Digital Fan Engagement Index 2026: Benchmarking Online Demand for Sports T...
byHyperset Group Ltd
 
Analysis of Union Budget 2026-27: Major Announcements and their Impact
byDeeshiPavecha
 
Khan Traders Fish Meal – MSDS Material Safety Data Sheet
byKhan Traders Karachi
 
data collection tool ppt.ppttttdataadfttg
byMuhammadodil
 
GENPHYSICS-2.pptx this about general physics. Grade 11 lesson
byGwynMorata
 
Organizational Structure and Design Topic 4
bydavenieralayaay
 
Machine_Psychology_2050_Strategic_Scenarios.pdf
byKambs Consulting
 
Trustworthy AI : Governance of AI through Ethics
byKarim Baïna
 
Social Media Audit of Starbucks Coffee Company.pptx
bydiviap21
 
LECTURE - Overcoming the AI Failure Rate - AIG, DQM.pdf
bySami Laine
 
Data Science vs Machine Learning vs AI | Industry Skills Explained
bymuhsinam9074
 

Deep learning simplified

  • 1.
    DEEP LEARNING Dr.S.Lovelyn Rose AssociateProfessor Dept. of CSE PSG CT, Cbe.
  • 2.
    AGENDA Deep Learning –? Artificial Neural Networks Gradient Descent Stochastic Gradient Descent Backpropagation Activation Functions Concurrent Neural Network – Eg. Restricted Boltzmann Machine Deep Belief Network Recurrent Neural Net Recursive Neural Tensor Net Software Libraries
  • 3.
    WITH AND WITHOUTDEEP LEARNING Features  Crest  Hoof  Muscular legs  Muzzle  Lush tail Do I explicitly state the features?
  • 4.
    Do I explicitly state the features? Ifyour answer is NO Deep Learning If your answer is YES Traditional Learning
  • 5.
    Input Feature Extraction Classificatio n Output Input Feature Extractionand Classification Output Traditional Learning vs Deep Learning Features explicitly given as input for classification Features automatically classification
  • 6.
    Processing Power Very parallel Fast Cheap Performancebenchmark PC CPU – 1 -3 Gflops/sec average GPU – 100 Gflops/sec average A FEASIBILITY STUDY Deep learning requires lot of • Processing power • Training data Training Data
  • 7.
  • 8.
    MCCULLOCH AND PITTSNETWORK Linear threshold gate Input : x1, x2, … xn Output : Y – binary Weights : w1, w2, … wn Weights Normalized : (0,1), (-0.5,0.5), (-1,1) Calculate Net Input : I = 𝑘=1 𝑛 𝑥 𝑘 ∗ 𝑤𝑘 Activation Function = f(I) = 1, 𝑖𝑓 𝐼 ≥ 𝑇 0, 𝑖𝑓 𝐼 < 𝑇 - binary step function Σ xn x2 x1 … w1 w2 wn
  • 9.
    ACTIVATION FUNCTIONS Heaviside Stepfunction Output either 0 or 1 𝑓 𝐼 = 0, 𝐼 < 0 1, 𝐼 ≥ 0 Linear function  Input is the output  𝑓 𝐼 =I Sign function  Output either -1 or 1  𝑓 𝐼 = −1, 𝐼 < 0 1, 𝐼 ≥ 0
  • 10.
    SIGMOID FUNCTION Sigmoid Function Mathematical function with S shaped curve(sigmoid curve) Types of Sigmoid functions Logistic function  Output between 0 and 1  f(I) = 1 1+𝑒−𝐼 Hyperbolic tangent  Output between -1 and 1  f(I) = 𝑒2𝐼−1 𝑒2𝐼+1
  • 11.
    RECTIFIED LINEAR UNIT(RELU)[ Commonly used in deep learning Empirically good result
  • 12.
    LINEARLY SEPARABLE X YX AND Y 1 1 1 1 0 0 0 1 0 0 0 0 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 AND Function X Y X OR Y 1 1 1 1 0 1 0 1 1 0 0 0 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 OR Function X Y X XOR Y 1 1 0 1 0 1 0 1 1 0 0 1 0 0.2 0.4 0.6 0.8 1 1.2 0 0.5 1 1.5 XOR Function Right of line : Output should fire
  • 13.
    EXAMPLE – ANDFUNCTION Let wi = 1 ∀ i Net input (1,1) : 1*1+ 1*1 = 2 Net input (1,0) : 1*1+ 0*1 = 1 Net input (0,1) : 0*1+ 1*1 = 1 Net input (0,0) : 0*1+ 0*1 = 0 Set T = 2  Output : 1, if T ≥ 2  Output : 0, if T < 2 Remember we designed the network X Y X AND Y w1 w2
  • 14.
    QUESTION TIME What changesdo you need to make to implement an OR function
  • 15.
    LINE – SOMEMATHEMATICS 𝑦 = 𝑤0. 𝑥0 + 𝑤1. 𝑥1 + … + 𝑤 𝑛. 𝑥 𝑛 = 𝑖=1 𝑛 𝑤𝑖 𝑥𝑖 = 𝑤 𝑇 𝑥
  • 16.
    INTRODUCING BIAS Classifier triesto find line to separate classes y=mx+c In training phase neural network tries to learn appropriate weights to draw the line If there is no y intercept, any line we draw will pass through origin So introduce y-intercept as bias If we set the bias to 1 then why does it make difference to the fit now that every line will now go through (0,1) instead of (0,0) by multiplying a bias by a weight, you can shift it by an arbitrary amount
  • 17.
    BIAS AND THESIGMOID FUNCTION (x1,x2) = (0.2, 0.5) (w0,w1,w2) = (0.4, 0.3, 0.5) b = 1 Net input : I = 1*0.4 + 0.2*0.3 + 0.5*0.5 = 0.71 y = 1 1+ 𝑒−𝐼 = 1 1+ 𝑒−0.71 = 0.67 x1 x2 y w1 w2 w0 b
  • 18.
    PERCEPTRON Binary classifier Let inputx = ( x1, x2, ... , xn) where each xi = 0 or 1. And let output y = 0 or 1. Algorithm is repeat forever:  Given input x = ( x1, x2, ... , xn).  Perceptron produces output y.  The correct output is O.  If we had wrong answer, change wi's and T, otherwise do nothing. Single layer perceptron solves only linearly separable problems
  • 19.
    HOW TO CHANGEwi y – Predicted output – 0.67 O – Actual output – 1 Change wi based on (O-y) Use error function to connect actual and predicted output
  • 20.
    ERROR FUNCTION/LOSS FUNCTION/COST FUNCTION Givendata set with ‘n’ input Error = Mean Square Error C = 1 𝑛 𝑖=1 𝑛 (𝑜𝑖 − 𝑦𝑖)2 C(w,b) = 1 𝑛 𝑖=1 𝑛 (𝑜𝑖 − (𝑤 𝑇 𝑥 + 𝑏))2 = 1 𝑛 𝑥(𝑜 − 𝑦) w – collection of weights in the network b – collection of bias o – vector of actual(desired) output y – vector of predicted output when x is input - dependent on w, b Why error function? Why not do it directly? - error functions help to figure how small changes in w and b change the number of samples correctly classified
  • 21.
    OBJECTIVE - Minimize errorfunction - Minimize C(w,b) - Perfect if the C(w,b) = 0 - Good if C(w,b) ≈ 0 - i.e Find weights and bias such that C(w,b) ≈ 0 - To do this use “Gradient Descent”
  • 22.
  • 23.
    GRADIENT Or slope How steepis the line What is the change in y when x changes Why not just call it slope?
  • 24.
    GRADIENT - involves morethan 2 parameters – here w, b and C(w,b) Gradient – Vector calculus  Gives direction in which a given function increases the maximum w w b C(w, b)
  • 25.
    BACKGROUND If F isa function with variable x Rate of change of F w.r.t x is 𝑑𝐹 𝑑𝑥 i.e how much to move in the x direction i.e to the right If C has variables w, b Direction to move give by ( 𝜕𝐶 𝜕𝑤 , 𝜕𝐶 𝜕𝑏 ) These are partial derivatives (i.e keep other variables constant) This gives direction of movement in the direction of w and b
  • 26.
    GRADIENT DESCENT We needto move in the direction where C will reach the minimum(like ball rolling down a hill) The gradient given by the partial derivatives show the direction of maximum increase of the function C Negative of gradient gives direction in which the function decreases the most So keep moving in that direction till the function decreases no more i.e. minima But it can get stuck in local minima since the direction and movement depends on initial position
  • 27.
    HOW MUCH TOMOVE New_W = old_W + 𝜕𝐶 𝜕𝑤 New_b = old_b + 𝜕𝐶 𝜕𝑏 Or New_W = old_W + l 𝜕𝐶 𝜕𝑤 ‘l’ is the learning rate that decides how big a step to take towards the minima
  • 28.
    STOCHASTIC GRADIENT DESCENT Insteadof taking the entire training set before performing a move along minima, SGD takes a random set of samples before making a move. Variations 1. Take 1 training sample at a time 2. Batch SGD – take a random set of subsamples
  • 29.
    BACKPROPAGATION i j k wij wjk Input Layer Hidden Layer OutputLayer yt xs i – node in input layer j – node in hidden layer k – node in output layer wij – weight between nodes ‘i’ and ‘j’ wjk – weight between nodes ‘j’ and ‘k’ X – input vector xs – input value of input unit ‘s’ yk – predicted output of output unit ‘k’ ok – actual output of output unit ‘k’ hj – output of hidden unit ‘j’ Errk = ok(1-ok)(yk-ok) Errj = hj(1- hj) 𝑘 𝐸𝑟𝑟𝑘 𝑤𝑗𝑘 𝑤𝑖𝑗 = 𝑤𝑖𝑗 + (𝑙)𝐸𝑟𝑟𝑗 𝑜𝑖 Weight Updation - Do the same for bias also
  • 30.
    TYPES OF NEURALNETWORKS Feed forward network  Information goes only in one direction Single layer perceptron  information goes from input  output  Only 1 output layer  Nodes in output layer are processing elements – with activation function Multilayer perceptron(MLP)  Multiple layers of nodes in a directed graph  Can distinguish non-linearly separable data  Nodes in hidden and output layers – processing elements – with nonlinear activation functions  Input  hidden  output
  • 31.
    COMMON DEEP LEARNING NETWORKSWITH APPLICATIONS Extract patterns from unlabeled data  Restricted Boltzmann Machine  Autoencoder Classification from labelled data  Recurrent neural net  Recursive neural tensor network Image recognition  Deep belief network  Convolutional neural network Object recognition  Convolutional neural network  Recursive neural tensor network Speech Recognition/Time series analysis  Recurrent neural net
  • 32.
  • 33.
    IMAGE CLASSIFICATION –A SIMPLE EXAMPLE Initial use case – image classification Images – denoted by pixels 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 What we see What the computer sees
  • 34.
    DETECT Apply filter/kernel/feature detector ReceptiveField : size of filter in input image Perform element-wise multiplication of filter and receptive field(blue) and add result 0 1 1 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 apply 0 1 1 0 0 1 0 1 1 as 0*0 1*1 1*1 0 0 0*0 0*0 1*1 0 0 0*0 1*1 1*1 0 0 0 0 1 0 0 0 1 1 0 0 Result = 5
  • 35.
    0 1 10 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 5 2 0 ? 2 0 5 2 0
  • 36.
    0 1 10 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 5 2 0 3 2 0 5 2 0 Locations with value = sum of the values in kernel perfectly match the given image
  • 37.
    0 1 10 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 Stride : 1 Move 1 column to right at each step STRIDE 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 Stride : 2 Move 2 columns to right at each step
  • 38.
    ZERO PADDING Size ofoutput = 3x3 If the input matrix is a 10x10 matrix then the output matrix size = ?
  • 39.
    ZERO PADDING Size ofoutput = 3x3 If the input matrix is a 10x10 matrix then the output matrix size = 7x7 What if Size of output matrix should be equal to the size of the input matrix? The actual first element should be at the middle when the filter is first applied. So pad top, left etc with ‘0’, such that filter can be applied with every actual element
  • 40.
    0 0 00 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 Row2, Col1Row3, Col1 Row4, Col1 Row5, Col1
  • 41.
    WHAT’S ALL THISGOT TO DO WITH CNN? Matrix after applying filter on different receptive fields = convolved matrix Also called activation map/feature map In our example is the feature map when 9 filters are applied. Or example is analogous to the working of convolution layer. Input to convolution layer : image Output : Value after applying filter 5 2 0 3 2 0 5 2 0
  • 42.
    BUT… Deep learning doesnot require the programmer to provide the feature – i.e. in our case – the filter So - the filter needs to be learnt by the neural network model and not given as input
  • 43.
    Hidden Nodes Convolution Layer Inputnodes If the image size is 5x5 There are 25 input neurons Receptive Field Results in local connections w1 w 2 w 3 w1 w 2 w 3 w1 w 2 w 3 w1 w 2 w 3 Feature Map Filter : w1, w2, w3 Training Phase : The weights are learnt using backpropagation Activation Function(non-linear) : ReLu or tanh Output of conv layer – given as input to activation function …
  • 44.
    5 2 0 32 0 5 2 0 MAX POOLING Max pool with 2x2 filter and stride 1 i.e take max of every 2x2 filter 5 2 5 2 This results in downsampling and detecting more abstract features While the filter in the conv layer might detect edges This layer may detect more abstract things like objects 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 It has actually found the similarity between the upper and lower portions of the image
  • 45.
    w1 w 2 w 3 w1 w 2 w 3 w1w 2 w 3 w1 w 2 w 3 w4 w5 w4 w5 Input Layer Convolution Layer Max pooling Layer This layer may or may not be present in a CNN Average pooling is also considered But max pooling found to give better results empirically … …
  • 46.
    A PARTIAL CNNWITH MANY HIDDEN LAYERS Has multiple hidden layers of convolution layers and max pooling layers Different filters applied in different layers Example Partial CNN Input Conv layer Conv layer Max pooling Conv layer Conv layer Max pooling …
  • 47.
    FULLY CONNECTED LAYER Lastlayer Neurons in this layer are fully connected to all neurons in the previous layer They can have different weights and bias as normal ANN The weights are multiplied with the output of the previous layer and bias is added – which is input to the activation function
  • 48.
    OUTPUT Usually multiple neurons– based on the number of classes - each outputs probability with which a class occurs If differentiate horse or not 2 output neurons – with probability with which the image is/is not a horse Input Conv layer Conv layer Max pooling Conv layer Conv layer Max pooling Fully connected layer
  • 49.
  • 50.
    AUTOENCODER Unsupervised learning technique Usesbackpropagation Tries to give output that is very similar to the input x1 x2 x3 x'1 x'2 x'3
  • 51.
    RESTRICTED BOLTZMANN MACHINE Shallow 2layer net Connections  Fully connected  Every node in visible layer connected to every node in hidden layer  Undirected  Restricted – no connection between nodes in a layer Training : Uses contrastive divergence or approximate gradient descent
  • 52.
  • 53.
    DATA – TO– VISIBLE UNIT User 1: (MI= 1, F&F = 1, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). User 2: (MI = 1, F&F = 0, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). User 3: (MI = 1, F&F = 1, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). User 4: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). User 5: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). User 6: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). User 1 User 2 User 3 User 4 User 5 User 5 Type 1 Type 2
  • 54.
    HIDDEN UNIT –TYPE OF MOVIE INTERESTED IN • User 1: (MI = 1, F&F = 1, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). Likes action movies • User 2: (MI = 1, F&F = 0, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). Prefers action movies, but doesn’t like F&F. • User 3: (MI = 1, F&F = 1, Die Hard = 1, Italian = 0, Oceans = 0, Bank Job = 0). Likes action movies. • User 4: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). Generally likes heist movies. • User 5: (MI = 0, F&F = 0, Die Hard = 1, Italian = 1, Oceans = 1, Bank Job = 0). Generally likes heist movies. • User 6: (MI = 0, F&F = 0, Die Hard = 0, Italian = 1, Oceans = 1, Bank Job = 1). Likes heist movies. Based on the type liked the corresponding hidden unit is activated more
  • 55.
  • 56.
    RECURRENT NEURAL NET Usedwhen input seen as a sequence of data rather than as a bag of elements Activation Function : tanh or ReLu Learning weights : Back Propagation Through Time(BPTT) Problem : Vanishing Gradient, Exploding Gradient Solutions : Long Short Term Memory(LSTM), Gated Recurrent Units(GRU) Applications : NLP, Machine Translation, Speech Recognition
  • 57.
    RECURRENT NEURAL NET Hasfeedback loop Tries to store previous states in memory – but not able to retain long term information W U V W St-1 yt-1 xt-1 U V W St yt xt U V W St-1 yt+1 xt+1 U V W S y x
  • 58.
    PARAMETERS IN THENETWORK xt – input at time unit ‘t’ st – hidden state at time unit ‘t’ - input to st is (u.xt +w. st-1) which is passed through activation function s-1 = all zeros – initially yt – output at time unit ‘t’ = softmax(v.st)
  • 59.
    RECURSIVE NEURAL TENSOR NET Analyze datawith hierarchical structure Binary tree construction Vector representation – given as input to leaves Application : NLP S N Teena VP V went NP D to N school
  • 60.
  • 61.
  • 62.
    TO ACCESS THEPPT https://www.slideshare.net/lovelynrose/deep-learning-simplified

Editor's Notes

  • #4 QuickStarter has created an outline to help you get started on your presentation. Some slides include information here in the notes to provide additional topics for you to research. More key facts: Academic conference: NIPS 2015, ICML 2016, AAAI 2016, CVPR 2016, ICASSP 2016, ACL 2016, ECCV 2016, Interspeech 2015, ICPR 2016, IJCAI 2016, ICCV 2015, IJCNN 2015, ICRA 2016, EMNLP 2015, WWW 2016, ICIP 2015, SIGIR 2016, UAI 2015, ICDAR 2015, KDD 2016, CHI 2016, NAACL 2016, STOC 2016, CIKM 2015, IEEE CLOUD 2015, COLING 2014, IROS 2015, ICONIP 2015, ICME 2016, ICANN 2014, MICCAI 2015, WSDM 2016, LREC 2016, BMVC 2015, SIGGRAPH 2015, ICDM 2015, ISBI 2016, IEEE SMC 2016, EACL 2014, MM 2015, SLT 2014, AAMAS 2016, ACCV 2014, CP 2015, ISMIR 2015, European Conference on Artificial Intelligence (ECAI) 2016, ICCA 2016, ICCE 2015