Download as PDF, PPTX
Uploaded byIsaac Yowetu
Projectors and Projection Onto a Line
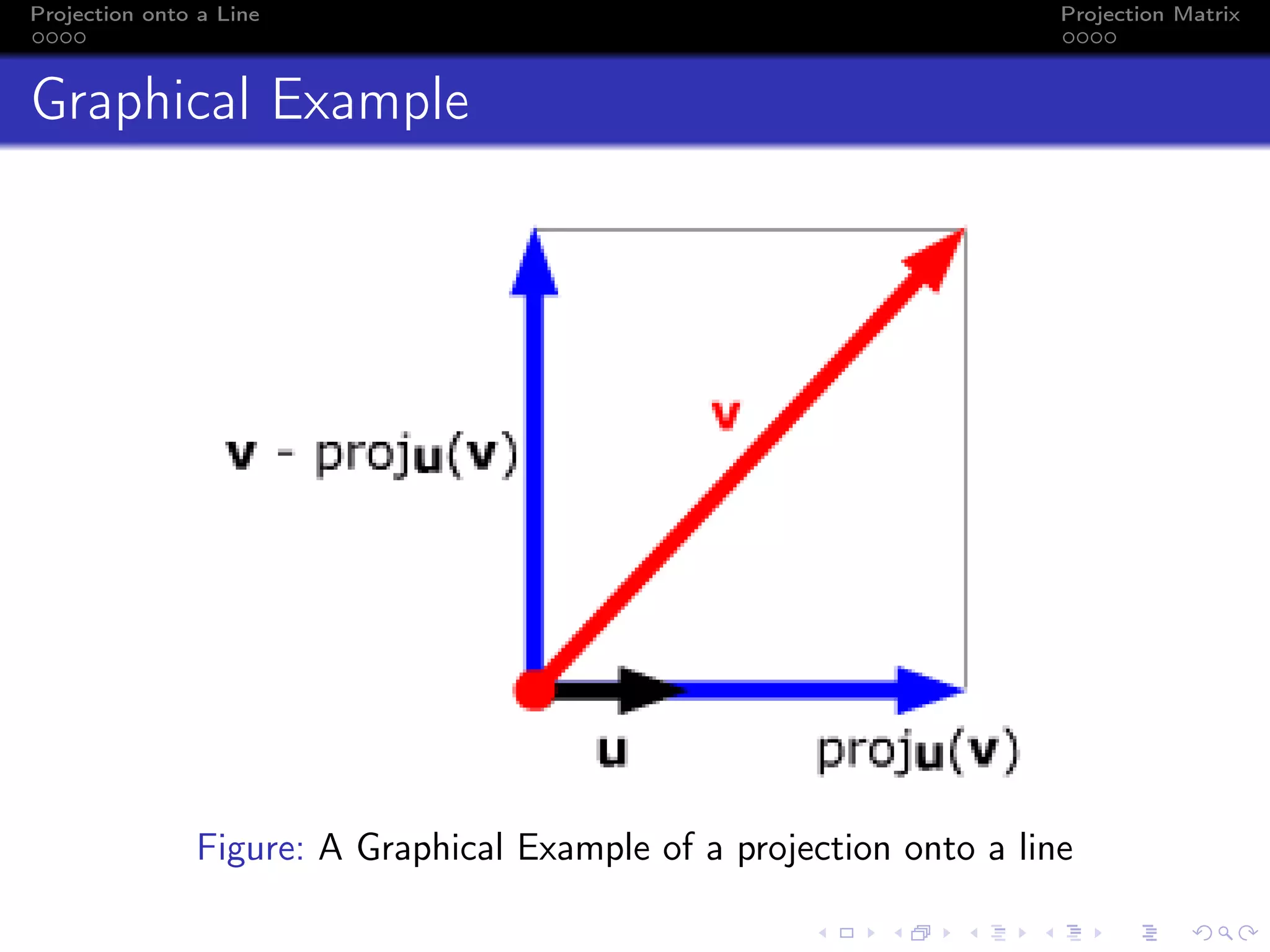
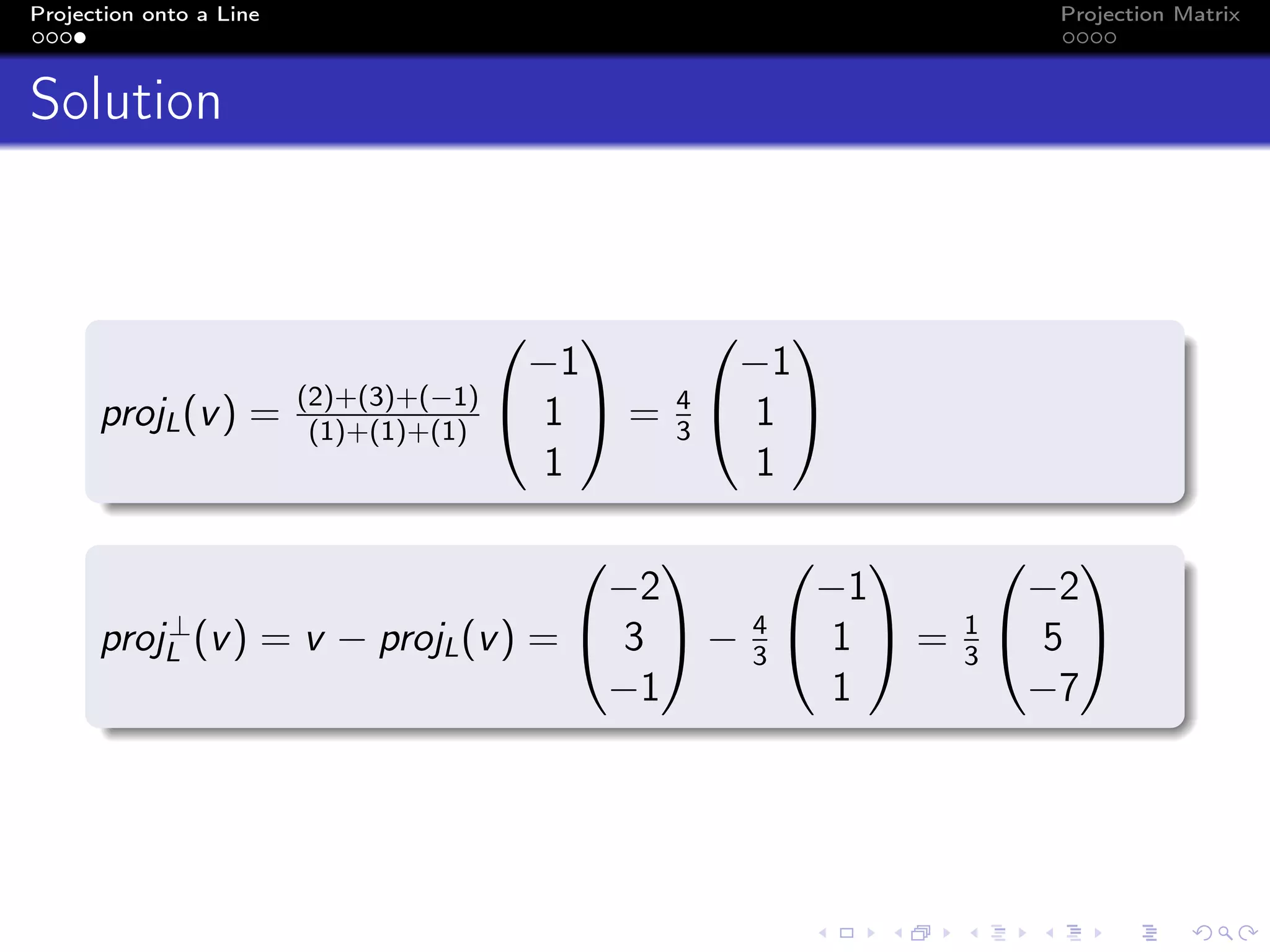
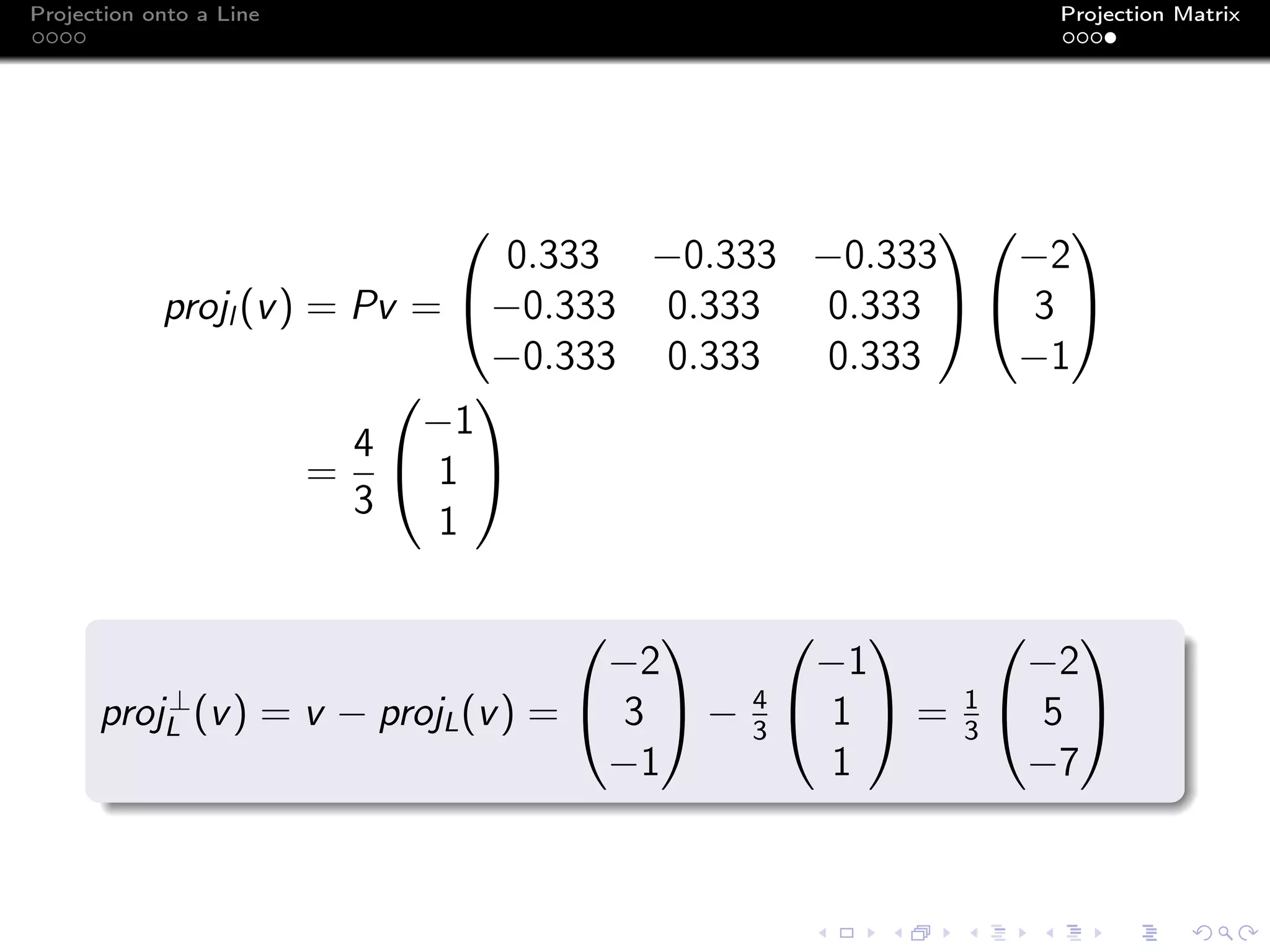
The document discusses the concept of projecting a vector onto a line defined by another vector using projection matrices. It outlines the mathematical formulation for obtaining orthogonal projections and provides examples, including calculations for specific vectors. The document also includes graphical representations and the derivation of the projection matrix.
More Related Content
Similar to Projectors and Projection Onto a Line
![Presentation1 queuing theoory gd[1].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/presentation11-250526203643-8d4ca12a-thumbnail.jpg?width=640&height=640&fit=bounds)
Projectors and Projection Onto a Line
- 1. Projector And ProjectionOnto A Line Numerical Linear Algebra Isaac Amornortey Yowetu NIMS-GHANA July 10, 2020
- 2. Projection onto aLine Projection Matrix Outline 1 Projection onto a Line 2 Projection Matrix
- 3. Projection onto aLine Projection Matrix Graphical Example Figure: A Graphical Example of a projection onto a line
- 4. Projection onto aLine Projection Matrix Orthogonal Projection onto a line Suppose we have L = span{u} is a line and v is projected onto the line u, then ∃c ∈ R s.t: ProjL(v) = c · u v − ProjL(v) = v − c · u We can obtain our orthogonal projection to be (v − ProjL(v)) · (ProjL(v)) = (v − c · u) · (c · u) = 0 (1) v(c · u) − (c · u)(c · u) = 0 (2) (c · u)v = (c · u)(c · u) (3) u · v = c(u · u) (4)
- 5. Projection onto aLine Projection Matrix c = u · v u · u Therefore projL(v) = u · v u · u u
- 6. Projection onto aLine Projection Matrix Example Let v = −2 3 −1 and u = −1 1 1 and let L be the line spanned by u. Compute projL(v) and proj⊥ L (v)
- 7. Projection onto aLine Projection Matrix Solution projL(v) = (2)+(3)+(−1) (1)+(1)+(1) −1 1 1 = 4 3 −1 1 1 proj⊥ L (v) = v − projL(v) = −2 3 −1 − 4 3 −1 1 1 = 1 3 −2 5 −7
- 8. Projection onto aLine Projection Matrix Projection Matrix Here we would like to find a projection matrix P: P = P2 and PT = P P = uuT uT u projL(v) = Pv = uuT uT u v proj⊥ L (v) = v − Pv = v − uuT uT u v
- 9. Projection onto aLine Projection Matrix Example Let v = −2 3 −1 and u = −1 1 1 and let L be the line spanned by u. Compute projL(v) and proj⊥ L (v)
- 10. Projection onto aLine Projection Matrix Solution P = uuT uT u u · uT = −1 1 1 (−1 1 1) = 1 −1 −1 −1 1 1 −1 1 1 uT · u = (−1 1 1) −1 1 1 = 3 ∴ P = 1 3 1 −1 −1 −1 1 1 −1 1 1 = 0.333 −0.333 −0.333 −0.333 0.333 0.333 −0.333 0.333 0.333
- 11. Projection onto aLine Projection Matrix projl (v) = Pv = 0.333 −0.333 −0.333 −0.333 0.333 0.333 −0.333 0.333 0.333 −2 3 −1 = 4 3 −1 1 1 proj⊥ L (v) = v − projL(v) = −2 3 −1 − 4 3 −1 1 1 = 1 3 −2 5 −7