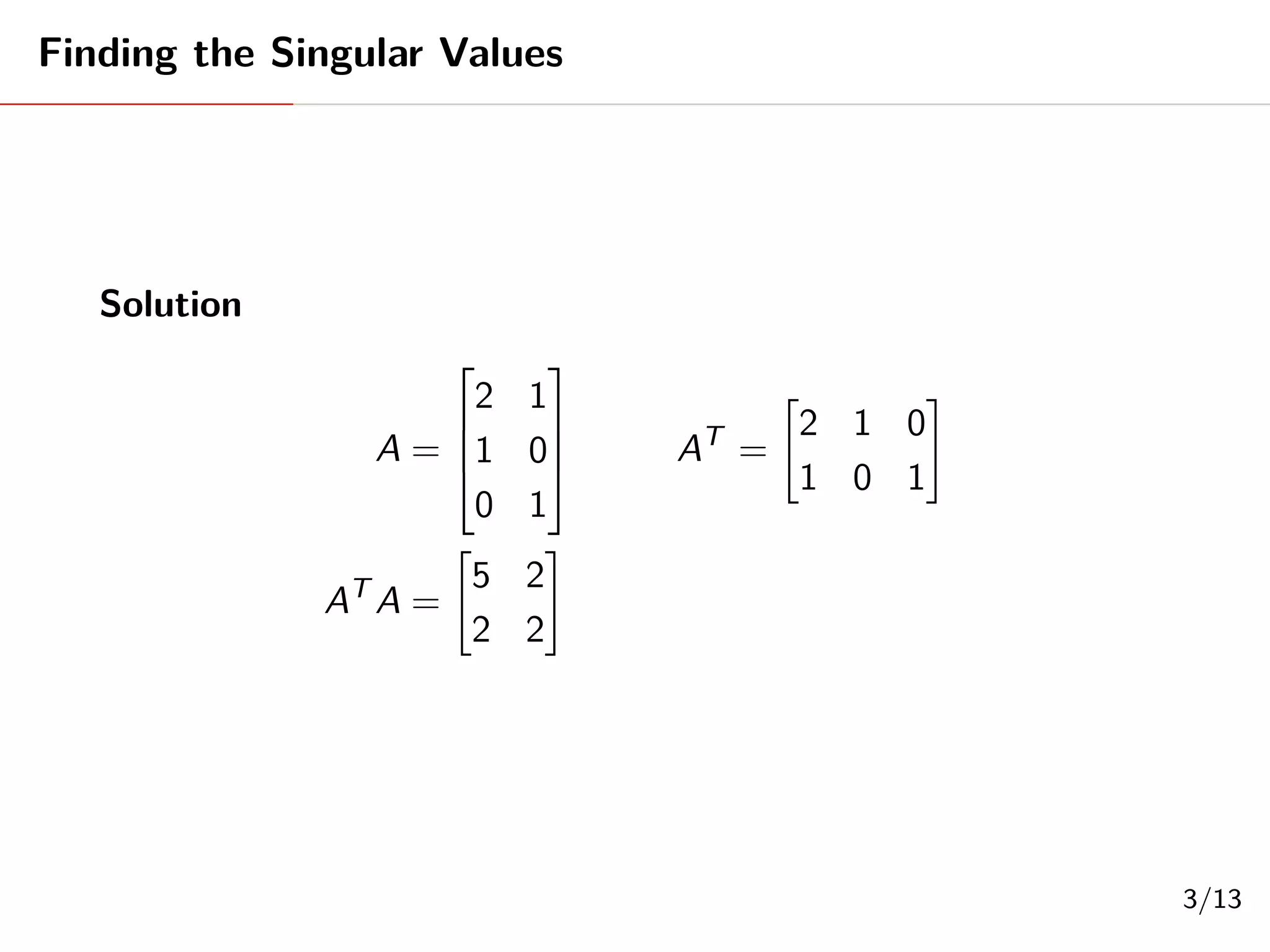
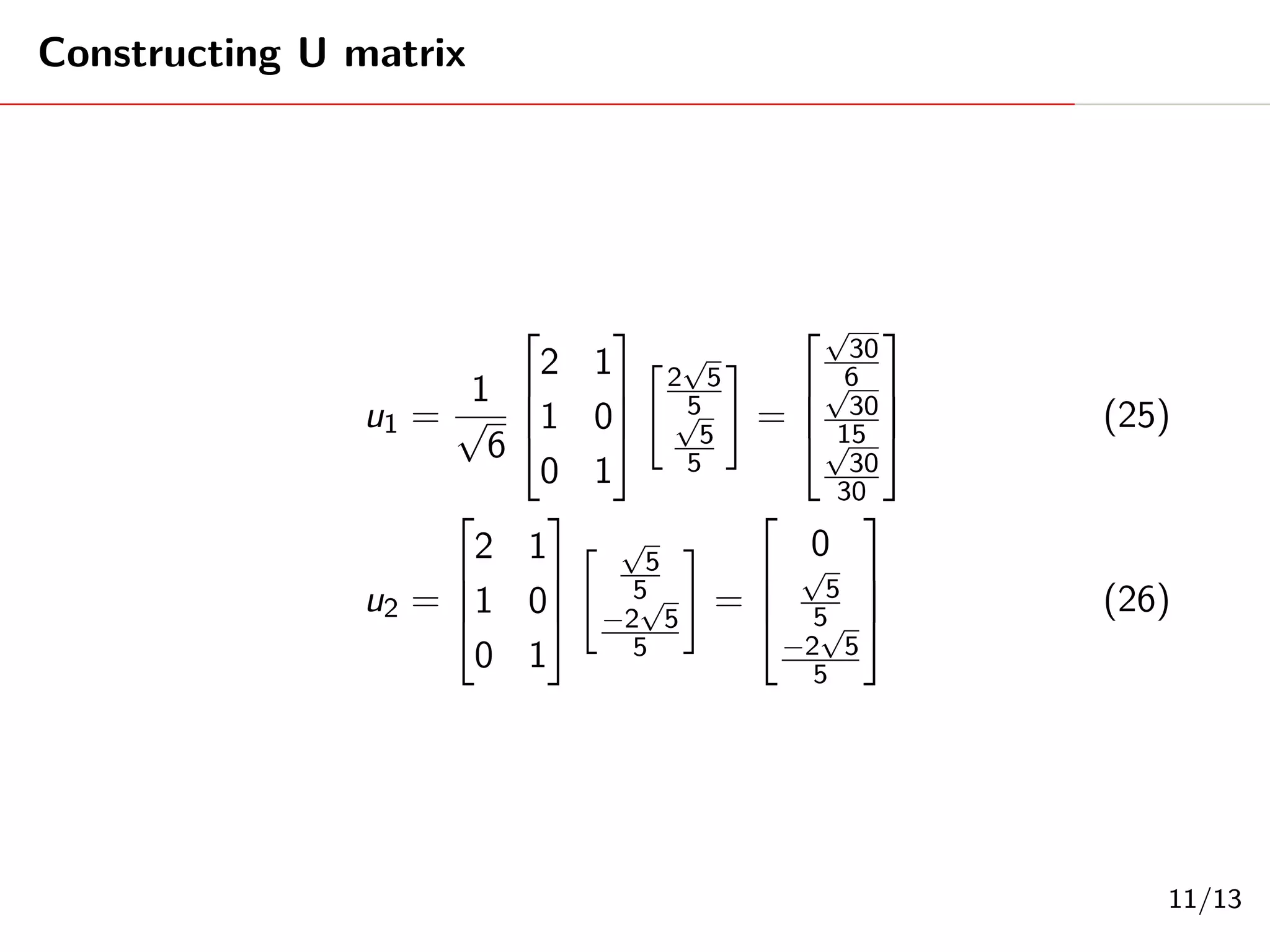
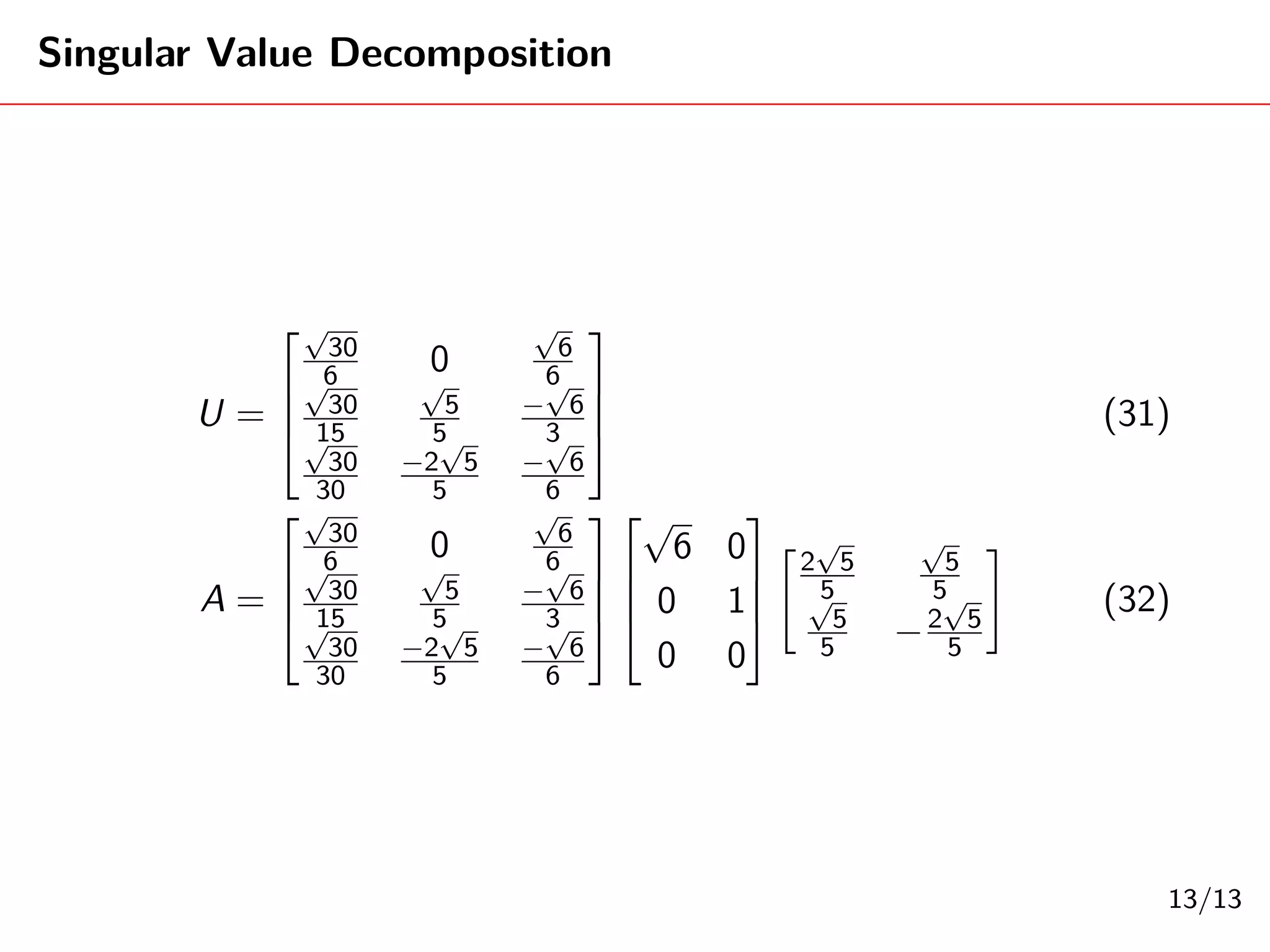
This document provides an example of calculating the singular value decomposition (SVD) of a 3x3 matrix A. It finds the matrices U, Σ, and V such that A = UΣV^T. It first calculates the eigenvalues and eigenvectors of A^TA to construct Σ and V. It then uses A and the eigenvectors to calculate the columns of U. The final SVD of A is presented.

1. Singular Value Decomposition (SVD)
Isaac Amornortey Yowetu
December 31, 2021

2. Example 2
Find the matrices U Σ and V for the matrix
A =




2 1
1 0
0 1




2/13

3. Finding the Singular Values
Solution
A =




2 1
1 0
0 1



 AT
=
"
2 1 0
1 0 1
#
AT
A =
"
5 2
2 2
#
3/13

4. Characteristics Polynomial
det(AT
A) =

9. 5 − λ 2
2 2 − λ

14. (1)
P(AT
A) = (5 − λ)(2 − λ) − 4 (2)
= λ2
− 7λ + 6 (3)
= (λ − 6)(λ − 1) (4)
Eigenvalues
λ1 = σ2
1 = 6 (5)
λ2 = σ2
2 = 1 (6)
4/13

15. Singular Values
σ1 =
p
λ1 =
√
6 (7)
σ2 =
p
λ2 = 1 (8)
Singular Values Decompostion of A
Σ =




√
6 0
0 1
0 0




5/13

16. Constructing Matrix V
A = UΣV T
(9)
AT
A = (UΣV T
)T
UΣV T
(10)
= V ΣT
UT
UΣV T
(11)
= V Σ2
V T
(12)
= VDV T
(13)
AT
A =
"
5 2
2 2
#
(14)
6/13

17. Constructing Matrix V Cont’d
When λ = 6
"
5 − λ 2
2 2 − λ
#
=
"
−1 2
2 −4
#
(15)
By row reduction form, we have:
"
−1 2
2 −4
#
=>
"
−1 2
0 0
#
(16)
Forming equations with some variables:
−x + 2y = 0 (17)
Our eigenvector becomes: (2, 1)t
7/13

18. Constructing Matrix V Cont’d
When λ = 1
"
5 − λ 2
2 2 − λ
#
=
"
4 2
2 1
#
(18)
By row reduction form, we have:
"
2 1
4 2
#
=>
"
2 1
0 0
#
(19)
Forming equations with some variables:
2x + y = 0 (20)
Our eigenvector becomes: (1, −2)t
8/13

19. Let Z be the egigenvectors of the various eigenvalues.
Z =
"
2 1
1 −2
#
We normalized each column of Z to get V
V =
"
2
√
5
5
√
5
5
√
5
5 −2
√
5
5
#
9/13

20. Constructing U matrix
A = UΣV T
(21)
U = {u1, u2} (22)
u1 =
1
s1
Av1 (23)
u2 =
1
s2
Av2 (24)
10/13

21. Constructing U matrix
u1 =
1
√
6




2 1
1 0
0 1




"
2
√
5
5
√
5
5
#
=




√
30
6
√
30
15
√
30
30



 (25)
u2 =




2 1
1 0
0 1




" √
5
5
−2
√
5
5
#
=




0
√
5
5
−2
√
5
5



 (26)
11/13

22. Find the remaining eigenvector
AT
X = 0 (27)
"
2 1 0
1 0 1
#




x
y
z



 =
"
0
0
#
(28)
Forming equations with the variables:
2x + y = 0 (29)
x + z = 0 (30)
Our eigenvector becomes: (1, −2, −1)t
12/13

23. Singular Value Decomposition
U =




√
30
6 0
√
6
6
√
30
15
√
5
5
−
√
6
3
√
30
30
−2
√
5
5
−
√
6
6



 (31)
A =




√
30
6 0
√
6
6
√
30
15
√
5
5
−
√
6
3
√
30
30
−2
√
5
5
−
√
6
6








√
6 0
0 1
0 0




"
2
√
5
5
√
5
5
√
5
5 −2
√
5
5
#
(32)
13/13