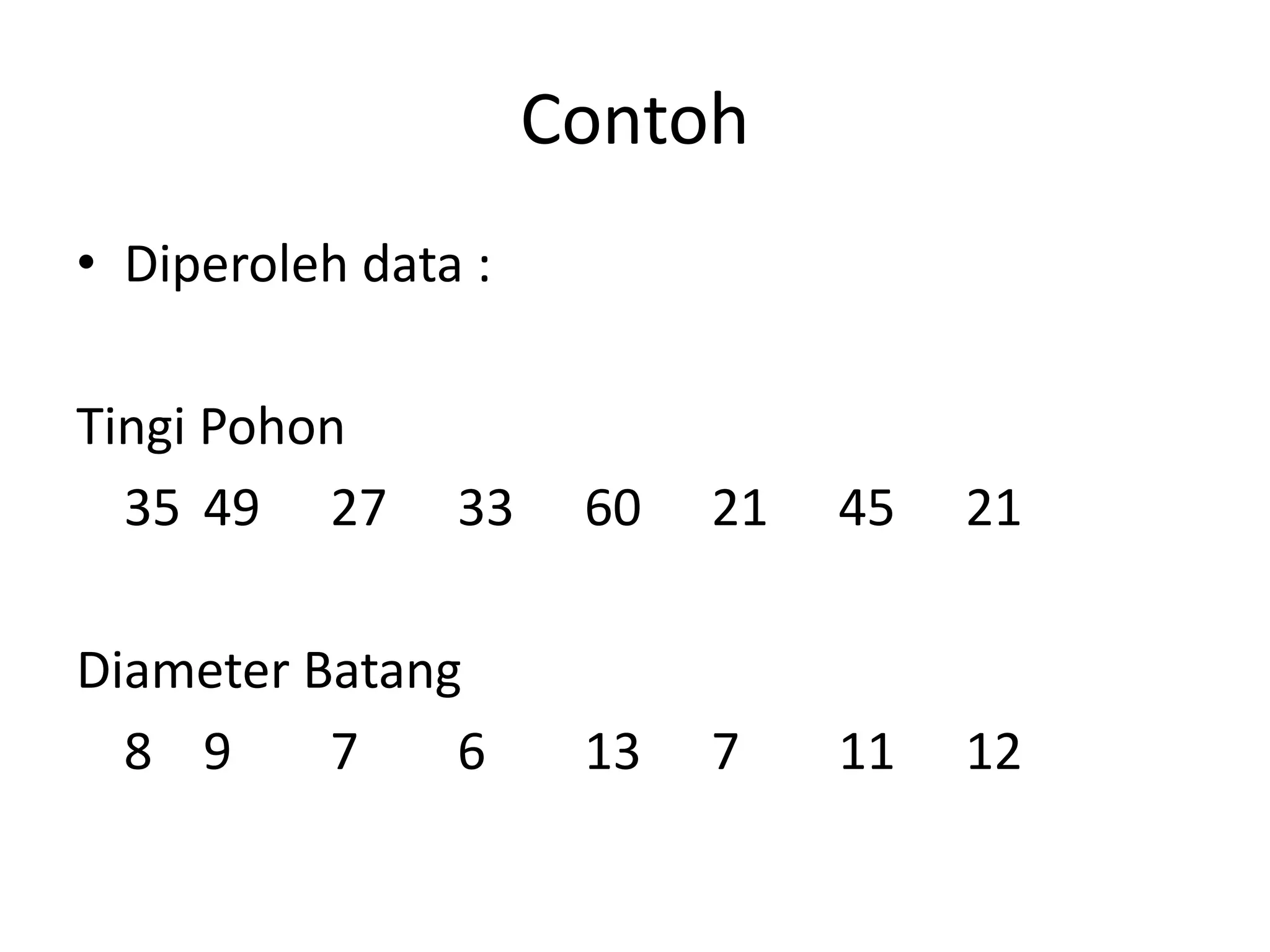
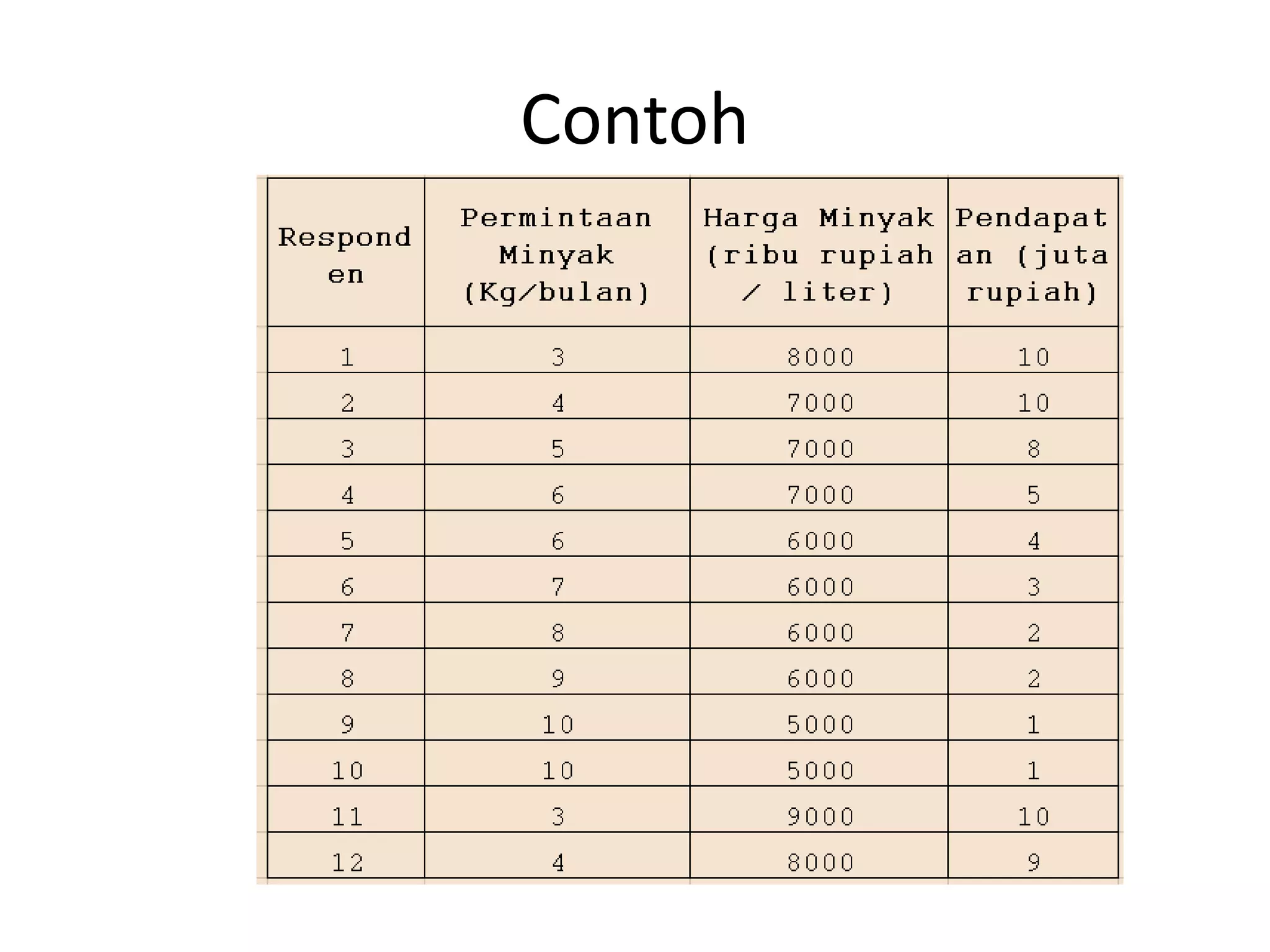
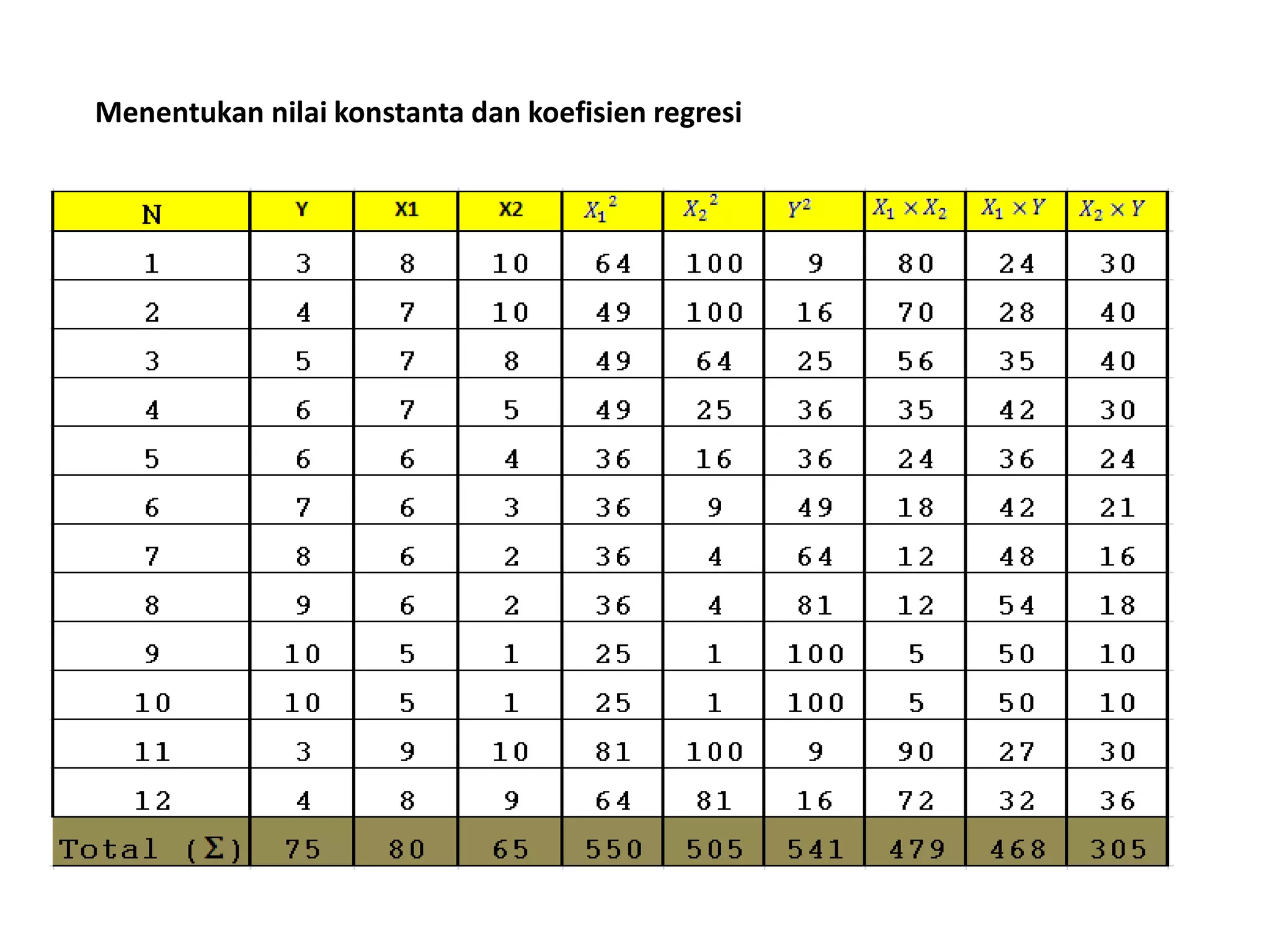
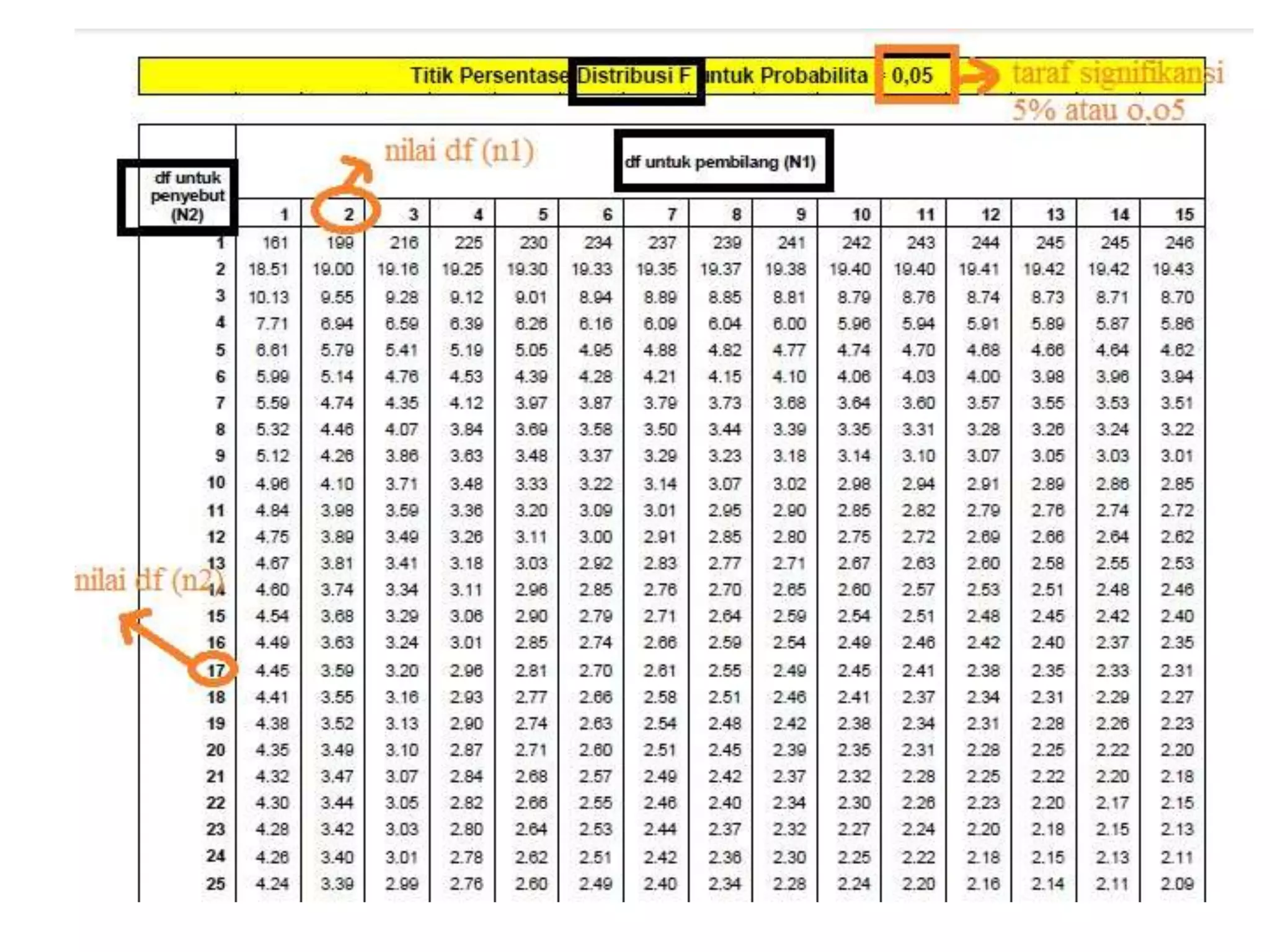
Dokumen tersebut membahas tentang analisis regresi yang digunakan untuk menentukan hubungan antara variabel bebas dan terikat. Regresi linier sederhana menggunakan persamaan Y = a + bX, sedangkan regresi linier berganda menggunakan persamaan Y' = a + b1X1+ b2X2+.....+ bnXn. Langkah-langkah penyelesaian regresi linier berganda dijelaskan beserta contoh soalnya.

1. REGRESI
Agus Purnomo

2. Pengertian
• Analisis regresi dalam statistika adalah salah satu
metode untuk menentukan hubungan sebab-
akibat antara satu variabel dengan variabel(-
variabel) yang lain.
• Analisis regresi dipakai secara luas untuk
melakukan prediksi dan ramalan,
• Analisis ini juga digunakan untuk memahami
variabel bebas mana saja yang berhubungan
dengan variabel terikat, variabel yang paling
dominan, dan untuk mengetahui bentuk-bentuk
hubungan tersebut.

3. Perbedaan Regresi dan Korelasi
• Korelasi adalah suatu teknik analisis statistik untuk
mengetahui hubungan suatu variabel dengan variabel
lainnya.
• Regresi adalah suatu analisis yang digunakan untuk
mengetahui pengaruh dari suatu variabel dengan
variabel lainnya. Hasil dari analisis regresi adalah suatu
persamaan regresi yang merupakan fungsi prediksi
atau peramalan suatu variabel dengan menggunakan
variabel yang lain. Dengan analisis ini, kita dapat
memprediksi perilaku dari variabel dependen dengan
menggunakan data variabel independen.

4. Regresi Linier Sederhana
Y = a + bX
Dimana :
Y = Variabel Dependent
X = Variabel Independent
a = konstanta
b = koefisien regresi
a = (Σy) (Σx²) – (Σx) (Σxy)
. n(Σx²) – (Σx)²
b = n(Σxy) – (Σx) (Σy)
. n(Σx²) – (Σx)²

5. Contoh
• Diperoleh data :
Tingi Pohon
35 49 27 33 60 21 45 21
Diameter Batang
8 9 7 6 13 7 11 12

6. Rgresi Linier Berganda
Y’ = a + b1X1+ b2X2+…..+ bnXn
Keterangan:
Y’ = Variabel dependen (nilai yang
diprediksikan)
X1 dan X2 = Variabel independen
a = Konstanta
b = Koefisien regresi

7. Dalam menentukan nilai ‘a’ dan ‘b1′,’b2′,’b3’,..,
digunakan persamaan regresi linier berganda:
1. SY = an+b1SX1++b2SX2+b3SX3+…
2. SX1Y = aSX1+b1SX1²+b2SX1X2+…
3. SX2Y = aSX2+b2SX1X2+b2SX21²+… dan
seterusnya.
Untuk menghitung nilai ‘a’,’b1′,’b2′,’b3′,… pada
persamaan regresi linier berganda dapat
dirumuskan =nx-1 di mana nx = banyaknya
variabel bebas (X).

8. Contoh

9. Langkah Penyelesaian
Langkah-langkah penyelesaiannya:
Variabel bebas dan variabel tak bebas
Variabel Bebas : X1 = Harga minyak goreng dan
X2 = Pendapatan konsumen
Variabel Tak Bebas : Y = Permintaan minyak
goreng
> Persamaan regresi linear berganda :
Y' = a + b1X1 + b2X2

10. Menentukan nilai konstanta dan koefisien regresi

12. Khusus untuk parameter b1 data adalah dalam ribuan, sehingga hasil tersebut harus
dibagi dengan 1000, diperoleh b1 = -0,000582 = -0,001.
Jadi persamaan Regresi Linear Berganda dengan dua variabel bebas adalah :
Y' = 12,7753 - 0,001 X1 - 0,488 X2
Interpretasi koefisien regresi
Nilai a = 12,7753 artinya jika tidak ada harga minyak goreng dan pendapatan
konsumen, namun permintaan akan minyak goreng sebanyak 12,7753.
Nilai b1 = -0,001 artinya jika harga minyak goreng meningkat satu rupiah maka akan
terjadi penurunan permintaan sebesar 0,001 satuan dimana pendapatan konsumen
dianggap tetap.
Nilai b2 = - 0,488 artinya jika pendapatan konsumen mengalami kenaikan sebesar
satu rupiah maka akan terjadi penurunan permintaan gula sebesar 0,488 satuan
dimana harga gula dianggap tetap.

13. Menghitung Koefisien Korelasi Berganda

16. Pengujian Hipotesis
Tabel F =
Df1 = K -1
Df2 = n – k
K = jumlah variabel