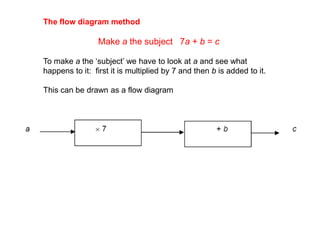
This document discusses three methods for rearranging or transposing formulae: the balance method, flow diagram method, and cross method. The balance method treats an equation like a balance scale and allows operations on one side as long as the same operations are applied to the other. The flow diagram method draws a diagram to visualize the operations on a variable and then reverses the operations to isolate the variable. The cross method takes terms over the equal sign and changes their operations from addition to subtraction and vice versa. Examples are provided for making the variable a the subject using each method.

1. Rearranging or transposing formulaeBTEOTSSSBAT:

2. Write down the integers which satisfy the following:0 < x < 31 < x < 5-1 < x < 2-1 < x 2-1 < x 2

3. Key termsEquationExpressionFormulaRearrangeTransposeSubjectBalanceFlow diagram

4. There are different ways of doing this:balance method

5. flow diagram method

6. cross methodLook at the examples to find which method you think is the best and then use whichever method you are happiest with.

7. The balance method We can think of an equation as a balance. We can do whatever we want to one side, provided we do the same to the other side.

8. 7a + b = c 7a + b (- b) = c (- b)7a = c – b Cancelling the 7s on the LHS gives: which gives us our answer!

9. The flow diagram method Make a the subject 7a + b = c To make a the ‘subject’ we have to look at a and see what happens to it: first it is multiplied by 7 and then b is added to it. This can be drawn as a flow diagram

10. To rewrite the expression as a = … we can reverse the diagram and do the ‘inverse’ (opposite) operations: Reading from the right to left we have: c subtract b divided by 7 This can then be written in mathematical language as: a = c – b 7

11. Cross methodIn the cross method, every time we take something over the equals symbol we ‘reverse’ its operation (+ becomes -, - becomes +;  becomes , and  becomes  etc.)Example: Make a the subject of 7a + b = cSo 7a + b = c take the b over and change its sign to become – b7a = c - btake the 7 over and change its sign to become  77a = c - ba = c - bthis then gives us our answer 7