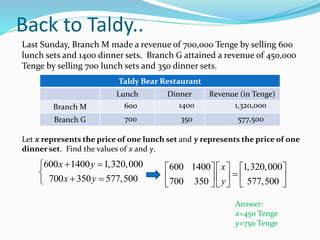
This document provides learning objectives and examples for representing systems of linear equations in matrix form. It defines matrix form, shows how to write 2x2 systems of equations in matrix form as AX = B, and explains how to find the inverse of a 2x2 matrix A-1 to solve the system. An example problem at the end represents a real-world scenario about revenue at two restaurant branches in matrix form to solve for the price of lunch and dinner sets.

1. December 12, 2013

2. Learning Objectives
 To define matrix form
 To name the elements of matrix form
 To represent a 2x2 system of linear equations in matrix
form
 To calculate the determinant of A, det(A)
 To calculate the inverse of A, i.e. A
1 , if det(A)≠0
 To solve the 2x2 system of linear equations by using
inverse matrix method

3. Consider this..
Taldy Bear Restaurant has 2 branches. Branch M is located in a mall and
Branch G is located nearby a gym. Both branches sell lunch and dinner
sets to public everyday.
Last Sunday, Branch M made a revenue of 700,000 Tenge by selling 600
lunch sets and 1400 dinner sets. Branch G attained a revenue of 450,000
Tenge by selling 700 lunch sets and 350 dinner sets.
1. Fill in the blanks in the table below.
Taldy Bear Restaurant
Lunch Dinner Revenue (in Tenge)
600 1400 1,320,000
Branch M
Branch G 700 350 577,500
2. Let x represents the price of one lunch set and y represents the price of
one dinner set. Set up 2x2 system of equations that represents the above
information
x y
x y
  
  
600 1400 1,320,000
700 350 577,500

4. Matrix Form
 Any 2x2 system of linear equations can be written in
matrix form.
 Example:
x y
x y
  
  
2 7
3 4 17
a 2x2 system of linear
equations
x
y
1 2 7
3 4 17
     
      
     
Matrix form:
Coefficient
matrix
unknowns constants
AX  B

5. Give it a try
Express each of the following systems of equations in
matrix form
x y
x y
  
  
3 5 13
2 7 81
x y
x y
   
  
3 4 6
3 4 18
x
y
 3  5     13

      
 2 7     81

x
y
 3  4     6

      
 3 4     18


6. Inverse of 2x2 Matrix
 Suppose A is a 2x2 matrix. The inverse of a 2x2
matrix A, denoted by , is a 2x2 matrix such that
 Hence,
 
 
 



 
 If , then
1 A
1 1 AA A A I    

1 1 d b
   
  
A
ad bc c a
  
a b
A
c d
Determinant of
matrix A
Note:
If the determinant of
matrix is zero, then
doesn’t exist.
1 A
1 1
1
AX B
A AX A B
X A B
Matrix Form
Solution of the system
in term of A-1

7. Practice makes perfect
1. Which one of the following matrices does not have an inverse?
1 2 1 2 1 2
     
  ,   ,
 
 3  5   3 4   3 6

2. Express the system of equations in matrix form.
Determinant
(1)(6)-(3)(2)=0
x y
x y
  
  
2 7
3 4 17
Answer: (3,2)
Find the inverse of the coefficient matrix. Solve the system for x and y.
3. Express the system of equations in matrix form.
x y
x y
  
  
5 13
3 2 5
Answer: (3,-2)
Find the inverse of the coefficient matrix. Solve the system for x and y.

8. Back to Taldy..
Last Sunday, Branch M made a revenue of 700,000 Tenge by selling 600
lunch sets and 1400 dinner sets. Branch G attained a revenue of 450,000
Tenge by selling 700 lunch sets and 350 dinner sets.
Taldy Bear Restaurant
Lunch Dinner Revenue (in Tenge)
600 1400 1,320,000
Branch M
Branch G 700 350 577,500
Let x represents the price of one lunch set and y represents the price of one
dinner set. Find the values of x and y.
x y
x y
  
  
600 1400 1,320,000
700 350 577,500
x
y
600 1400 1,320,000
700 350 577,500
     
      
     
Answer:
x=450 Tenge
y=750 Tenge