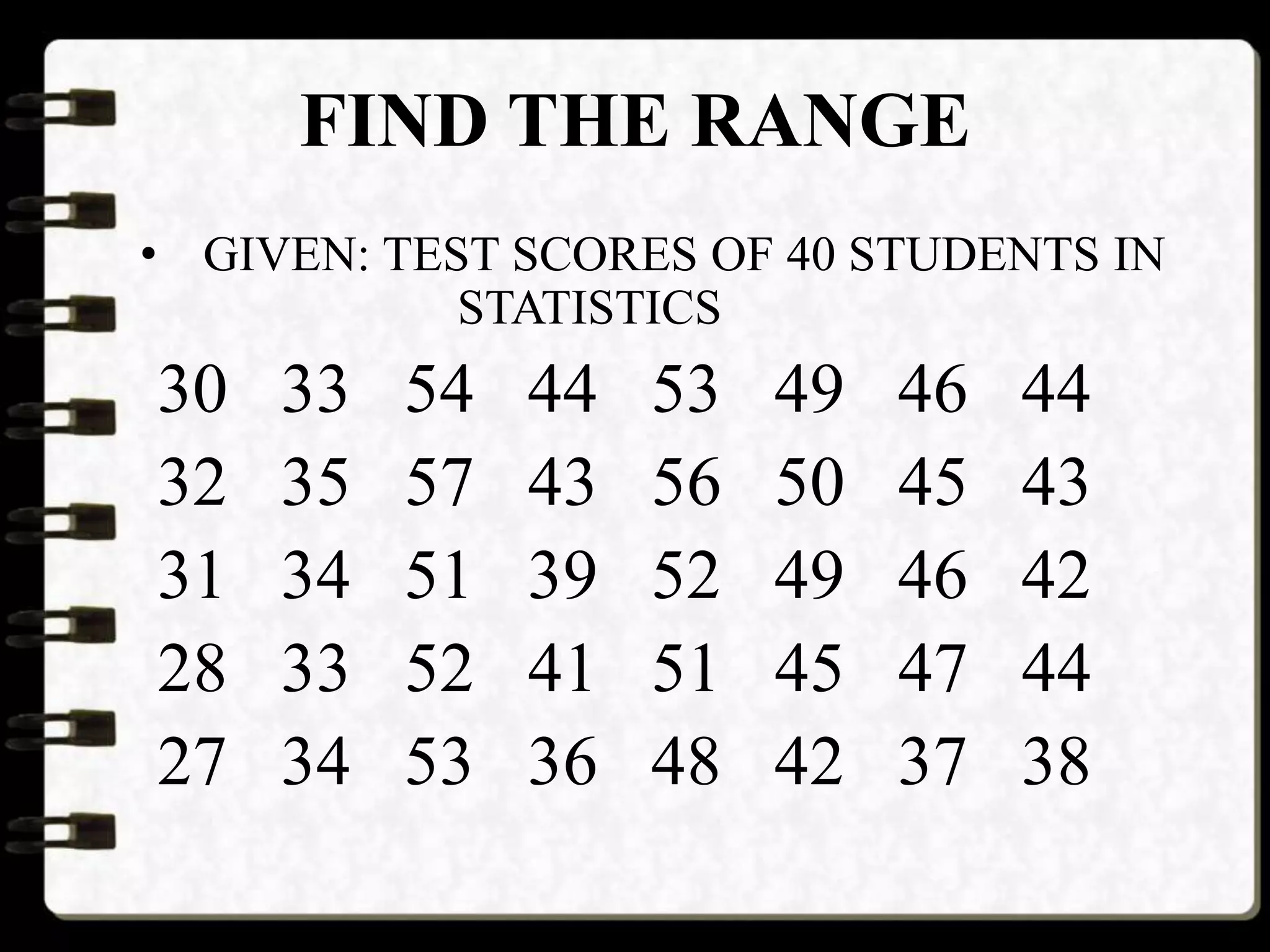
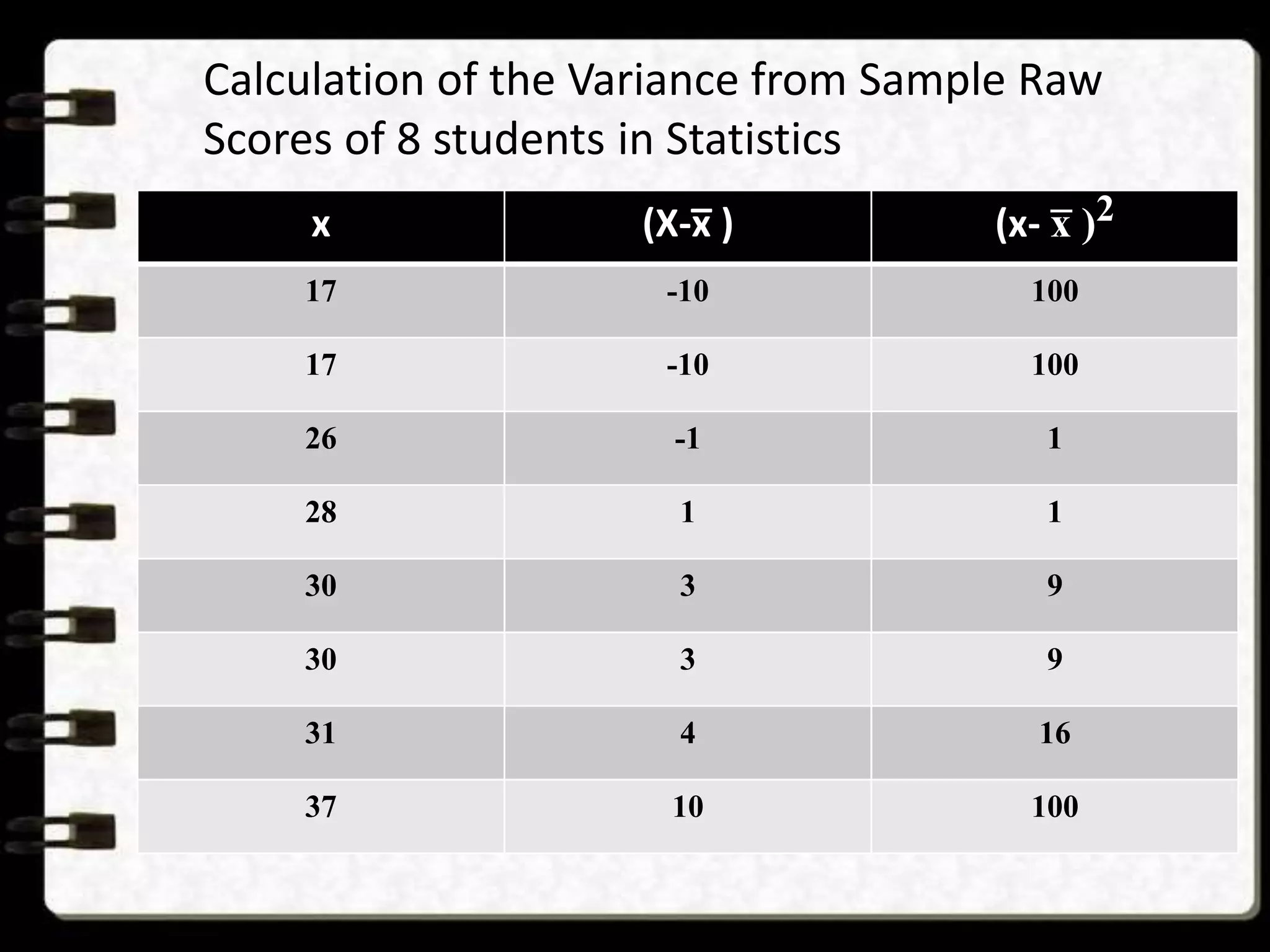
1) The range, interquartile range, average deviation, variance, and standard deviation are common measures used to describe the distribution and variability of data. 2) The range is the difference between the greatest and least values in a data set. The interquartile range describes variability by looking at the spread between the first and third quartiles. 3) Variance and standard deviation both consider how far each observation is from the mean, with variance being the average of the squared deviations and standard deviation being the square root of the variance.

2. Measures
of
Variation
BY: JERLY TANODRA
JHONNA BARROSA
MARY GRACE PARADIANG

3. Measures of variation
-Measures of variation
are used to describe the
distribution of the data.

4. Range
-The range is the difference
between the greatest and least
data values.
FORMULA:
R= H-L

5. FIND THE RANGE
• GIVEN: TEST SCORES OF 40 STUDENTS IN
STATISTICS
30 33 54 44 53 49 46 44
32 35 57 43 56 50 45 43
31 34 51 39 52 49 46 42
28 33 52 41 51 45 47 44
27 34 53 36 48 42 37 38

6. STEPS IN FINDING THE RANGE
1. Arrange the data/number from least
value to greatest value.
EXAMPLE:
27,28,30,31,32,33,33,34,34,35,36,37,38,39,41,4
2,42,43,43,44,44,44,45,45,46,46,47,48,49,49,50
,51,51,52, 52,53,53,54,56,5757

7. STEPS IN FINDING THE RANGE
2. Find the RANGE
FORMULA:
R= H-L
SOLUTION:
R= 57- 27
= 30

8. INTERQUARTILE
• The interquartile range (IQR)
is a measure of variability,
based on dividing a data set
into quartiles.

9. QUARTILES
-Quartiles divide a rank-ordered data set into
four equal parts. The values that divide each part are
called the first, second, and third quartiles; and they
are denoted by Q1, Q2, and Q3, respectively.
• Q1 is the "middle" value in the first half of the
rank-ordered data set.
• Q2 is the median value in the set.
• Q3 is the "middle" value in the second half of the
rank-ordered data set.

10. FORMULA
• INTERQUARTILE RANGE
IQR = Q3 - Q1

11. STEPS IN GETTING THE IQR
1: Put the numbers in order.
EXAMPLE:
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.
2: Find the median.
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.

12. STEPS IN GETTING THE IQR
3: Place parentheses around the numbers
above and below the median.
Not necessary statistically, but it makes Q1
and Q3 easier to spot.
(1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27).
4: Find Q1 and Q3
Think of Q1 as a median in the lower half of
the data and think of Q3 as a median for the
upper half of data.
(1, 2, 5, 6, 7), 9, ( 12, 15, 18, 19, 27).
Q1 = 5 and Q3 = 18.

13. STEPS IN GETTING THE IQR
5: Subtract Q1 from Q3 to find
the interquartile range.
18 – 5 = 13.

14. Odd Set of Numbers:
Sample question: Find the IQR for the following data
set: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
Step 1: Put the numbers in order.
3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
Step 2: Make a mark in the center of the
data:
3, 5, 7, 8, 9, | 11, 15, 16, 20, 21.

15. Odd Set of Numbers:
Step 3: Place parentheses around the numbers above
and below the mark you made in Step 2–it makes Q1 and
Q3 easier to spot.
(3, 5, 7, 8, 9), | (11, 15, 16, 20, 21).
Step 4: Find Q1 and Q3
Q1 is the median (the middle) of the lower half of
the data, and Q3 is the median (the middle) of the
upper half of the data.
(3, 5, 7, 8, 9), | (11, 15, 16, 20, 21).
Q1 = 7 and Q3 = 16.

16. Odd Set of Numbers:
Step 5: Subtract Q1 from Q3.
16 – 7 = 9.
This is your IQR.

17. QUARTILE DEVIATION
• The semi interquartile range (SIR)
(also called the quartile deviation) is a
measure of spread. It tells you
something about how data is
dispersed around a central point
(usually the mean). The difference of
Q3−Q1 divided by 22

18. FORMULA

19. STEPS
Example:
Question: Find the Quartile Deviation for the
following set of data:
{490, 540, 590, 600, 620, 650, 680, 770, 830,
840, 890, 900}
Step 1: Find the first quartile, Q1.
This is the median of the lower half of the set
{490, 540, 590, 600, 620, 650}.
Q1 = (590 + 600) / 2 = 595.

20. STEPS
Step 2: Find the third quartile, Q3.
This is the median of the upper half of the set
{680, 770, 830, 840, 890, 900}.
Q3 = (830 + 840) / 2 = 835.
Step 3: Subtract Step 1 from Step 2.
835 – 595 = 240.
Step 4: Divide by 2. 240 / 2 = 120
The quartile deviation for this set of data is 12.

21. AVERAGE DEVIATION
• A measure of absolute
dispersion that is affected by
every individual score.

22. FORMULA FOR AVERAGE
DEVIATION
Σ/x-x̅ /
A.D=
n-1
Where A.D= average
deviation
n = total number of
scores
x = individual scores
x̅ =mean of all scores

23. EXAMPLE:
Calculation of Average
Deviation from Sample Raw scores
of Eight Students in Statistics and 9
students in Psychology

24. STATISTICS PSYCHOLOGY
X /X- x̅ / X /X- x̅ /
17 -10 15 -11.67
17 -10 19 -7.67
26 -1 20 -6.67
28 1 24 -2.67
30 3 28 1.33
30 3 30 3.33
31 4 32 5.33
37 10 32 5.33
216 42 40 13.33
240 57.33

25. • STATISTICS: PSYCHOLOGY:
226 240
x̅ = x̅ =
8 9
x̅ = 27 x̅ = 26.67

26. • AVERAGE DEVIATION:
Σ / X - x̅ /
AD=
n-1
STATISTICS: PSYCHOLOGY:
42 57.33
AD= AD =
8-1 9-1
AD = 6 AD = 7. 17

27. VARIANCE
• The Variance is a measure of
variability that considers the position
of each observation relative to the
mean of the set of scores.

28. Σ( x - x̅ )2
• Sample variance (s2
) =
n-1
• Where: x = individual score
x̅ = mean of the set of score
n = sample size
s2
= variance

29. Calculation of the Variance from Sample Raw
Scores of 8 students in Statistics
x (X-x̅ ) (x- x̅ )2
17 -10 100
17 -10 100
26 -1 1
28 1 1
30 3 9
30 3 9
31 4 16
37 10 100

30. Σ( x - x̅ )2
S2=
n-1
336
S2 =
8-1
S2 = 48

31. STANDARD DEVIATION
• The Standard deviation (SD) is the measure of
variability that measures all the scores in the
distribution rather than through extreme
scores.
• The standard deviation is simply the square
root of the variance.

32. FORMULA FOR SD
Σ( x - x̅ )2
S2=
n- 1
Where: SD = Standard deviation
x = individual scores
x̅ = mean of scores
n = total number of scores

33. Calculation of the Variance from Sample Raw
Scores of 8 students in Statistics
x (X-x̅ ) (x- x̅ )2
17 -10 100
17 -10 100
26 -1 1
28 1 1
30 3 9
30 3 9
31 4 16
37 10 100

34. Σ( x - x̅ )2
SD=
n-1
336
SD =
8-1
SD = 48

35. THE END !!!