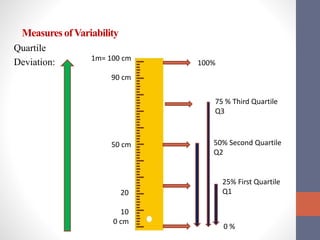
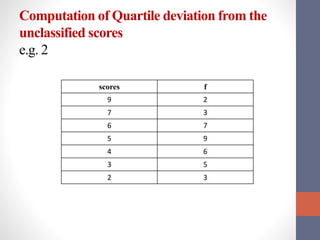
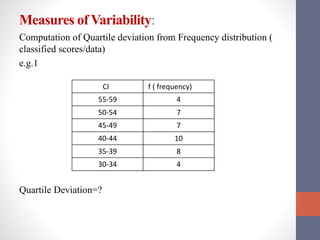
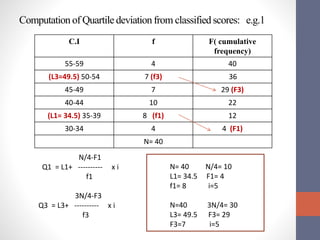
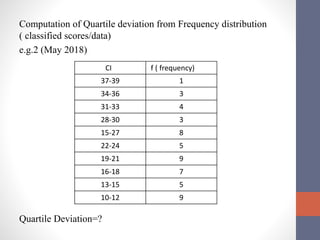
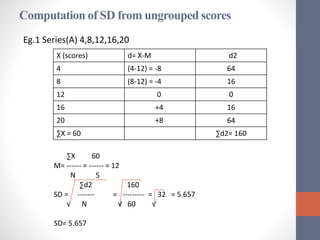
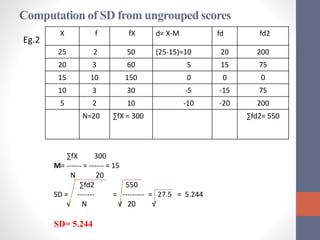
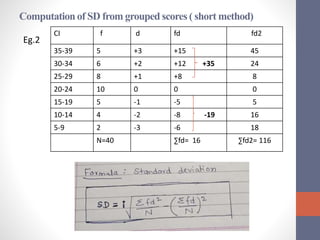
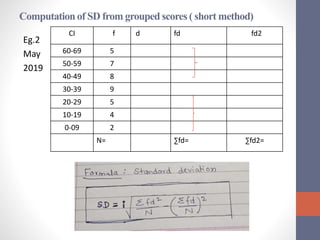
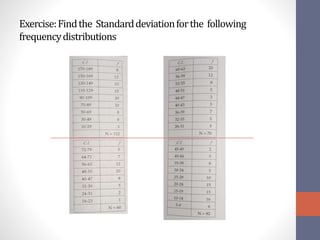
This document discusses measures of variability used to interpret test scores, including quartile deviation and standard deviation. Quartile deviation is calculated by finding the difference between the third quartile (Q3) and first quartile (Q1) and dividing by 2. Standard deviation is the most reliable measure of variability and is calculated by finding the sum of the squared deviations from the mean divided by the total number of values. Examples are provided to demonstrate computing both measures from raw data and frequency distributions.

1. MAEER’s
MIT SaintDnyaneshwarB.Ed.College,
Alandi(Devachi),Pune.
B.Ed. 104
ASSESSMENT AND EVALUATION FOR
LEARNING
Unit 4- INTERPRETING TEST SCORES
(Statistics): (4.2)
By.
Asst.Prof. Gangotri V. Rokade

2. UNIT4 INTERPRETINGTESTSCORES
(1 CREDIT)
Statistical measures to interpret the test scores (Meaning,
Characteristics, and Uses)
4.1 Measures of Central Tendency : Mean, Median, Mode
4.2 Measures of Variability : Quartile Deviation, Standard
Deviation
4.3 Percentile and Percentile Rank
4.4 Co-efficient of correlation by Spearman’s Rank Difference
method
4.5 Standard Scores: Z and T (Concept Only)
4.6 Graphical representation of data : Histogram, Frequency
polygon
4.7 Normal Probability Curve : Properties, Uses
4.8 Skewness and Kurtosis

3. UNIT 4 INTERPRETING TEST SCORES
4.2 Measures of Variability : Quartile Deviation, Standard
Deviation
Variability: Variability is the measure which denotes how far the
scores in the given series are lying from the measures of central
tendency.
According to Lindquist- Variability denotes a limit in which the
scores in a given series deviate below or above the mean.
e.g.
Series A: 5,10,15,20,25,30,35 Mean=20 Median =20
Series B: 1,2,4,20,28,42,43 Mean=20 Median =20

4. 4.2 Measures ofVariability
1. Range (R) √
2. Quartile Deviation (Q)
3. Average Deviation (AD) X
4. Standard Deviation (SD)

5. Measures ofVariability
Quartile
Deviation: 1m= 100 cm
90 cm
50 cm
20
10
0 cm
75 % Third Quartile
Q3
50% Second Quartile
Q2
25% First Quartile
Q1
100%
0 %

6. Definitions:
First Quartile: (Q1)- If the scores in a given series are
arranged in an ascending order then the first quartile is a
point, below which 25% ( ¼ th) of the scores lie.
Second Quartile: (Q2)- If the scores in a given series are
arranged in an ascending order then the second quartile is a
point, below and above which 50% ( ½ ) of the scores lie.
Third Quartile: (Q3)- If the scores in a given series are
arranged in an ascending order then the first quartile is a
point, below which 75% (3/4 th) of the scores lie.
_____________________________________________
Quartile Deviation (Q) formula by Lindquist
Q3 – Q1
Q = ------------------
2

7. Computationof Quartile deviation from unclassifiedscores
E.g. 1: Series: 4,7,4,8,2,10,15,12,14,6,11 find Q.
Ans: Ascending order of series = 2,4,4,6,7,8,10,11,12,14,15
Q3 – Q1
Q = ------------------
2
(N+1) 11+1 12
Q1 = ------------------ = -------- = -------- = 3 rd score = 4
4 4 4
3 (N+1) 3(11+1) 36
Q3 = ------------------ = ------------ = --------- = 9th score = 12
4 4 4
Q3 – Q1 12-4 8
Q = ------------------ = -------------- = --------------- = 4 = Quartile deviation
2 2 2

8. Computation of Quartile deviation from the
unclassified scores
e.g. 2
scores f
9 2
7 3
6 7
5 9
4 6
3 5
2 3

9. Computationof Quartile deviation from the unclassified scores
scores f F
9 2 35
7 3 33
6 7 30 Q3
5 9 23
4 6 14 Q1
3 5 8
2 3 3
N=35
35+1 36
Q1 = -------------- = --------- = 9th score = 4
4 4
3( 35+1) 108
Q3 = -------------- = --------- = 27th score = 6
4 4
6-4 2
Q= -------= ------ = 1
2 2

10. Measures of Variability:
Computation of Quartile deviation from Frequency distribution (
classified scores/data)
e.g.1
Quartile Deviation=?
CI f ( frequency)
55-59 4
50-54 7
45-49 7
40-44 10
35-39 8
30-34 4

11. Computation of Quartile deviationfrom classifiedscores: e.g.1
C.I f F( cumulative
frequency)
55-59 4 40
(L3=49.5) 50-54 7 (f3) 36
45-49 7 29 (F3)
40-44 10 22
(L1= 34.5) 35-39 8 (f1) 12
30-34 4 4 (F1)
N= 40
N/4-F1
Q1 = L1+ ---------- x i
f1
3N/4-F3
Q3 = L3+ ---------- x i
f3
N= 40 N/4= 10
L1= 34.5 F1= 4
f1= 8 i=5
N=40 3N/4= 30
L3= 49.5 F3= 29
F3=7 i=5

12. N/4-F1 10- 4
Q1 = L1+ ---------- x i = 34.5 + -------- x 5
f1 8
30
= 34.5 + -------- = 34.5 + 3.75 = 38.25
8
3N/4-F1 30-29
Q3 = L3+ ------------ x i = 49.5 + -------- x 5
f3 7
5
= 49.5 + -------- = 49.5 + 0.714 = 50.214
7
Q3 – Q1 50.214 - 38.25
Q = ------------------ = ------------------------- = 5.982
2 2

13. Computation of Quartile deviation from Frequency distribution
( classified scores/data)
e.g.2 (May 2018)
Quartile Deviation=?
CI f ( frequency)
37-39 1
34-36 3
31-33 4
28-30 3
15-27 8
22-24 5
19-21 9
16-18 7
13-15 5
10-12 9

14. Exercise:FindtheQuartiledeviationforthe following
frequencydistributions

15. Measures of Variability: SD
Standard Deviation:
The word Standard deviation was Coined by Karl Pearson.
It is denoted by σ (sigma) or SD.
SD is the most reliable and stable measures of variability.

16. Computation of SD from ungrouped scores
Eg.1 Series(A) 4,8,12,16,20
X (scores) d= X-M d2
4 (4-12) = -8 64
8 (8-12) = -4 16
12 0 0
16 +4 16
20 +8 64
∑X = 60 ∑d2= 160
∑X 60
M= ------ = ------ = 12
N 5
∑d2 160
SD = ------- = --------- = 32 = 5.657
√ N √ 60 √
SD= 5.657

17. Computation of SD from ungrouped scores
Eg.2
X f fX d= X-M fd fd2
25 2 50 (25-15)=10 20 200
20 3 60 5 15 75
15 10 150 0 0 0
10 3 30 -5 -15 75
5 2 10 -10 -20 200
N=20 ∑fX = 300 ∑fd2= 550
∑fX 300
M= ------ = ------ = 15
N 20
∑fd2 550
SD = ------- = --------- = 27.5 = 5.244
√ N √ 20 √
SD= 5.244

18. Computationof SD from grouped scores ( short method)
Eg.2
CI f d fd fd2
35-39 5 +3 +15 45
30-34 6 +2 +12 +35 24
25-29 8 +1 +8 8
20-24 10 0 0 0
15-19 5 -1 -5 5
10-14 4 -2 -8 -19 16
5-9 2 -3 -6 18
N=40 ∑fd= 16 ∑fd2= 116

20. Computationof SD from grouped scores ( short method)
Eg.2
May
2019
CI f d fd fd2
60-69 5
50-59 7
40-49 8
30-39 9
20-29 5
10-19 4
0-09 2
N= ∑fd= ∑fd2=

21. Exercise:Findthe Standarddeviationforthe following
frequencydistributions