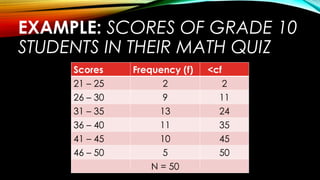
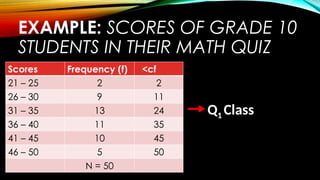
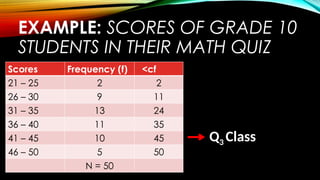
The document outlines measures of variation and dispersion in statistics, focusing on calculating the range, quartile deviation, and their interpretations for both ungrouped and grouped data. It provides detailed examples and steps for analyzing the scores of students in a quiz, including finding quartiles and interpreting interquartile ranges. Additionally, it includes an assignment task related to calculating and interpreting these measures based on a frequency distribution of student scores.

1. MEASURES OF
VARIATION
BY: MARJORIE D. BALBUENA

2. LEARNING OBJECTIVES:
•Calculate measures of dispersion
•Provide a sound interpretation of
these measures

3. TWO TYPES OF VARIABILITY OR DISPERSION

4. ABSOLUTE MEASURES OF
DISPERSION

6. Ungrouped Data:
Subtract the lowest score from the
highest score.
Range = H – L

7. Ungrouped Data:
Find the range of the distribution if the
highest score is 100 and the lowest
score is 21.

8. Ungrouped Data:
Find the range of the distribution if the
highest score is 100 and the lowest score
is 21.
Solution:
Range = H – L
Range = 100 – 21
Range = 79

9. WHAT IS THE RANGE?

10. WHAT IS THE
RANGE?
Range = H - L
Range = 50 – 10
Range = 40

11. Grouped Data:
To find the range for a frequency
distribution, just get the differences
between the upper limit of the highest
score and the lower limit of the lowest
class interval.

12. Example: Find the range for the frequency
distribution
Class Interval Frequency
100 - 104 4
105 – 109 6
110 – 114 10
115 – 119 13
120 – 124 8
125 – 129 6
130 - 134 3
N = 50

13. Range = Highest Class Upper Limit –
Lowest Class Lower Limit
Range = 134.5 – 99.5
Range = 35

14. QUARTILE DEVIATION

20. QUARTILES

23. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR UNGROUPED DATA

24. EXAMPLE:

25. ARRANGED
IN ORDER:

26. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR UNGROUPED DATA

27. ASSIGN
SERIAL
NUMBERS:

28. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR UNGROUPED DATA

29. Q1

30. Interpretation: 25% of the students have a score less than or
equal to 21.5.

31. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR UNGROUPED DATA

32. Q1
Q3

33. Interpretation: 75% of the students have a score less than or
equal to 30.5.

34. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR UNGROUPED DATA

35. ANSWER:

36. Interpretation: If the scores of
8 students in their
management statistics quiz
have a quartile deviation of
4.5, it means that the middle
50% of the scores (from the
25th percentile to the 75th
percentile) deviate from the
median by approximately 4.5
points.

37. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR GROUPED DATA
Step 1: Find the class interval in
which the first quartile (Q1) falls.

38. EXAMPLE: SCORES OF GRADE 10
STUDENTS IN THEIR MATH QUIZ
Scores Frequency (f) <cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50

39. EXAMPLE: SCORES OF GRADE 10
STUDENTS IN THEIR MATH QUIZ
Scores Frequency (f) <cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
=

40. EXAMPLE: SCORES OF GRADE 10
STUDENTS IN THEIR MATH QUIZ
Scores Frequency (f) <cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q1 Class

41. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR GROUPED DATA
Step 2: Find Q1
Formula:
Q1 = L +
L
i
𝐜𝐟 𝐛
f
n

42. EXAMPLE: SCORES OF GRADE 10
STUDENTS IN THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q1 Class
Q1 = L +
L = 31 – 0.5 = 30.5
=
= 11
f = 13
i = 5

43. EXAMPLE: SCORES OF GRADE 10 STUDENTS IN
THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q1
Class
Q1 = L +
L = 30.5 ; = ; i = 5
Q1 = 30.5 +
Q1 = 30.5 +
Q1 = 30.5 +
Q1 = 30.5 + 0.58
Q1 = 31.08

44. EXAMPLE: SCORES OF GRADE 10 STUDENTS IN
THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q1
Class
Q1 = L +
Q1 = 30.5 +
Q1 = 30.5 +
Q1 = 30.5 +
Q1 = 30.5 + 0.58
Q1 = 31.08
Interpretation: 25% of the students have a score less than
or equal to 31.08.

45. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR GROUPED DATA
Step 3: Find the class interval in
which the third quartile (Q3) falls.

46. EXAMPLE: SCORES OF GRADE 10
STUDENTS IN THEIR MATH QUIZ
Scores Frequency (f) <cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
=

47. EXAMPLE: SCORES OF GRADE 10
STUDENTS IN THEIR MATH QUIZ
Scores Frequency (f) <cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q3 Class

48. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR GROUPED DATA
Step 4: Find Q3
Formula:
Q3 = L +
L
i
𝐜𝐟 𝐛
f
n

49. EXAMPLE: SCORES OF GRADE 10
STUDENTS IN THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q3 Class
Q3 = L +
L = 41 – 0.5 = 40.5
=
= 35
f = 10
i = 5

50. EXAMPLE: SCORES OF GRADE 10 STUDENTS IN
THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q3
Class
Q3 = L +
L = 40.5 ; = ; i = 5
Q3 = 40.5 +
Q3 = 40.5 +
Q3 = 40.5 +
Q3 = 40.5 + 1.25
Q3 = 41.75

51. EXAMPLE: SCORES OF GRADE 10 STUDENTS IN
THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q3
Class
Q3 = L +
Q3 = 40.5 +
Q3 = 40.5 +
Q3 = 40.5 +
Q3 = 40.5 + 1.25
Q3 = 41.75
Interpretation: 75% of the students have a score less than
or equal to 41.75.

52. STEPS IN CALCULATING THE QUARTILE
DEVIATION FOR GROUPED DATA
Step 5: Calculate for interquartile range and quartile
deviation.
Formulas:
IQR = Q3 – Q1
QD =

53. EXAMPLE: SCORES OF GRADE 10 STUDENTS IN
THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q1 = 31.08 ; Q3 = 41.75
IQR = Q3 – Q1
IQR = 41.75– 31.08
IQR = 10.67

54. EXAMPLE: SCORES OF GRADE 10 STUDENTS IN
THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
IQR = 10.67
Interpretation: When the IQR is given as
10.67 for the scores of grade 10 students
in their math quiz, it means that the
middle 50% of the scores (from the 25th
percentile to the 75th percentile) fall
within a range of 10.67. This range
provides insights into the spread of the
scores among the students.

55. EXAMPLE: SCORES OF GRADE 10 STUDENTS IN
THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Q1 = 31.08 ; Q3 = 41.75
QD =
QD =
QD = 5.34
QD =

56. EXAMPLE: SCORES OF GRADE 10 STUDENTS IN
THEIR MATH QUIZ
Scores Frequency
(f)
<cf
21 – 25 2 2
26 – 30 9 11
31 – 35 13 24
36 – 40 11 35
41 – 45 10 45
46 – 50 5 50
N = 50
Interpretation: When the quartile
deviation is given as 5.34 for the scores of
grade 10 students in their math quiz, it
means that the middle 50% of the scores
(from the 25th percentile to the 75th
percentile) deviate from the median by
approximately 5.34 points.
QD = 5.34

57. ASSIGNMENT:
• Consider the frequency distribution of scores of the
students in Mathematics. Find a) Q1 ; b) Q3 ; c) IQR with
interpretation ; d) QD with interpretation [20 points]
Class Interval Frequency (f) <cf
88 – 96 9 65
80 – 87 10 56
72 – 79 15 46
64 - 71 13 31
56 - 63 9 18
48 - 55 9 9
N = 65