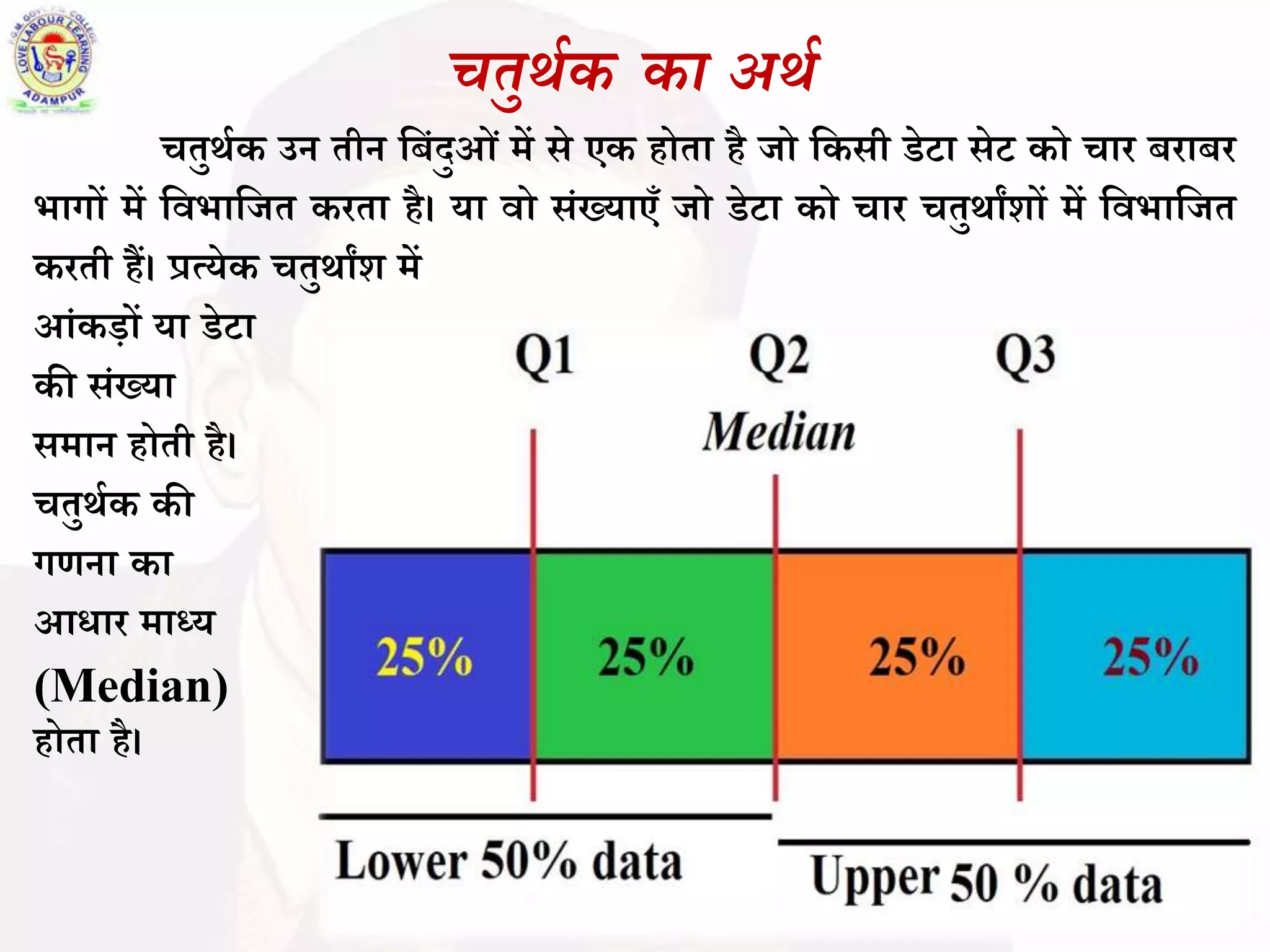
चतुर्थक उन तीन बिंदुओं में से एक होता है जो किसी डेटा सेट को चार बराबर भागों में विभाजित करता है। या वो संख्याएँ जो डेटा को चार चतुर्थांशों में विभाजित करती हैं। प्रत्येक चतुर्थांश में आंकड़ों या डेटा की संख्या
समान होती है। चतुर्थक की गणना का आधार माध्य (Median) होता है।