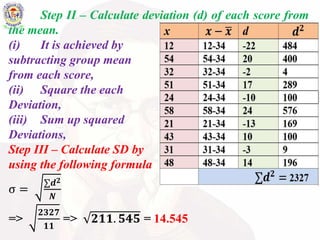
The document discusses standard deviation (SD) as a measure of variability in a data set, detailing its definition, significance in statistics, and characteristics such as its relationship with mean values. It provides methods for computing SD for ungrouped and grouped data along with examples. Additionally, it addresses how SD indicates data dispersion and its application in statistical techniques.

1. Standard
Deviation
Dr Rajesh Verma
Asst. Prof (Psychology)
Govt. College Adampur,
Hisar, HaryanaPC Mahalanobis, Indian Legend

2. Meaning-Cum-Definition
It’s a quantity that indicates by how much the
members of a group differ from the mean value for the
group.
Standard deviation is and index of degree of
dispersion and an estimate of the variability in the
population from which the sample is drawn (Guilford
& Fruchter,
1976).

3. Introduction
SD is also known as Coefficient of Variation (CV). It’s
a kind of special average of all the deviation from the group
mean. Special average means that SD is beyond the simple
arithmetic mean. Along with the total range, semi-
interquartile range, average deviation it is the most
commonly used single number to indicate
variability among a data set. Variability is
the scatter or spread of the separate scores
around their central tendency (Garret, 2014).
SD is the most stable index of variability
which is computed using squared deviations
that are taken from mean only i.e. neither
median nor mode.

4. Characteristics
(i) High value of SD means that most of the scores are
away from group mean and vice versa.
(ii) It is the index of spread of scores about the mean that
involves every observation.
(iii) Greater SD than mean indicates
that the distribution have majority of
low values.
(iv) Lower SD than mean indicates
that the distribution have majority
of high values.
(v) It can also indicate that whether
the distribution has dispersion of
extreme values or has
central tendency.

5. (vi) It is expressed in the same units as the data.
(vii) It is possible to calculate the combined standard
deviation of two or more groups.
(viii) The SD is considered most appropriate statistical tool
for comparing the variability of two or more groups.
(ix) It is used as unit of measurement in normal
probability distribution.
(x) SD forms the base for
several statistical techniques
such skewness, kurtosis,
ANOVA etc.

6. How much SD is Good or Bad
No amount of SD is good or bad because it’s just an
indicator of spread of scores. If someone is interested to see
the closeness of scores around the mean than SD ≤ 1 is good,
on the other hand if someone is interested in larger spread
than SD ≥ 1 is good. Across books and manuals it has been
accepted that SD ≥ 1 is the
indicator of high variation
among the scores and SD ≤ 1
indicates low variation. It’s a
kind of rule of thumb.
In fact it depend upon
the data set and objectives of
the researcher.

7. Computation of SD
For Ungrouped Data
Let us take an hypothetical data.
Ex – 12, 54, 32, 51, 24, 58, 21, 43, 31, 48
Step I – Calculate the mean.
Mean ( 𝒙) =
∑𝒙
𝑵
Where, x = Score
N = total no. of score
Therefore, 12+54+32+51+24
+58+21+43+31+48 = 374
𝒙 =
𝟑𝟕𝟒
𝟏𝟏
= 34

8. Step II – Calculate deviation (d) of each score from
the mean.
(i) It is achieved by
subtracting group mean
from each score,
(ii) Square the each
Deviation,
(iii) Sum up squared
Deviations,
Step III – Calculate SD by
using the following formula
σ =
∑𝒅 𝟐
𝑵
=>
𝟐𝟑𝟐𝟕
𝟏𝟏
=> 𝟐𝟏𝟏. 𝟓𝟒𝟓 = 14.545

9. SD of Grouped Data
Let us take Hypothetical Data
as shown in adjacent table
Step I - Calculate the mean
For calculation of mean we must
follow the following few steps

10. Steps of calculating mean
(i) Find the midpoints of CI (x)
(ii) Multiply midpoints (x) with their respective
frequency (f)
(iii) Add fx
(iv) Divide it by the sum of
frequencies i.e. 50
mean =
∑𝒇 𝒙
𝑵
=
𝟏𝟔𝟓𝟎
𝟓𝟎
= 33

11. Step II-Subtract mean from the mid points i.e. 𝒙 − 𝒙
Step III-Square these values which are denoted by (x`)
Step IV-Multiply x` with their respective frequencies (fx`)
Step V-Add fx`
Finally substitute the values in the formula
σ =
∑𝒇𝒙`
𝑵
=
𝟓𝟓𝟏𝟐
𝟓𝟎
= 𝟏𝟏𝟎. 𝟐𝟒
(𝒔 𝟐
= 110.24)
= 10.499

12. References:
1. https://dictionary.apa.org/quartile-deviation.
2. Guilford, J. P. and Fruchter, B. (1978). Fundamental Statistics in
Psychology and Education, 6th ed. Tokyo: McGraw-Hill.
3. https://todayinsci.com/M/Mahalanobis_Prasanta/
MahalanobisPrasanta-Quotations.htm.
4. Garrett, H. E. (2014). Statistics in Psychology and Education. New
Delhi: Pragon International.
5. Levin, J. & Fox, J. A. (2006). Elementary Statistics.
New Delhi: Pearson.

13. vermasujit@yahoo.com
Next
Discussion
Concept of
Normality