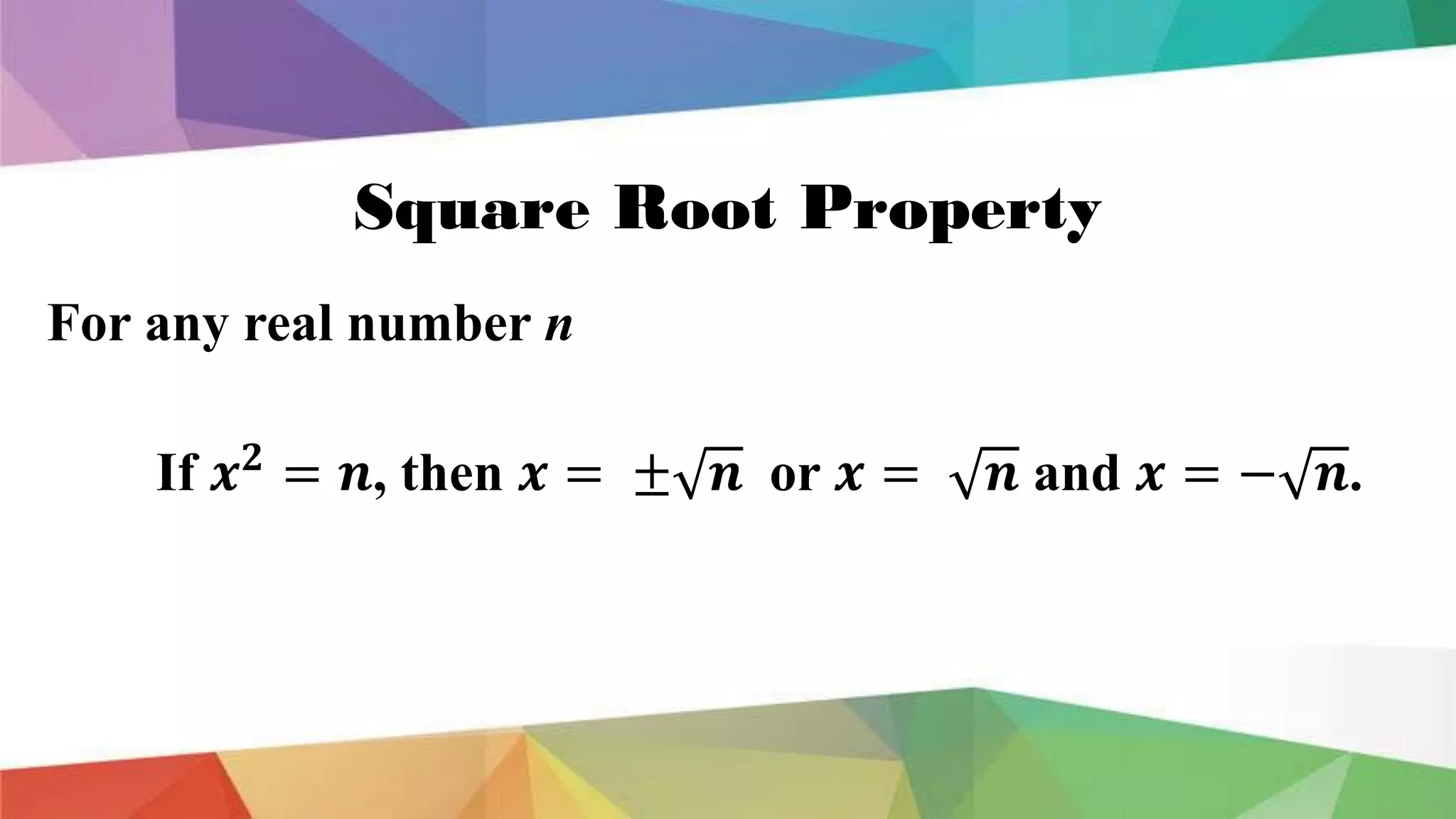The document provides methods for solving quadratic equations including extracting square roots, factoring, completing the square, and using the quadratic formula. It includes detailed steps, examples, and checks for each method to verify solutions. Key concepts such as the solution set and the zero product property are also explained.

1. Solving Quadratic Equations
• Extracting Square Roots
• Factoring
• Completing the Square
• Quadratic Formula

2. •Any value that satisfies an equation is called a
solution.
•The set of solution that satisfy an equation is
called solution set.
•The solution is also called root.
In solving quadratic equations, it means
finding its solution(s) or root(s) that will satisfy
the given equation.

3. Solving Quadratic Equation
by
Extracting the Square Roots

4. Let’s Practice
• 𝒙𝟐 = 𝒙
• 𝟐𝟓 = 𝟓
• 𝟗𝟖 = (𝟒𝟗)(𝟐) = 𝟕 𝟐
• (𝒙 − 𝟑)𝟐= 𝒙 − 𝟑
•
𝟒
𝟐𝟓
=
𝟐
𝟓

5. Square Root Property
For any real number n
If 𝒙𝟐
= 𝒏, then 𝒙 = ± 𝒏 or 𝒙 = 𝒏 and 𝒙 = − 𝒏.

6. Reminder:
Before using the square root property,
make sure that the equation is in the form
x2 = n.

7. Steps in Solving Quadratic
Equation by Extracting the
Square Root
1. Write the equation in the form
x2 = n.
2. Use the square root property.
3. Solve for x.
Example 1:
𝑥2
= 100
𝑥2 = 100
𝑥 = ±10
𝒙 = 𝟏𝟎 𝒐𝒓 𝒙 = −𝟏𝟎
Checking:
𝑥 = 10 𝑥 = −10
𝑥2
= 100 𝑥2
= 100
(10)2
= 100 (−10)2
= 100
100 = 100 100 = 100

8. Example 2:
𝑥2
− 121 = 0
𝑥2
− 121 + 121 = 0 + 121
𝑥2
= 121
𝑥2 = 121
𝑥 = ±11
𝒙 = 𝟏𝟏 𝒐𝒓 𝒙 = −𝟏𝟏
Checking:
𝑥 = 11 𝑥 = −11
𝑥2
− 121 = 0 𝑥2
− 121 = 0
(11)2
−121 = 0 (−11)2
−121 = 0
121 − 121 = 0 121 − 121 = 0
0 = 0 0 = 0
Steps in Solving Quadratic
Equation by Extracting the
Square Root
1. Write the equation in the form
x2 = n.
2. Use the square root property.
3. Solve for x.

9. Example 3:
(𝑥 − 3)2
= 9
(𝑥 − 3)2 = 9
𝑥 − 3 = ±3
𝑥 − 3 + 3 = ±3 + 3
𝑥 = ±3 + 3
𝒙 = 𝟑 + 𝟑 = 𝟔 𝒐𝒓 𝒙 = −𝟑 + 𝟑 = 𝟎
Checking:
𝑥 = 6 𝑥 = 0
(𝑥 − 3)2
= 9 (𝑥 − 3)2
= 9
(6 − 3)2
= 9 (0 − 3)2
= 9
(3)2
= 9 (−3)2
= 9
9 = 9 9 = 9
Steps in Solving Quadratic
Equation by Extracting the
Square Root
1. Write the equation in the form
x2 = n.
2. Use the square root property.
3. Solve for x.

10. Example 4:
𝑥2
+ 4 = 4
𝑥2
+ 4 − 4 = 4 − 4
𝑥2
= 0
𝑥2 = 0
𝒙 = 𝟎
Checking:
𝑥 = 0
𝑥2
+ 4 = 4
(0)2
+4 = 4
0 + 4 = 4
4 = 4
Steps in Solving Quadratic
Equation by Extracting the
Square Root
1. Write the equation in the form
x2 = n.
2. Use the square root property.
3. Solve for x.

11. Example 5:
4𝑥2
− 1 = 0
4𝑥2
− 1 + 1 = 0 + 1
4𝑥2
= 1
4𝑥2
4
=
1
4
𝑥2
=
1
4
𝑥2 =
1
4
𝑥 = ±
1
2
𝒙 =
𝟏
𝟐
𝒐𝒓 𝒙 = −
𝟏
𝟐
Checking:
𝑥 =
1
2
𝑥 = −
1
2
4𝑥2
− 1 = 0 4𝑥2
− 1 = 0
4
1
2
2
− 1 = 0 4 −
1
2
2
− 1 = 0
4
1
4
− 1 = 0 4
1
4
− 1 = 0
4
4
− 1 = 0
4
4
− 1 = 0
1 − 1 = 0 1 − 1 = 0
0 = 0 0 = 0
Steps in Solving
Quadratic Equation
by Extracting the
Square Root
1. Write the equation
in the form x2 = n.
2. Use the square root
property.
3. Solve for x.

12. Example 6:
3𝑥2
= −9
3𝑥2
3
=
−9
3
𝑥2
= −3
𝑥2 = −3
𝒙 = ± −𝟑
Take note that
when n < 0, then the
quadratic equation
has no real solution.

13. Solving Quadratic Equation
by
Factoring

14. Steps in Solving Quadratic Equation
by Factoring.
1. Write the quadratic equation in standard form.
2. Find the factors of the quadratic expression.
3. Apply the Zero Product Property.
4. Solve each resulting equation.
5. Check the values of the variable obtained by substituting each in the
original equation.

15. Zero Product Property
The product AB = 0, if and only if
A = 0 or B = 0.

16. Example 1:
𝑥2
− 6𝑥 + 8 = 0
𝑥 − 4 𝑥 − 2 = 0
𝑥 − 4 = 0
𝑥 − 4 + 4 = 0 + 4
𝒙 = 𝟒
𝑥 − 2 = 0
𝑥 − 2 + 2 = 0 + 2
𝒙 = 𝟐
x = 4 or x = 2
Checking:
x = 4
𝑥2
−6𝑥 + 8 = 0
(4)2
−6(4) + 8 = 0
16 − 24 + 8 = 0
0 = 0
x = 2
𝑥2
−6𝑥 + 8 = 0
(2)2
−6(2) + 8 = 0
4 − 12 + 8 = 0
0 = 0

17. Example 2:
𝑥2 + 6 = −5𝑥
𝑥2 + 6 + 5𝑥 = −5𝑥 + 5𝑥
𝑥2
+ 5𝑥 + 6 = 0
𝑥 + 2 𝑥 + 3 = 0
𝑥 + 2 = 0
𝑥 + 2 − 2 = 0 − 2
𝒙 = −𝟐
𝑥 + 3 = 0
𝑥 + 3 − 3 = 0 − 3
𝒙 = −𝟑
𝒙 = −𝟐 𝒐𝒓 𝒙 = −𝟑
Checking:
x = -2
𝑥2
+6 = −5𝑥
(−2)2
+6 = −5(−2)
4 + 6 = 10
10 = 10
x = -3
𝑥2
+ 6 = −5𝑥
(−3)2
+ 6 = −5(−3)
9 + 6 = 15
15 = 15

18. Example 3:
2𝑥2
+ 15𝑥 = −27
2𝑥2
+ 15𝑥 + 27 = −27 + 27
2𝑥2
+ 15𝑥 + 27 = 0
2𝑥 + 9 𝑥 + 3 = 0
2𝑥 + 9 = 0
2𝑥 + 9 − 9 = 0 − 9
2𝑥 = −9
2𝑥
2
= −
9
2
𝒙 = −
𝟗
𝟐
𝑥 + 3 = 0
𝑥 + 3 − 3 = 0 − 3
𝒙 = −𝟑
𝒙 = −
𝟗
𝟐
𝒐𝒓 𝒙 = −𝟑
Checking:
x = −
9
2
2𝑥2
+15𝑥 = −27
2(−
9
2
)2
+ 15 −
9
2
= −27
2
81
4
−
135
2
= −27
81
2
−
135
2
= −27
−
54
2
= −27
−27 = −27
x = -3
2 𝑥2
+15𝑥 = −27
2(−3)2
+ 15(−3) = −27
2 9 − 45 = −27
18 − 45 = −27
−27 = −27

19. Example 4:
𝑥2
− 6𝑥 = 0
𝑥 𝑥 − 6 = 0
𝒙 = 𝟎
𝑥 − 6 = 0
𝑥 − 6 + 6 = 0 + 6
𝒙 = 𝟔
𝒙 = 𝟎 𝒐𝒓 𝒙 = 𝟔
Checking:
x = 0
𝑥2
− 6𝑥 = 0
(0)2
−6 0 = 0
0 − 0 = 0
0 = 0
x = 6
𝑥2
− 6𝑥 = 0
(6)2
−6(6) = 0
36 − 36 = 0
0 = 0

20. Example 5:
𝑥2
− 36 = 0
𝑥 + 6 𝑥 − 6 = 0
𝑥 + 6 = 0
𝑥 + 6 − 6 = 0 − 6
𝒙 = −𝟔
𝑥 − 6 = 0
𝑥 − 6 + 6 = 0 + 6
𝒙 = 𝟔
𝒙 = −𝟔 𝒐𝒓 𝒙 = 𝟔
Checking:
x = -6
𝑥2
−36 = 0
(−6)2
−36 = 0
36 − 36 = 0
0 = 0
x = 6
𝑥2
− 36 = 0
(6)2
− 36 = 0
36 − 36 = 0
0 = 0

21. Solving Quadratic Equation
by
Completing the Square

22. Steps in Solving Quadratic Equation by
Completing the Square
1. If the value of a = 1, proceed to step 2. Otherwise, divide both
sides of the equation by a.
2. Group all the terms containing a variable on one side of the
equation and the constant term on the other side. That is
ax2 + bx = c.
3. Complete the square of the resulting binomial by adding the
square of the half of b on both sides of the equation.
𝑏
2
2
4. Rewrite the perfect square trinomial as the square of binomial.
𝑥 +
𝑏
2
2
.
5. Use extracting square the square root to solve for x.

23. Example 1:
𝑥2 + 2𝑥 − 8 = 0
Since a = 1, let’s proceed with step 2.
Group all the terms containing a variable on one side of the equation
and the constant term on the other side. That is ax2 + bx = c.
𝑥2 + 2𝑥 − 8 = 0
𝑥2 + 2𝑥 − 8 + 8 = 0 + 8
𝑥2 + 2𝑥 = 8
Complete the square of the resulting binomial by adding the
square of the half of b on both sides of the equation.
𝑏
2
2
𝑏
2
2
=
2
2
2
= 12 = 𝟏
𝑥2 + 2𝑥 + 1 = 8 + 1
𝑥2 + 2𝑥 + 1 = 9
Rewrite the perfect square trinomial as the square of binomial.
𝑥 +
𝑏
2
2
.
(𝑥 + 1)2 = 9
Use extracting square the square root to solve for x.
𝑥 + 1 2 = 9
𝑥 + 1 = ±3
x + 1 = 3 x + 1 = –3
x +1 – 1 = 3 – 1 x + 1 – 1 = –3 – 1
x = 2 x = – 4
Checking:
x = 2 x = – 4
𝑥2 + 2𝑥 − 8 = 0 𝑥2 + 2𝑥 − 8 = 0
(2)2 + 2(2) – 8 = 0 (-4) + 2(-4) – 8 = 0
4 + 4 – 8 = 0 16 – 8 – 8 = 0
8 – 8 = 0 8 – 8 = 0
0 = 0 0 = 0

24. Example 2:
2𝑥2 − 12𝑥 = 54
Since a ≠ 1, we divide both sides of the equation by a. a = 2
2𝑥2
2
−
12𝑥
2
=
54
2
→ 𝑥2
− 6𝑥 = 27
Group all the terms containing a variable on one side of the equation
and the constant term on the other side. That is ax2 + bx = c.
𝑥2 − 6𝑥 = 27
Complete the square of the resulting binomial by adding the
square of the half of b on both sides of the equation.
𝑏
2
2
𝑏
2
2
=
6
2
2
= 32 = 𝟗
𝑥2 − 6𝑥 + 9 = 27 + 9
𝑥2 − 6𝑥 + 9 = 36
Rewrite the perfect square trinomial as the square of binomial.
𝑥 +
𝑏
2
2
.
(𝑥 − 3)2 = 36
Use extracting square the square root to solve for x.
𝑥 − 3 2 = 36
𝑥 − 3 = ±6
x – 3 = 6 x – 3 = –6
x – 3 + 3 = 6 + 3 x – 3 = –6 + 3
x = 9 x = – 3
Checking:
x = 9 x = – 3
2𝑥2 − 12𝑥 = 54 2𝑥2 − 12𝑥 = 54
2(9)2 – 12(9) = 54 2(-3)2 – 12(-3) = 54
2(81) – 108 = 54 2(9) +36 = 54
162 – 108 = 54 18 + 36 = 54
54 = 54 54 = 54

25. Example 3:
4𝑥2 + 16𝑥 − 9 = 0
Since a ≠ 1, we divide both sides of the equation by a. a = 4
4𝑥2
4
+
16𝑥
4
−
9
4
=
0
4
→ 𝑥2 + 4𝑥 −
9
4
= 0
Group all the terms containing a variable on one side of the equation
and the constant term on the other side. That is ax2 + bx = c.
𝑥2
+ 4𝑥 −
9
4
= 0 → 𝑥2
+ 4𝑥 −
9
4
+
9
4
= 0 +
9
4
𝒙𝟐 + 𝟒𝒙 =
𝟗
𝟒
Complete the square of the resulting binomial by adding the
square of the half of b on both sides of the equation.
𝑏
2
2
𝑏
2
2
=
4
2
2
= 22 = 4
𝑥2 + 4𝑥 + 4 =
9
4
+ 4
𝑥2
+ 4𝑥 + 4 =
25
4
Rewrite the perfect square trinomial as the square of binomial.
𝑥 +
𝑏
2
2
.
(𝑥 + 2)2 =
25
4
Use extracting square the square root to solve for x.
𝑥 + 2 2 =
25
4
𝑥 + 2 = ±
5
2
𝑥 + 2 =
5
2
𝑥 + 2 = −
5
2
𝑥 + 2 − 2 =
5
2
− 2 𝑥 + 2 − 2 = −
5
2
− 2
𝒙 =
𝟏
𝟐
𝒙 = −
𝟗
𝟐
Checking:
x =
1
2
x = –
9
2
4𝑥2 + 16𝑥 − 9 = 0 4𝑥2 + 16𝑥 − 9 = 0
4
1
2
2
+ 16
1
2
− 9 = 0 4 −
9
2
2
+ 16 −
9
2
− 9 = 0
4
1
4
+ 8 − 9 = 0 4
81
4
− 72 − 9 = 0
1 + 8 – 9 = 0 81 – 72 – 9 = 0
0 = 0 0 = 0

26. Solving Quadratic Equation
by
Quadratic Formula

27. QUADRATIC FORMULA
𝒙 =
−𝒃 ± 𝒃𝟐 − 𝟒𝒂𝒄
𝟐𝒂

28. Example 1:
𝑥2
− 𝑥 − 6 = 0
𝑎 = 1, 𝑏 = −1, 𝑐 = −6
Solution:
𝑥 =
−𝑏± 𝑏2−4𝑎𝑐
2𝑎
𝑥 =
− −1 ± (−1)2−4 1 −6
2(1)
𝑥 =
1± 1+24
2
𝑥 =
1± 25
2
𝑥 =
1±5
2
𝑥 =
1+5
2
=
6
2
= 𝟑
𝑥 =
1−5
2
=
−4
2
= −𝟐
Checking:
x = 3 x = – 2
𝑥2
− 𝑥 − 6 = 0 𝑥2
− 𝑥 − 6 = 0
(3)2 – (3) – 6 = 0 (-2)2 – (-2) – 6 = 0
9 – 3 – 6 = 0 4 + 2 – 6 = 0
6 – 6 = 0 6 – 6 = 0
0 = 0 0 = 0
Note:
Before using the quadratic formula in solving
quadratic equations, make sure that the quadratic
equation is in standard form in order to properly
identify the values of a, b, and c.

29. Example 2:
5𝑥2
+ 6𝑥 = −1
5𝑥2
+ 6𝑥 + 1 = −1 + 1
5𝑥2
+ 6𝑥 + 1 = 0
𝑎 = 5, 𝑏 = 6, 𝑐 = 1
Solution:
𝑥 =
−𝑏± 𝑏2−4𝑎𝑐
2𝑎
𝑥 =
− 6 ± (6)2−4 5 1
2(5)
𝑥 =
−6± 36−20
10
𝑥 =
−6± 16
10
𝑥 =
−6±4
10
𝑥 =
−6+4
10
=
−2
10
= −
𝟏
𝟓
𝑥 =
−6−4
10
=
−10
10
= −𝟏
Checking:
x = −
1
5
x = – 1
5𝑥2
+ 6𝑥 = −1 5𝑥2
+ 6𝑥 = −1
5 −
1
5
2
+ 6 −
1
5
= −1 5(−1)2+6(−1) = −1
1
5
−
6
5
= −1 5 − 6 = −1
−
5
5
= −1 −1 = −1
− 1 = −1
Note:
Before using the quadratic formula in solving
quadratic equations, make sure that the quadratic
equation is in standard form in order to properly
identify the values of a, b, and c.