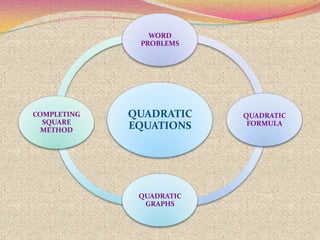
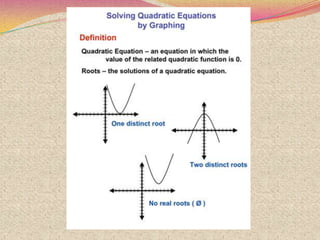
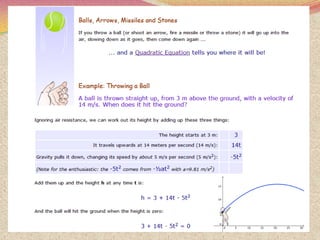
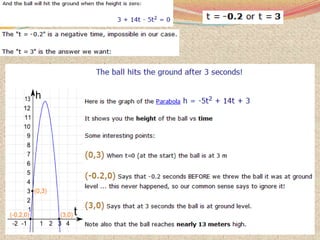
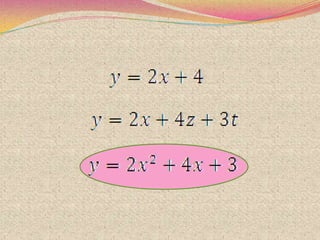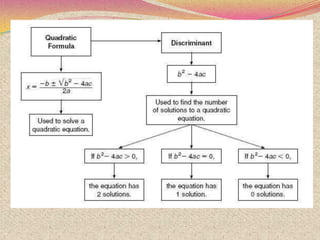
The document discusses various topics relating to quadratic equations including: 1) Methods for solving quadratic equations such as completing the square, factorization, and the quadratic formula. 2) The steps for using the completing the square method which involves rewriting the quadratic in the form of a perfect square trinomial. 3) Examples are provided to demonstrate how to use completing the square to solve quadratic equations.

1. Presenter:
HUMAIRA FARAZ

2. BASIC
ALGEBRA
• ax+b ; 2x-7
• Difference b/w
expression and
equations
SOLVE BASIC
EQUATIONS
• 2x-8=4
• 2/x + 7 = 5/x
QUADRATIC
EQUATIONS? • ax² + bx + c = 0 (a ≠ 0)
SOLVE
QUADRATIC
EQUATIONS.
• Square root property.
• Algebraic Formula
• Factorization.

3. QUADRATIC
EQUATIONS
WORD
PROBLEMS
QUADRATIC
FORMULA
QUADRATIC
GRAPHS
COMPLETING
SQUARE
METHOD

8. Factorization (Examples)
Example 1
x2
– 2x – 24 = 0
x2
– 6x + 4x – 24 = 0
(x + 4)(x – 6) = 0
x + 4 = 0 x – 6 = 0
 x = –4 x = 6
Example 2
x
2
– 8x + 11 = 0
x
2
– 8x + 11 is prime;
therefore, another
method must be used
to solve this equation.

9. COMPLETING
SQUARE
METHOD

10. (x + 4)2
x + 4
x
+
4
x2 4x
4x 16
Completing The Square
Some quadratic functions can written as a perfect squares.
x2 + 8x + 16 x2 + 10x + 25
(x + 5)2
x + 5
x 5x
25
+
5 5x
x2
We can show this
geometrically when
the coefficient of x is
positive.
When we write
expressions in this
form it is known as
completing the
square.

11. Completing The Square
Some quadratic functions can written as a perfect square.
x2 + 8x + 16
(x + 4)2
(x - 2)2
x2 - 4x + 4
Similarly when the coefficient of x is negative:
What is the relationship
between the constant term
and the coefficient of x?
The constant term is always (half the coefficient of x)2.

12. Completing The Square
x2 + 3x + 2.25
(x + 1.5)2
(x - 3.5)2
x2 - 7x + 12.25
When the coefficient of x is odd we can still write a quadratic expression as a non-
perfect square, provided that the constant term is (half the coefficient of x)2

13. = (x + 2)2
= (x - 3)2
x2 + 4x
x2 - 6x
Completing The Square
This method enables us to write equivalent expressions for quadratics of
the form ax2 + bx. We simply half the coefficient of x to complete the
square then remember to correct for the constant term.
- 4
- 9

14. = (x + 1.5)2
= (x - 3.5)2
x2 + 3x x2 - 7x
Completing The Square
This method enables us to write equivalent expressions for quadratics of
the form ax2 + bx. We simply half the coefficient of x to complete the
square then remember to correct for the constant term.
- 2.25 - 12.25

15. = (x + 5)2= (x + 2)2
= (x - 1)2
= (x - 6)2
x2 + 4x + 3 x2 + 10x + 15
x2 - 2x + 10 x2 - 12x - 1
Completing The Square
We can also write equivalent expressions for quadratics of the form
ax2 + bx + c. Again, we simply half the coefficient of x to complete the square
and remember to take extra care in correcting for the constant term.
- 1 - 10
+ 9 - 37

16. Solving Quadratic Equations
by Completing the Square
Solve the following
equation by
completing the
square:
Step 1: Move
quadratic term, and
linear term to left
side of the equation
2
8 20 0x x
2
8 20x x

17. Solving Quadratic Equations
by Completing the Square
Step 2: Find the term
that completes the square
on the left side of the
equation. Add that term to
both sides.
2
8 =20 +x x  
21
( ) 4 then square it, 4 16
2
8
2
8 2016 16x x

18. Solving Quadratic Equations
by Completing the Square
Step 3: Factor
the perfect
square trinomial
on the left side
of the equation.
Simplify the right
side of the
equation.
2
8 2016 16x x

19. Solving Quadratic Equations by
Completing the Square
Step 4:
Take the
square root
of each
side
2
( 4) 36x
( 4) 6x

20. Solving Quadratic Equations by
Completing the Square
Step 5: Set
up the two
possibilities
and solve
4 6
4 6 and 4 6
10 and 2x=
x
x x
x

21. Completing the Square-Example #2
Solve the following
equation by completing
the square:
Step 1: Move quadratic
term, and linear term to
left side of the equation,
the constant to the right
side of the equation.
2
2 7 12 0x x
2
2 7 12x x

22. Solving Quadratic Equations by
Completing the Square
Step 2: Find the term
that completes the square
on the left side of the
equation. Add that term
to both sides.
The quadratic coefficient
must be equal to 1 before
you complete the square, so
you must divide all terms
by the quadratic
coefficient first.
2
2
2
2 7
2
2 2 2
7 12
7
2
=-12 +
6
x x
x x
xx  
 
 
2
1 7 7 49
( ) then square it,
2 62 4 4 1
7
2 49 49
16 1
7
6
2 6
x x

23. Solving Quadratic Equations
by Completing the Square
Step 3: Factor
the perfect
square trinomial
on the left side of
the equation.
Simplify the right
side of the
equation.
2
2
2
7
6
2
7 96 49
4 16 16
7 47
4
49 49
16 1
16
6
x x
x
x

24. Solving Quadratic Equations by
Completing the Square
Step 4:
Take the
square
root of
each side
27 47
( )
4 16
x
7 47
( )
4 4
7 47
4 4
7 47
4
x
i
x
i
x

25. QUADRATIC
FORMULA

26. 2
4
2
b b ac
x
a
THE QUADRATIC FORMULA
1. When you solve using completing the square
on the general formula
you get:
2. This is the quadratic formula!
3. Just identify a, b, and c then substitute into
the formula.
2
0ax bx c

27. 2
2 7 11 0x x
2
2
4
2
7 7 4(2)( 11)
2(
2, 7, 11
7 137
2 Reals - Irrational
4
2)
a b
b ac
a
c
b
Solve using the Quadratic Formula
X = 1.176 and -4.676

30. SCIENTIFIC CALCULATOR