Quantitative Structure Activity Relationships (QSAR) relates the biological activity of compounds to their physicochemical properties using mathematical models. QSAR equations express how properties like hydrophobicity, electronic effects, and steric hindrance of molecules and substituents influence biological response. Hydrophobicity is often quantified by log P values, while electronic and steric effects use constants like Hammett's s, Taft's Es, and molar refractivity. Successful QSAR equations incorporate multiple physicochemical terms to predict activity for new structures within the same class.

1. Quantitative Structure Activity
Relationships (QSAR)

2. Introduction
•Aims
•To relate the biological activity of a series of compounds to their
physicochemical parameters in a quantitative fashion using a mathematical
formula
•Requirements
•Quantitative measurements for biological and physicochemical properties
•Physicochemical Properties
•Hydrophobicity of the molecule
•Hydrophobicity of substituents
•Electronic properties of substituents
•Steric properties of substituents
Most common
properties studied

3. Mathematical Model
•Biological activity can be expressed quantitatively as the concentration of a
substance required to give a certain biological response.
•Additionally, when physicochemical properties are expressed by numbers, one
can form a mathematical relationship, i.e. QSAR, between the two.
•The mathematical model can then be used to predict the biological response
of other chemical structure.
•QSAR has a form of mathematical
•Biological activity is normally expressed as 1/C, where C = [drug] required to
achieve a defined level of biological activity
Activity = ƒ (Physicochemical properties) + Error

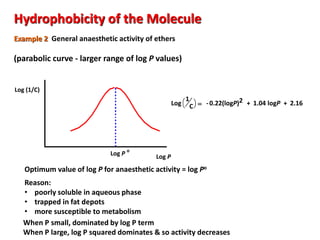
4. Hydrophobicity of the Molecule
Partition Coefficient P = [Drug in octanol]
[Drug in water]
High P High hydrophobicity

5. •Activity of drugs is often related to P
e.g. binding of drugs to serum albumin
(straight line - small range of log P, i.e. 1-4)
•Binding increases as log P increases
•Binding is greater for hydrophobic drugs
Log 1
C



= 0.75 logP + 2.30
Hydrophobicity of the Molecule
Log (1/C)
Log P
. .
.
.
. .
. .
.
0.78 3.82

6. Example 2 General anaesthetic activity of ethers
(parabolic curve - larger range of log P values)
Optimum value of log P for anaesthetic activity = log Po
Log
1
C



= -0.22(logP)2 + 1.04 logP + 2.16
Hydrophobicity of the Molecule
Log P o
Log P
Log (1/C)
Reason:
• poorly soluble in aqueous phase
• trapped in fat depots
• more susceptible to metabolism
When P small, dominated by log P term
When P large, log P squared dominates & so activity decreases

7. QSAR equations are only applicable to compounds in the same structural class
(e.g. ethers or benzodiazepins)
•Structures with log P ca. 2.3 enter the CNS easily
(e.g. potent barbiturates have a log P of approximately 2.0)
•Can alter log P value of drugs away from 2.0 to avoid CNS side effects
*RELATIVELY FEW DRUGS EXIST WHOSE ACTIVITY IS RELATED TO LOG P ALONE!!!
those that do are the general anesthetics-partition into cell membranes &
thereby affect membrane structure & nerve function
Hydrophobicity of the Molecule
Notes:

8. Hydrophobicity of Substituents
- the substituent hydrophobicity constant (p)
Notes:
•A measure of a substituent’s hydrophobicity relative to hydrogen
•Tabulated values exist for aliphatic and aromatic substituents
•Measure P experimentally for a standard compound with and without a substituent (X).
Use this equation: p X = log PX - log PH
Example:
•Positive values imply substituents are more hydrophobic than H
•Negative values imply substituents are less hydrophobic than H
Benzene
(Log P = 2.13)
Chlorobenzene
(Log P = 2.84)
Benzamide
(Log P = 0.64)
Cl CONH2
pCl = 0.71 pCONH = -1.49
2

9. Notes:
•The value of p is only valid for parent structures
•It is possible to calculate log P using p values
•A QSAR equation may include both P and p.
•P measures the importance of a molecule’s overall hydrophobicity (relevant to
absorption, binding etc)
• p identifies specific regions of the molecule which might interact with hydrophobic regions
in the binding site
Hydrophobicity of Substituents
- the substituent hydrophobicity constant (p)
Example:
meta-Chlorobenzamide
Cl
CONH2
Log P(theory) = log P(benzene) + pCl + pCONH
= 2.13 + 0.71 - 1.49
= 1.35
Log P (observed) = 1.51
2

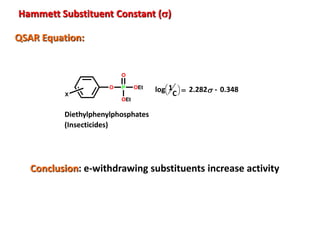
10. Electronic Effects
Hammett Substituent Constant (s)
Notes:
•The constant (s) is a measure of the e-withdrawing or e-donating influence of
substituents
•It can be measured experimentally and tabulated
(e.g. s for aromatic substituents is measured by comparing the
dissociation constants of substituted benzoic acids with
benzoic acid)
X=H K H = Dissociation constant= [PhCO 2-]
[PhCO 2H]
+
CO2H CO2 H
X X

11. +
X = electron
withdrawing
group
X
CO2
CO2H
X
H
X= electron withdrawing group (e.g. NO2)
s X = log
K X
K H
= logK X - logK H
Charge is stabilised by X
Equilibrium shifts to right
KX > KH
Positive value
Hammett Substituent Constant (s)

12. X= electron donating group (e.g. CH3)
s X = log
K X
K H
= logK X - logK H
Charge destabilised
Equilibrium shifts to left
KX < KH
Negative value
Hammett Substituent Constant (s)
+
X = electron
withdrawing
group
X
CO2
CO2H
X
H

13. NOTES:
s value takes into account both inductive and resonance effects
s value depends on whether the substituent is meta or para
ortho values not measured due to steric effect
Hammett Substituent Constant (s)

14. DRUG
N
O
O
meta-Substitution
EXAMPLES: sp (NO2) =0.78 sm (NO2) =0.71
e-withdrawing (inductive effect only)
e-withdrawing
(inductive +
resonance effects)
Hammett Substituent Constant (s)
N
O O
DRUG DRUG
N
O
O
N
O O
DRUG DRUG
N
O
O
para-Substitution

15. sm (OH) =0.12 sp (OH) =-0.37
e-withdrawing (inductive effect only)
e-donating by resonance
more important than
inductive effect
Hammett Substituent Constant (s)
EXAMPLES:
DRUG
OH
meta-Substitution
DRUG
OH
DRUG DRUG
OH OH
DRUG
OH
para-Substitution

16. QSAR Equation:
Diethylphenylphosphates
(Insecticides)
log 1
C



= 2.282s - 0.348
Conclusion: e-withdrawing substituents increase activity
Hammett Substituent Constant (s)
X
O P
O
OEt
OEt

17. Electronic Factors R & F
•R - Quantifies a substituent’s resonance effects
•F - Quantifies a substituent’s inductive effects

18. Steric Factors
Taft’s Steric Factor (Es)
•Measured by comparing the rates of hydrolysis of substituted aliphatic esters
against a standard ester under acidic conditions
Es = log kx - log ko kx represents the rate of hydrolysis of a substituted ester
ko represents the rate of hydrolysis of the parent ester
•Limited to substituents which interact sterically with receptor site
•Cannot be used for substituents which interact with the receptor by resonance or
hydrogen bonding
•May undervalue the steric effect of groups in an intermolecular process (i.e. a
drug binding to a receptor)
•The ‘bulky substituent’ more or less serve as a shield that eventually hinders the
possible and feasible interaction taking place between a ‘drug’ and a ‘receptor’

19. Steric Factors
Molar Refractivity (MR) - a measure of a substituent’s volume
MR =
(n 2
-1)
(n 2
- 2)
x
mol. wt.
density
Correction factor
for polarisation
(n=index of
refraction)
Defines volume
Molar refractivity is specifically significant in a situation when the substituent possesses
either π electron or lone pairs of electrons

20. Hansch Equation
•A QSAR equation relating various physicochemical properties to the biological activity of a
series of compounds
•Usually includes log P, electronic and steric factors
•Start with simple equations and elaborate as more structures are synthesised
•Typical equation for a wide range of log P is parabolic
Log 1
C



= -k (logP) 2 + k 2 logP + k 3 s + k 4 Es + k 5
1

21. Hansch Equation
Log
1
C



 = 1.22 p - 1.59 s + 7.89
Conclusions:
•Activity increases if p is +ve (i.e. hydrophobic substituents)
•Activity increases if s is negative (i.e. e-donating substituents)
Example: Adrenergic blocking activity of b-halo-arylamines
CH CH2 NRR'
X
Y

22. Conclusions:
•Activity increases slightly as log P (hydrophobicity) increases (note that the constant is only
0.14)
•Parabolic equation implies an optimum log Po value for activity
•Activity increases for hydrophobic substituents (esp. ring Y)
•Activity increases for e-withdrawing substituents (esp. ring Y)
Log
1
C



= -0.015 (logP)2 + 0.14 logP + 0.27SpX + 0.40SpY + 0.65 SsX + 0.88SsY + 2.34
Hansch Equation
Example: Antimalarial activity of phenanthrene aminocarbinols (>100 molecules)
X
Y
(HO)HC
CH2NHR'R"

23. QUESTIONS???