Med chem unit2

*
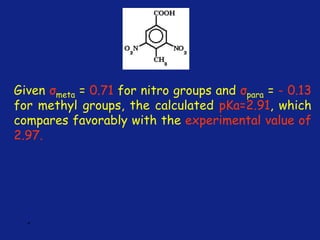
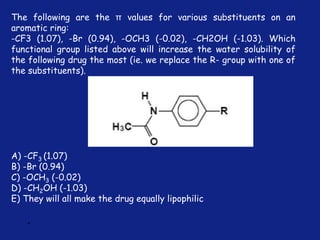
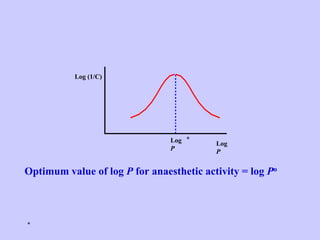
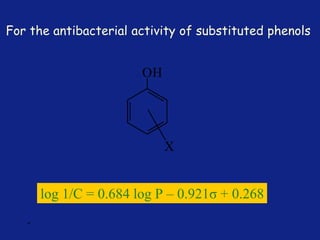
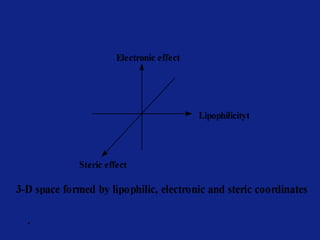
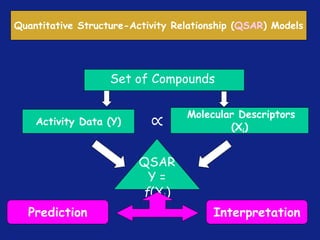
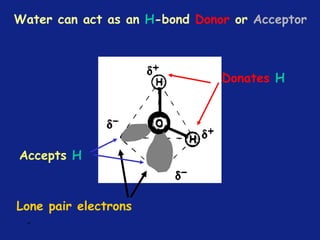
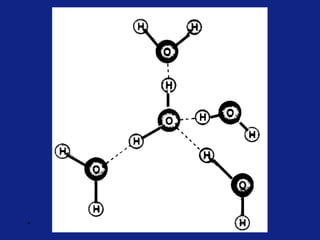
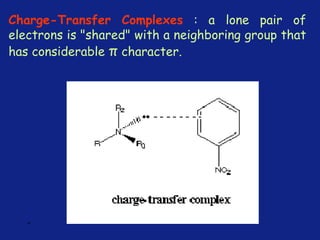
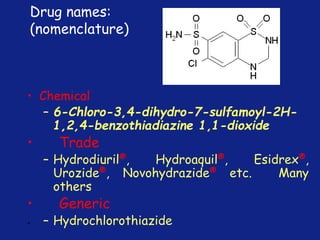
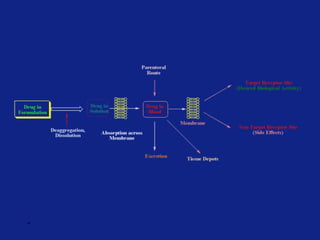
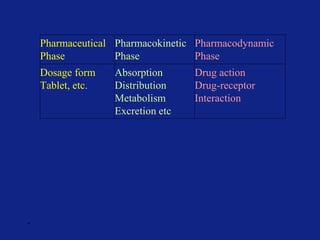
● Medicinal chemistry is a chemistry-based
discipline, also involving aspects of
biological, medical and pharmaceutical
sciences. It is concerned with the invention,
discovery, design, identification and
preparation of biologically active compounds,
the study of their metabolism, the
interpretation of their mode of action at the
molecular level and the construction of
structure-activity relationships (SAR).
● Drugs are strictly defined as chemical
substances that are used to prevent or cure
diseases in human, animals and plants.

*
– The word drug, therefore, imposes an
action-effect context within which the
properties of a substance are described.
For example when a drug is defined as an
analgesic, it means that it is used to
treat pain ….. Thus a drug may described
as having analgesic, vasodepressor,
anticonvulsant, antibacterial, …….…etc
properties.

*
● Drugs activity, solubility in plasma and
distribution to various tissues is dependent
on their physicochemical properties. Even the
interaction of a drug with a receptor or an
enzyme is dependent on characteristics of a
drug molecule, such as ionization, electron
distribution, polarity and electronegativity.
● To understand drug action, the
physicochemical parameters that make
this action possible should be also
understood.

*
Drug names:
(nomenclature)
• Chemical
– 6-Chloro-3,4-dihydro-7-sulfamoyl-2H-
1,2,4-benzothiadiazine 1,1-dioxide
• Trade
– Hydrodiuril®, Hydroaquil®, Esidrex®,
Urozide®, Novohydrazide® etc. Many
others
• Generic
– Hydrochlorothiazide

*
Pharmaceutical
Phase
Pharmacokinetic
Phase
Pharmacodynamic
Phase
Dosage form
Tablet, etc.
Absorption
Distribution
Metabolism
Excretion etc
Drug action
Drug-receptor
Interaction

*
The pH-Partition Hypothesis on Drug Absorption
– This theory provides a basic framework for
understanding of drug absorption from the GIT and
drug transport across the biological membrane. The
principle points of this theory are:
1. The GIT and other biological membranes act as lipid
barriers.
2. The un-ionized form of the acidic or basic drug is
preferentially absorbed.
3. Most drugs are absorbed by passive diffusion.
4. The rate of drug absorption and the amount of drug
absorbed are related to its oil-water partition
coefficient, the more lipophilic the drug, the faster
is its absorption.
5. Weak acidic and neutral drugs may be absorbed
from stomach but basic drugs are not.

*
• Ionization and pH at Absorption site
➢ The fraction of the drug existing in its un-
ionized form in a solution is a function of both the
dissociation constant and the pH of the solution at
the absorption site.
IONIZATION (pKa)

*
➢ It is a means of expressing a drug's solubility is lipid
versus water. A drug is added to a two-phase solution of oil
(or other organic solvent like 1-octanol) and water, mixed,
and the concentration of drug in the organic and water
phases determined. The ratio of the two phases reflects
the relative lipid/water solubility.
Partition Coefficient (Lipid/Water Partition Coefficient)

Lipid-Water Partition Coefficient
– The ratio of the concentration of the
drug in two immiscible phases: a
nonpolar liquid or organic solvent
(representing the membrane); and an
aqueous buffer, pH 7.4 (representing
the plasma)
*

Lipid-Water Partition Coefficient
• The higher the lipid/water p.c. the greater
the rate of transfer across the membrane
– polarity of a drug, by increasing
ionization will the lipid/ water p.c.
– polarity of a drug, suppression of
ionization will the lipid/ water p.c.
*

*
A drug’s partition coefficient, Korg/aqu is an index of the drug’s
lipophilicity.
Log P = 1 means 10:1 Organic:Aqueous
Log P = 0 means 1:1 Organic:Aqueous
Log P = -1 means 1:10 Organic:Aqueous
In general, assuming passive absorption
Optimum CNS penetration around Log P = 2 +/- 0.7
Optimum Oral absorption around Log P = 1.8
Optimum Intestinal absorption Log P =1.35
Optimum Colonic absorption Log P = 1.32
Optimum Sub lingual absorption Log P = 5.5
Optimum Percutaneous Log P = 2.6 (& low mw)

*
– The partition ratio of a given drug will determine
its solubility in plasma, its ability to traverse cell
membranes, and which tissues it will reach.
– Drugs must have some aqueous solubility since this
is essential for absorption through membranes, and
for the production of an adequate concentration at
the site-of-action. A balance between hydrophilicity
and lipohilicity is necessary. This must be taken
into account when chemically modifying a drug for
optimal activity.

*
The relationship between physicochemical
properties and drug action
“Theoretical representations”
➢ Overton-Meyer Hypothesis
o The hypothesis states that, the higher the
partition ratio P, the higher the pharmacological
effect.
➢ The Ferguson Principle
o The concentration of a drug in plasma is directly
proportional to its activity.
o Ferguson Constant is represented by X
where:

*
– High thermodynamic activity means that the
activity of the drug is based on its physicochemical
properties only, such as in a gaseous anesthetic. Such
drugs are known as non-specific agents.

*
– Low thermodynamic activity means that the
activity of the drug is based on its structure
rather than physicochemical properties.
– Agents in this category are called specific
agents, and their activity at low concentrations
infers that they have a specific receptor.

*
Electronic Effects
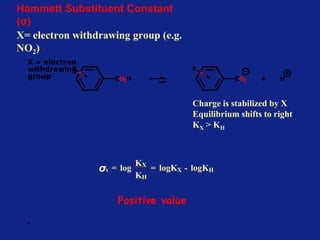
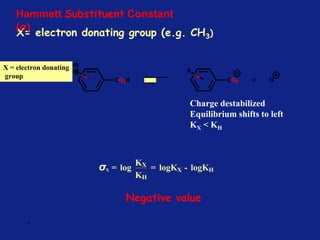
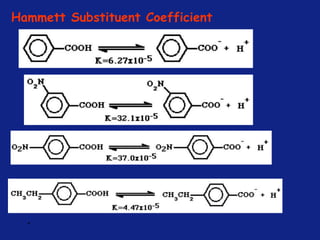
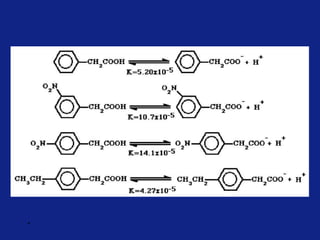
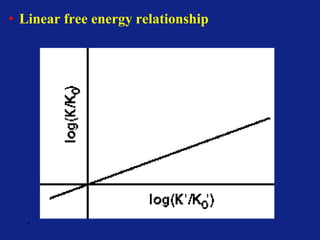
Hammett Substituent Constant
(σ)
• The constant (σ) a measure of the e-withdrawing or e-
donating influence of substituents
• It can be measured experimentally and tabulated
(e.g. s for aromatic substituents is measured by comparing the
dissociation constants of substituted benzoic acids with benzoic
acid)
X=H KH = Dissociation constant= [PhCO2-]
[PhCO2H
]

*
X= electron withdrawing group (e.g.
NO2)
σX = log
KX
KH
= logKX - logKH
Charge is stabilized by X
Equilibrium shifts to right
KX > KH
Positive value
(σ)

*
X= electron donating group (e.g. CH3)
σX = log
KX
KH
= logKX - logKH
Charge destabilized
Equilibrium shifts to left
KX < KH
Negative value
(σ)
X = electron donating
group

*
Hammett Substituent Coefficient

*
σ value depends on inductive and resonance effects
σ value depends on whether the substituent is meta or
para
ortho values are invalid due to steric factors

*
• Linear free energy relationship

*
ρ the slope of the line, is a proportionality
constant pertaining to a given equilibrium.
σ is a descriptor of the substituents (Hammett constant ).
– The magnitude of σ gives the relative strength of
the electron-withdrawing or -donating properties
of the substituents.
• σ is positive if the substituent is electron-
withdrawing and negative if it is electron-donating.

*
Some illustrative values of ρ
Some illustrative values of σ

*
Applications of the Hammett Equation
1. Prediction of the pKa of ionization equilibria.
For benzoic acid derivatives:

*
Given σmeta = 0.71 for nitro groups and σpara = - 0.13
for methyl groups, the calculated pKa=2.91, which
compares favorably with the experimental value of
2.97.

*
2. Selection of the substituents for optimum
biological activity.
e.g. QSAR relating the inhibition of bacterial
growth by a series of sulfonamides
A QSAR was developed based on the σ values of the
substituents
where C is the minimum concentration of compound
that inhibited growth of E. coli.
It was found that electron-withdrawing substituents
favor inhibition of growth.

*
• Hansch derived constants for the
contributions of substituents to the partition
coefficient. The lipophilicity constant, π, is
defined as:
π = log Px - log PH = log (Px/PH)
where Px is partition constant for the compound
with X as substituent and PH is the partition
constant for the parent.
Tables of values of π for other substituents are
available.
Hansch Constant
(π)

*
π values for various substituents
on aromatic rings
CH3 t-Bu OH CONH2 CF3 Cl Br F
0.52 1.68 -0.67 -1.49 1.16 0.71 0.86 0.14
Theoretical Log P for chlorobenzene
= log P for benzene + π for Cl
= 2.13 + 0.71 = 2.84

*
π values for various substituents
on aromatic rings
CH3 t-Bu OH CONH2 CF3 Cl Br F
0.52 1.68 -0.67 -1.49 1.16 0.71 0.86 0.14
Theoretical Log P for meta-chlorobenzamide
= log P for benzene + π for Cl + π for CONH2
= 2.13 + 0.71 - 1.49 = 1.35

*
The following are the π values for various substituents on an
aromatic ring:
-CF3 (1.07), -Br (0.94), -OCH3 (-0.02), -CH2OH (-1.03). Which
functional group listed above will increase the water solubility of
the following drug the most (ie. we replace the R- group with one of
the substituents).
A) -CF3 (1.07)
B) -Br (0.94)
C) -OCH3 (-0.02)
D) -CH2OH (-1.03)
E) They will all make the drug equally lipophilic

*
Steric Effects
➢ The third major factor that often must be
considered in QSAR involves steric effects.
➢ For studies involving reactivity of organic
compounds, a steric parameter, Es, was
defined by Taft as :
where k is the rate constant for the acid
hydrolysis of esters of the type

*
– Assuming the electronic effects of
substituent X can be ignored, the size of X will
affect the transition state and hence the rate
of reaction.
– By definition Es = 0 for X=H.
– Tables of values of Es for other substituents
are available.

*
▪ much harder to quantitate
▪ Examples are:
▪ Taft’s steric factor (Es) (~1956), an
experimental value based on rate constants
▪ Molar refractivity (MR)--measure of the volume
occupied by an atom or group--equation includes
the MW, density, and the index of refraction—
▪ Verloop steric parameter--computer program
uses bond angles, van der Waals radii, bond
lengths
Steric Effects

*
• A drug's activity was really a function of
two processes:
1. its transportation from point of entry to
receptor site(s) (pharmacokinetics).
2. its interaction with the receptor
(pharmacodynamics).
– Hansch proposed that the ability of a drug to
get through a membrane might be modeled by
its partition coefficient between a lipid-type
solvent and water
Hansch Approach

*
The suggested model for a drug traveling
through the body to its receptor site might be:
log 1/C = -k(log P)2 + k'(log P) + k"
where potency is expressed as log (1/C) and C is
the concentration of a drug that provides some
standard biological effect.
➢ This equation has the format for a parabola
➢ The significance of this observation is that an
optimum hydrophobicity may exist.

*
Optimum value of log P for anaesthetic activity = log Po
Log
P
o
Log
P
Log (1/C)

*
– Accordingly several membranes may have to
be traversed for compounds to get to the
target site, and compounds with the greatest
hydrophobicity will become localized in the
membranes they encounter initially, thereby
slowing their transit to the target site.
– Hansch proposed also that there should be a
linear free energy relationship (like the
Hammett equation) between lipophilicity and drug
activity and that this might be indicated by the
partition coefficient

*
Hansch Linear Free Energy Model
• Hansch has derived a general equation based
on linear free-energy considerations.
• In this equation is the ability to incorporate
parameters which encompass the full range of
known biological requirements for drug activity.
• Among theses terms for biological transport,
drug/enzyme binding energies and substituent
effects (both electronic and steric).
• The most general form of Hansch equation is:

*
log 1/C = -aπ2 + bπ + ρσ + c
Where
activity expressed as 1/C, C = concentration,
π is the Hansch constant (measure of lipophilicty),
ρ is constant related to the given molecule,
σ is the Hammett substituent constant which is a
measure of the electronic effect.
Es Taft’s constant
Log 1/C = k1P - k2P2 + k3σ + k4Es +
k5

*
• Look at size and sign for each
component of the equation.
• Values of r <<0.9 indicate equation not
reliable
• Accuracy depends on using enough
analogs, accuracy of data, & choice of
parameters.
Hansch Analysis

*
Examples for Hansch equations
log 1/C = 1.22 π – 1.59 σ + 7.89
(n = 22; r = 0.918)
log 1/C = 0.398 π + 1.089 σ + 1.03 Es + 4.541
(n = 9; r = 0.955)

*
Log
1
C
⎛
⎝
⎞
⎠= 1.22 π - 1.59 σ + 7.89
Conclusions:
• Activity increases if π is + (i.e. hydrophobic substituents)
• Activity increases if σ is negative (i.e. e-donating
substituents)
Examples:
Adrenergic blocking activity of β-halo-β-
arylamines

*
For the antibacterial activity of substituted phenols
log 1/C = 0.684 log P – 0.921σ + 0.268

*
For a series of phosphonate esters, cholinesterase inhibitors
log K = -0.152 π – 1.68 σ + 4.053 Es + 7.212
Where
K is the inhibition constant,
σ is the Hammett substituent constant for
aliphatic systems
Es is the Taft steric constant.
In this example steric effect of the substituents plays an
important role. The bulkier groups cause a decrease in
cholinesterase inhibition.

*
1.For the antibacterial effects on gram-negative bacteria of a series of
diguanidines:
log 1/C = -0.081 π2 + 1.483 π – 1.578

*
Conclusions:
• Activity increases slightly as log P (hydrophobicity) increases
(note that the constant is only 0.14)
• Parabolic equation implies an optimum log Po value for activity
• Activity increases for hydrophobic substituents (esp. ring Y)
• Activity increases for e-withdrawing substituents (esp. ring Y)
Lo
g
1
C
⎛
⎝
⎞
⎠= -0.015
(logP)
2 + 0.14 logP + 0.27ΣπX + 0.40ΣπY + 0.65 ΣσX+ 0.88ΣσY + 2.34
Example: Antimalarial activity of phenanthrene aminocarbinols

*
Quantitative Structure-Activity Relationship (QSAR) Models
Set of Compounds
Activity Data (Y)
Molecular Descriptors
(Xi)∝
QSAR
Y =
f(Xi)
InterpretationPrediction

*
Free-Wilson Analysis
log (1/C) = Σ aixi + μ
xi: presence of group i (0 or 1)
ai: activity group contribution of group i
μ: activity value of unsubstituted compound

*
Dipole-Dipole : Here a partially positive atom in a
dipole is attracted to a partially negative atom in
another dipole.
Hydrogen Bonding : A dipole-dipole interaction
where on of the constituents is a hydrogen
attached to a heteroatom.

*
Hydrogen bonds
– Vary in strength
– Weaker than electrostatic interactions but stronger
than van der Waals interactions
– A hydrogen bond takes place between an electron
deficient hydrogen and an electron rich heteroatom
(N or O)
– The electron deficient hydrogen is usually attached
to a heteroatom (O or N)
– The electron deficient hydrogen is called a hydrogen
bond donor (HBD)
– The electron rich heteroatom is called a hydrogen
bond acceptor (HBA)

*
Hydrogen bonds
HBAHBD
– The interaction involves orbitals and is directional
– Optimum orientation is where the X-H bond points
directly to the lone pair on Y such that the angle
between X, H and Y is 180o

*
Hydrogen bonds
• Examples of strong hydrogen bond acceptors
- carboxylate ion, phosphate ion, tertiary amine
• Examples of moderate hydrogen bond acceptors
- carboxylic acid, amide oxygen, ketone, ester,
ether, alcohol
• Examples of poor hydrogen bond acceptors
- sulfur, fluorine, chlorine, aromatic ring, amide
nitrogen, aromatic amine
• Example of good hydrogen bond donors
- Quaternary ammonium ion

Lone pair electrons
Water can act as an H-bond Donor or Acceptor
Donates H
Accepts H
*

*
Examples of
H-bonding
interactions

*
The Hydrophobic Effect : when two alkyl chains
approach one another, water is extruded from the
space in between them, resulting in an increase in
entropy, and thus a decrease in energy.

*
Charge-Transfer Complexes : a lone pair of
electrons is "shared" with a neighboring group that
has considerable π character.

*
Van der Waals Forces : one carbon in a chain
approaches another carbon on a neighboring chain,
causing a perturbation known as an induced dipole.
These opposite partial charges then attract one
another.

*
➢ Drugs may also bind to receptors using covalent
bonding. This may be a permanent bond, in which
case the receptor or enzyme target is "killed", or
it may be transient.

Med chem unit2

More Related Content

What's hot

Similar to Med chem unit2

More from bvocmithilesh

Recently uploaded

Med chem unit2