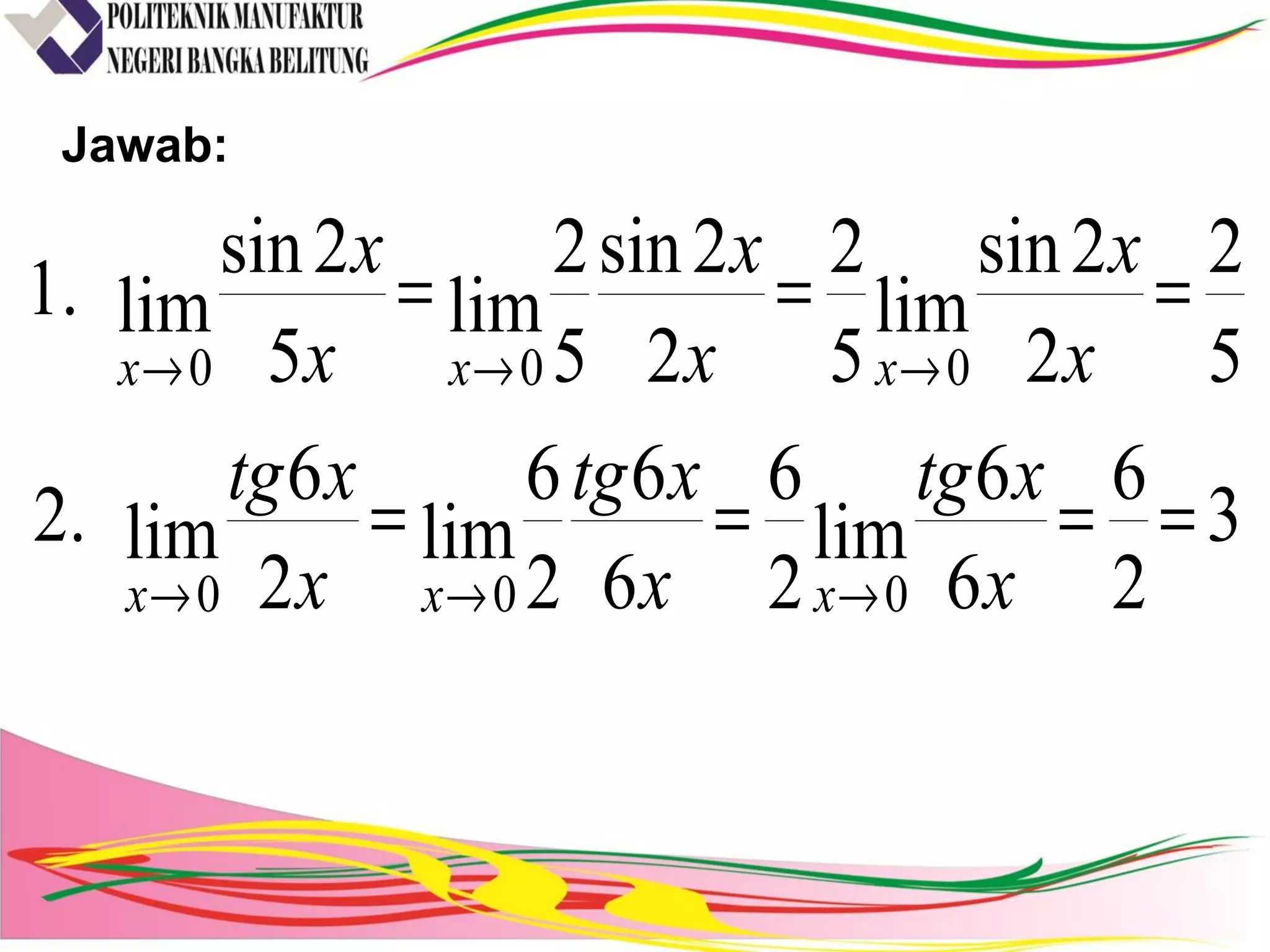1) Dokumen tersebut membahas tentang materi Matematika II khususnya tentang limit fungsi. Dijelaskan definisi dan cara menyelesaikan limit fungsi aljabar dan ketika mendekati tak hingga serta beberapa teorema terkait limit fungsi. 2) Terdapat contoh soal dan penyelesaian mengenai penentuan nilai limit fungsi trigonometri, aljabar, dan ketika mendekati tak hingga. 3) Dibahas pula definisi kontinuitas dan diskontinuit

1. MATEMATIKA II
Oleh:
Dr. Parulian Silalahi, M.Pd
http://polmansem3.esy.es/

2. Limit Fungsi

4. 1. Pengertian Limit
a. Defenisi
= L dapat diartikan bahwa jika x
mendekati a ( tetapi x ≠ a), maka f (x)
mendekati nilai L
b. Cara Menyelesaikan Limit Fungsi Aljabar
a) Substitusi Langsung
b) Dengan cara memfaktorkan
)(lim xf
ax→

5. Cotoh:
Hitunglah nilai limit fungsi-fungsi berikut:
Jawab:
2
)4(
2
)34(.1
2
2
1
lim
lim
−
−
−
→
→
x
x
x
x
x
422)2(
2
)2)(2(
2
)4(
2
131.4)34(.1
limlimlim
lim
22
2
2
1
=+=+=
−
+−
=
−
−
=−=−
→→→
→
x
x
xx
x
x
x
xxx
x

6. 2. Pengertian Limit Fungsi f(x) untuk x
Mendekati Tak- Berhingga
a. Defenisi:
Misalkan fungsi f terdefenisi dalam interval
a ≤ x < ∞ , = L jika dan hanya jika
Untuk tiap bilangan ϵ > 0 didapat bilangan
Positip M, demikian sehingga jika x > M, maka
| f (x) – L | < ϵ
)(lim xf
ax→

7. b. Cara menyelesaikan
1)Membagi dengan pangkat tertinggi
Untuk
Jika m < n maka L = 0
Jika m = n maka L = a/p
Jika m> n maka L = ∞
2) Mengalikan dengan faktor lawan
L
arxqxpx
ccxbxax
nnn
mmm
x
=
++++
++++
−−
−−
∞→ ...
...
21
21
lim

8. Contoh:
1.Hitunglah nilai limit fungsi berikut ini :
865
523
.3
46
752
.2
322
135
.1
26
4
3
24
4
4
lim
lim
lim
+−
−+
+−
−−
+−
−+
∞→
∞→
∞→
xx
xx
xx
xx
xx
xx
x
x
x

9. Jawab:
0
865
523
.3
46
752
.2
2
5
322
135
.1
26
4
3
24
4
4
lim
lim
lim
=
+−
−+
∞=
+−
−−
=
+−
−+
∞→
∞→
∞→
xx
xx
xx
xx
xx
xx
x
x
x

10. 2. Hitunglah nilai limit fungsi berikut:
Jawab
( )12lim +−+
∞→
xx
x
( ) ( ) ( )
( )
( ) ( )
( )
( )
( ) 0
0101
0
11
12
12
12
12
.1212
12
1
lim
lim
limlim
=
+++
=
+++
=
+++
+−+
=
+++
+++
+−+=+−+
∞→
∞→
∞→∞→
xx
x
x
x
xx
xx
xx
xx
xx
xxxx

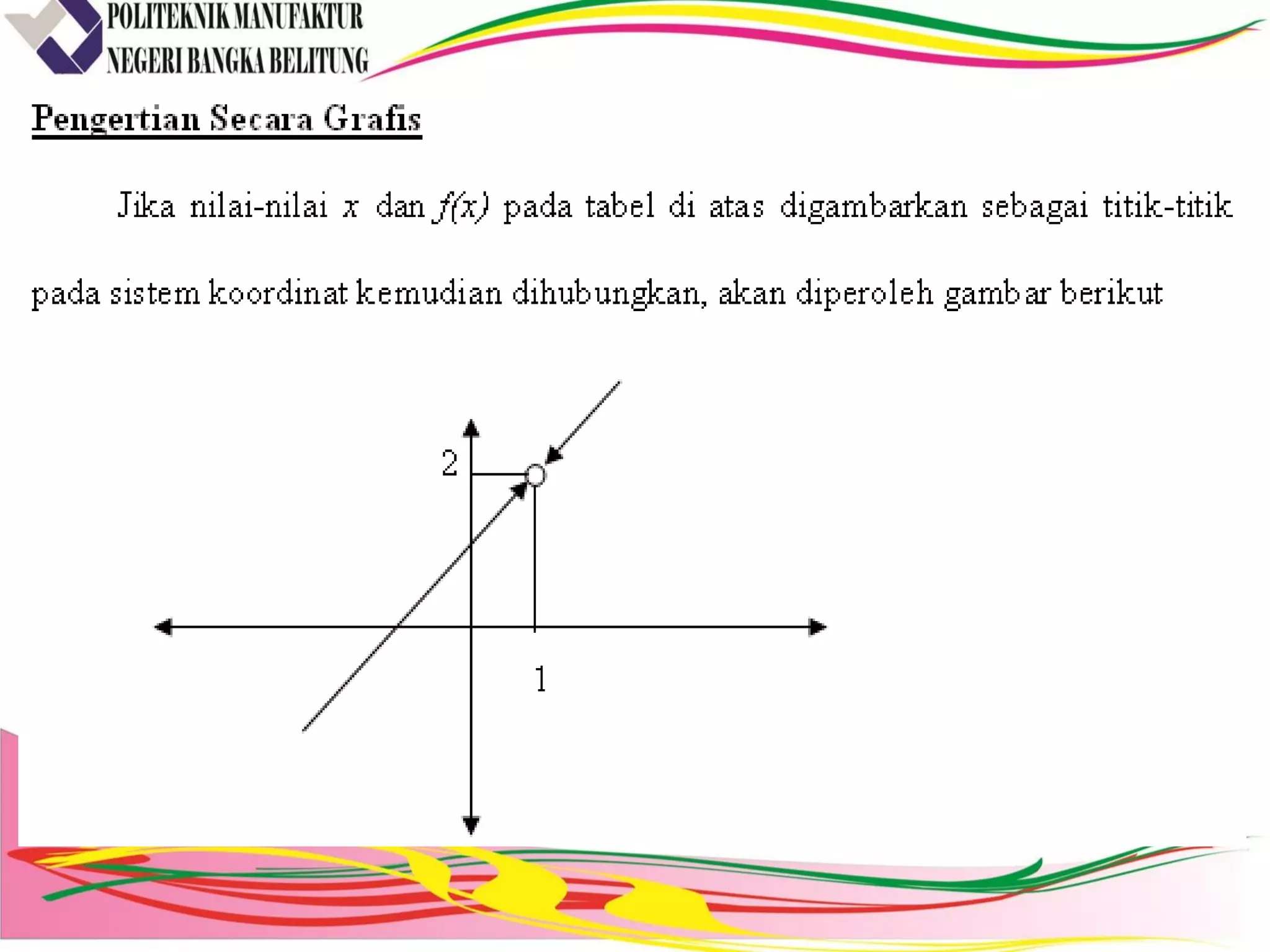
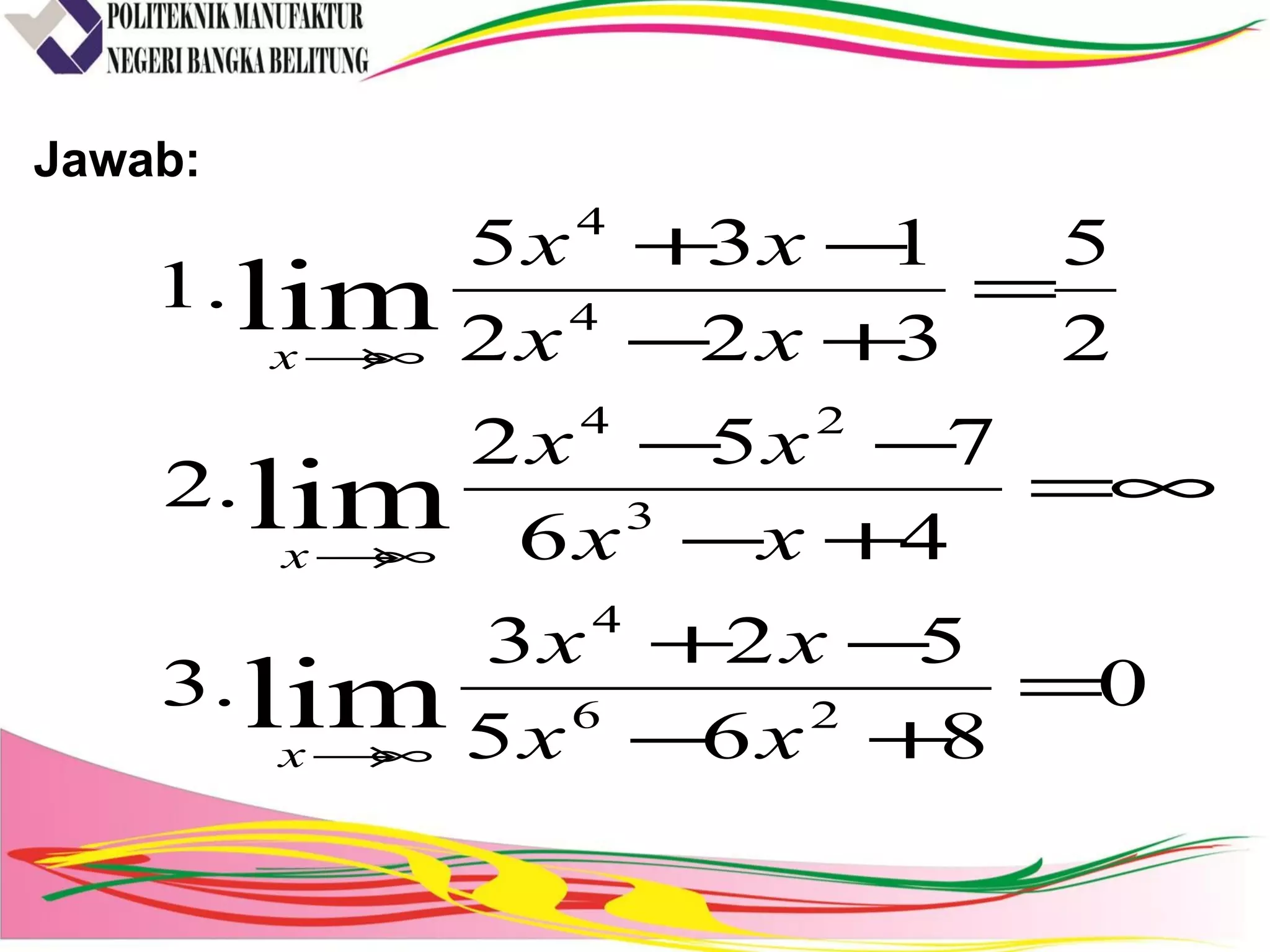
11. 3. Teorema Limit
Beberapa teorema limit yang sering
digunakan untuk menentukan limit fungsi
aljabar.
1.Jika f(x) = k, maka = k
(untuk setiap k konstanta dan a bilangan real)
2. Jika f(x) = x maka = a
(untuk setiap a bilangan real)
3.
)(lim xf
ax→
)(lim xf
ax→
[ ] )()()()( limlimlim xgxfxgxf
axaxax →→→
±=±

12. 4. Jika k konstanta, maka
5.a)
b)
6.a)
b)
)()( limlim xfxkxfxk
axax →→
=
[ ] )().()().( limlimlim xgxfxgxf
axaxax →→→
=
[ ] )(/)()(/)( limlimlim xgxfxgxf
axaxax →→→
=
[ ]
n
ax
n
ax
xfxf 





=
→→
)()( limlim
n
ax
n
ax
xfxf )()( limlim →→
=

13. Contoh:
Hitunglah nilai tiap limit berikut:
1)
2)
Jawab:
1)
)43(lim2
−
→
x
x
x
x
x
52
2
lim
+
→
242.343)43( limlimlim 222
=−=−=−
→→→ xxx
xx

14. 2)
2
3
2
54
2
5
2
)5(5
5
limlim
lim
lim
lim
lim
2
2
2
2
2
2
2
2
2
2
=
+
=
+
=
+
=
+
=
+
→→
→
→
→
→
xx
x
x
x
x
x
x
x
x
x
x

15. 4. Limit Fungsi Trigonometri
Rumus Limit Fungsi Trigonometri
1.
2.
Contoh: Hitunglah nilai limit fungsi berikut:
1limlim
1
sin
lim
sin
lim
00
00
==
==
→→
→→
tgx
x
x
tgx
x
x
x
x
xx
xx
x
xtg
x
x
xx 2
6
lim.2
5
2sin
lim.1
00 →→

16. Jawab:
3
2
6
6
6
lim
2
6
6
6
2
6
lim
2
6
lim.2
5
2
2
2sin
lim
5
2
2
2sin
5
2
lim
5
2sin
lim.1
000
000
====
===
→→→
→→→
x
xtg
x
xtg
x
xtg
x
x
x
x
x
x
xxx
xxx

17. 5. Kontinuitas dan Diskontinuitas Fungsi
Defenisi:
Misalkan fungsi f (x) terdefenisi dalam suatu
interval yang memuat x = a. Fungsi f (x)
dikatakan kontinu di x = a, jika memenuhi tiga
syarat berikut:
1) f(a) harus ada ( a berada dalam domain f(x))
2) Harus ada, dan
3) = f (a)
)(lim xf
ax→
)(lim xf
ax→

18. Contoh:
1.Apakah kontinu di x = 2?
Jawab:
1.
Oleh karena f (2) tidak ada maka
diskontinu di x = 2
2
4
)(
2
−
−
=
x
x
xf
)(
0
0
22
42
)2(
2
adatidakf =
−
−
=
2
4
)(
2
−
−
=
x
x
xf

19. 2. Apakah fungsi f (x) =
Kontinu di x = 1 ?
Jawab:
1)f (1) = 3 f (1) ada
2)





=
≠
−
−
1,
1,
1
1
3
3
xuntuk
xuntuk
x
x
3111)1(lim
1
1
)1)(1(
lim
11
1
lim
1
)(lim
1
22
23
=++=++
→
=
−
++−
→
=
−
−
→
=
→
xx
x
x
xxx
xx
x
x
xf
x

20. 3)
Jadi f(x) kontinu di x = 1
)1()(lim1
fxf
x
=
→

21. TERIMA KASIH
Selamat Belajar