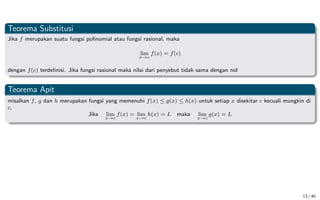
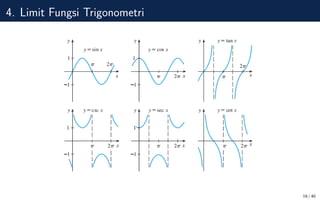
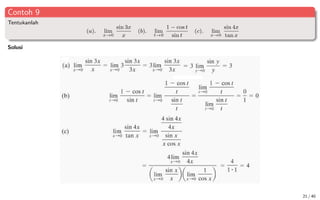
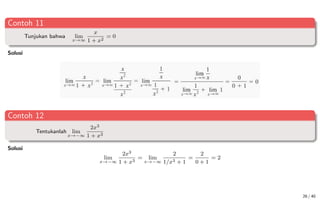
Dokumen ini membahas mengenai konsep limit dalam kalkulus, mencakup definisi formal, teorema, dan contoh penerapan limit pada fungsi trigonometri serta limit di tak hingga. Selain itu, dijelaskan juga tentang kekontinuan fungsi dan penyebab terjadinya diskontinuitas. Dokumen ini berisi teori dan analisis matematis mendalam serta latihan untuk pemahaman lebih lanjut.

1. KALKULUS I
LIMIT
Mia Siti Khumaeroh, M.Si
Jurusan Matematika
Fakultas Sains dan Teknologi
UIN Sunan Gunung Djati Bandung
1 / 40

2. OUTLINE
• LIMIT
1. Pendahuluan Limit
2. Definisi Formal Limit
3. Teorema Limit
4. Limit Fungsi Trigonometri
5. Limit Takhingga dan Limit di Takhingga
6. Kekontinuan Fungsi
• Referensi
Edwin J. Purcell, Dale Varberg Steven E. Rigdon, Calculus, Ninth Edition
2 / 40

3. 1. Pendahuluan Limit
3 / 40

4. 1. Pendahuluan Limit
• Perhatikan fungsi berikut
f(x) =
x3 − 1
x − 1
Fungsi tidak terdefinisi di x = 1 karena f(x)
mempunyai bentuk 0
0
.
• Apa yang terjadi pada f(x) saat x mendekati 1?
• Secara matematis ditulis
lim
x→1
x3 − 1
x − 1
= 3
4 / 40

5. Definisi limit secara intuitif
lim
x→c
f(x) = L, menyatakan bahwa pada saat x dekat namun berbeda dengan c maka f(x) dekat dengan L
lim
x→c−
f(x) = L, menyatakan bahwa pada saat x dekat namun dari arah kiri c maka f(x) dekat dengan L
lim
x→c+
f(x) = L, menyatakan bahwa pada saat x dekat namun dari arah kanan c maka f(x) dekat dengan L
lim
x→c
f(x) = L, jika dan hanya jika lim
x→c−
f(x) = L dan lim
x→c+
f(x) = L
5 / 40

6. Contoh 1
Tentukanlah (a). lim
x→2
(4x − 3) (b). lim
x→3
x2 − x − 6
x − 3
(c). lim
x→0
sin x
x
Jawab
(a). lim
x→2
(4x − 3) = 4(2) − 3 = 5
(b). lim
x→3
x2 − x − 6
x − 3
= lim
x→3
(x − 3)(x + 2)
x − 3
= lim
x→3
(x + 2) = 5
(c). lim
x→0
sin x
x
= 1
6 / 40

7. Contoh 2
Tentukan lim
x→0
sin
1
x
lim
x→0
sin
1
x
tidak ada
Contoh 3
7 / 40

8. 2. Definisi Formal Limit
8 / 40

9. 2. Definisi Formal Limit
Definisi
Dikatakan limx→c f(x) = L, jika untuk setiap 0 yang diberikan (sekecil apapun nilainya), terdapat δ 0 yang
bersesuaian sehingga |f(x) − L| pada saat 0 |x − c| δ
atau
0 |x − c| δ → |f(x) − L|
9 / 40

10. Contoh 4
Buktikan bahwa limx→4(3x − 7) = 5
Jawab
Analisis Pendahuluan
Misalkan merupakan sebarang bilangan bulat positif. Maka akan dicari δ 0 sehingga
0 |x − 4| δ → |(3x − 7) − 5|
Pandang pertaksamaan pada bagian kanan
sehingga dapat dipilih δ =
3
Bukti Formal
Untuk setiap yang diberikan, pilih δ = /3, sehingga untuk 0 |x − 4| δ akan diperoleh
|(3x − 7) − 5| = |3x − 12| = |3||x − 4| 3δ =
maka terbukti |(3x − 7) − 5|
10 / 40

11. 3. Teorema Limit
11 / 40

12. 3. Teorema Limit
Teorema A
Misalkan n merupakan bilangan bulat positif, k Konstanta, f dan g merupakan fungsi yang mempunyai nilai limit di c,
maka :
1. lim
x→c
k = k
2. lim
x→c
x = c
3. lim
x→c
kf(x) = k lim
x→c
f(x)
4. lim
x→c
[f(x) + g(x)] = lim
x→c
f(x) + lim
x→c
g(x)
5. lim
x→c
[f(x) − g(x)] = lim
x→c
f(x) − lim
x→c
g(x)
6. lim
x→c
[f(x) · g(x)] = lim
x→c
f(x) · lim
x→c
g(x)
7. lim
x→c
f(x)
g(x)
=
limx→c f(x)
limx→c g(x)
, dengan lim
x→c
g(x) 6= 0
8. lim
x→c
[f(x)]n
= [ lim
x→c
f(x)]n
9. lim
x→c
n
p
f(x) = n
q
lim
x→c
f(x) dengan lim
x→c
f(x) ≥ 0 pada saat n genap
12 / 40

13. Teorema Substitusi
Jika f merupakan suatu fungsi polinomial atau fungsi rasional, maka
lim
x→c
f(x) = f(c)
dengan f(c) terdefinisi. Jika fungsi rasional maka nilai dari penyebut tidak sama dengan nol
Teorema Apit
misalkan f, g dan h merupakan fungsi yang memenuhi f(x) ≤ g(x) ≤ h(x) untuk setiap x disekitar c kecuali mungkin di
c,
Jika lim
x→c
f(x) = lim
x→c
h(x) = L maka lim
x→c
g(x) = L
13 / 40

14. Contoh 5
Tentukanlah (a). lim
x→3
2x4
(b). lim
x→4
(3x2
− 2x)
Jawab
14 / 40

15. Contoh 6
Tentukanlah (a). lim
xto2
7x5 − 10x4 − 13x + 6
3x2 − 6x − 8
(b) lim
x→1
x3 + 3x + 7
x2 − 2x + 1
Jawab
(a). lim
x→2
7x5 − 10x4 − 13x + 6
3x2 − 6x − 8
=
7(2)5 − 10(2)4 − 13(2) + 6
3(2)2 − 6(2) − 8
= −
11
2
(b). lim
x→1
x3 + 3x + 7
x2 − 2x + 1
= lim
x→1
x3 + 3x + 7
(x − 1)2
Metode substitusi tidak dapat digunakan
15 / 40

16. Contoh 7
Asumsikan telah dibuktikan bahwa 1 − x2
6
≤ sin x
x
≤ 1 untuk x yang dekat ke 0 tapi tidak sama dengan 0, berapakah
limx→0
sin x
x
?
Jawab
Misalkan f(x) = 1 − x2
6
, g(x) = sin x
x
, dan h(x) = 1, diketahui bahwa
lim
x→0
f(x) = lim
x→0
h(x) = 1
maka dengan menggunakan teorema apit diperoleh
lim
x→0
sin x
x
= 1
16 / 40

17. 4. Limit Fungsi Trigonometri
17 / 40

18. 4. Limit Fungsi Trigonometri
Teorema A. Limit Fungsi Trigonometri
Untuk setiap bilangan real c pada domain dari fungsi,
(1). lim
t→c
sin t = sin c (2). lim
t→c
cos t = cos c
(3). lim
t→c
tan t = tan c (4). lim
t→c
cot t = cot c
(5). lim
t→c
sec t = sec c (6). lim
t→c
csc t = csc c
Teorema B. Limit Khusus Trigonometri
(a). lim
t→0
sin t
t
= 1 (b). lim
t→0
1 − cos t
t
= 0
18 / 40

19. 4. Limit Fungsi Trigonometri
19 / 40

20. Contoh 8
Tentukanlah lim
t→0
t2 cos t
t + 1
Solusi
lim
t→0
t2 cos t
t + 1
= lim
t→0
t2
t + 1
( cos t) =
02
0 + 1
· cos 0 = 0 · 1 = 0
20 / 40

21. Contoh 9
Tentukanlah
(a). lim
x→0
sin 3x
x
(b). lim
t→0
1 − cos t
sin t
(c). lim
x→0
sin 4x
tan x
Solusi
21 / 40

22. 5. Limit di Takhingga dan Limit Takhingga
22 / 40

23. 5. Limit di Takhingga dan Limit Takhingga
A. Limit di Takhingga
Definisi 1
Misalkan f suatu fungsi yang terdefinisi pada interval (a, ∞), maka
lim
x→∞
f(x) = L
menyatakan bahwa nilai f(x) dapat dibuat sedemikian dekat dengan L dengan mengambil nilai x cukup basar.
23 / 40

24. Definisi 2
Misalkan f suatu fungsi yang terdefinisi pada interval (−∞, a), maka
lim
x→−∞
f(x) = L
menyatakan bahwa nilai f(x) dapat dibuat sedemikian dekat dengan L dengan mengambil nilai x negatif cukup basar.
Garis y = L disebut sebagai Asimtot Horizontal/Asimtot Datar dari kurva y = f(x) jika
lim
x→∞
f(x) = L atau lim
x→−∞
f(x) = L
24 / 40

25. Aturan limit di Takhingga
lim
x→∞
1
xk
= 0 untuk sebarang k 0
Contoh 10
Tentukan limx→∞
1
x
dan limx→−∞
1
x
Solusi.
Perhatikan bahwa pada saat nilai x membesar, nilai fungsi 1
x
semakin kecil menuju 0
1
100
= 0.01
1
10000
= 0.0001
1
1000000
= 0.000001
Semakin besar x baik ke arah positif maupun negatif, nilai 1/x mendekati 0. Sehingga
lim
x→∞
1
x
= 0 dan lim
x→−∞
1
x
= 0
Garis y = 0 merupakan asimtot datar dari fungsi f(x) = 1/x.
25 / 40

26. Contoh 11
Tunjukan bahwa lim
x→∞
x
1 + x2
= 0
Solusi
Contoh 12
Tentukanlah lim
x→−∞
2x3
1 + x3
Solusi
lim
x→−∞
2x3
1 + x3
= lim
x→−∞
2
1/x3 + 1
=
2
0 + 1
= 2
26 / 40

27. B. Limit Takhingga
Definisi
Misalkan f merupakan suatu fungsi yang terdefinisi disekitar a, kecuali mungkin di a,
lim
x→a
f(x) = ∞
menyatakan bahwa nilai f(x) dapat dibuat sedemikian besar dengan mengambil x yang cukup dekat ke a tapi tidak sama
dengn a.
Garis x = a disebut sebagai asimptot vertikal/asimptot tegak dari y = f(x) jika mamanuhi paling sedikit satu persamaan
berikut
lim
x→a
f(x) = ∞ lim
x→a−
f(x) = ∞ lim
x→a+
f(x) = ∞
lim
x→a
f(x) = −∞ lim
x→a−
f(x) = −∞ lim
x→a+
f(x) = −∞
27 / 40

28. 28 / 40

29. Contoh 13
Tentukan nilai lim
x→1−
1
(x − 1)2
dan lim
x→1+
1
(x − 1)2
Solusi.
• Saat x semakin dekat ke 1 dari kiri (1−), pembilang tetap 1 dan penyebut (1 − x)2 akan semakin dekat ke 0,
sehingga fungsi 1/(1 − x)2 akan membesar dan positif
• Saat x semakin dekat ke 1 dari kanan (1+), pembilang tetap 1 dan penyebut (1 − x)2 akan semakin dekat ke 0,
sehingga fungsi 1/(1 − x)2 akan membesar dan positif
29 / 40

30. Contoh 14
Tentukan lim
x→3+
2x
x − 3
dan lim
x→3−
2x
x − 3
Solusi.
• Jika x menuju 3 dari kiri (3−), bagian pembilang 2x dekat ke 6 dan penyebut x − 3 menuju nol dan negatif .
Sehingga
lim
x→3−
2x
x − 3
= −∞
• Jika x menuju 3 dari kanan (3+), bagian pembilang 2x dekat ke 6 dan penyebut x − 3 menuju nol dan positif .
Sehingga
lim
x→3+
2x
x − 3
= +∞
30 / 40

31. Contoh 15
Tentukan nilai lim
x→2+
x + 1
(x2 − 5x + 6)
Solusi
lim
x→2+
x + 1
x2 − 5x + 6
= lim
x→2+
x + 1
(x − 2)(x − 3)
• Pada bagian pembilang pada saat x → 2+, maka (x + 1) → 3
• Pada bagian penyebut pada saat x → 2+, maka (x − 2) → 0+ dan (x − 3) → −1
Sehingga
lim
x→2+
x + 1
(x − 2)(x − 3)
= −∞
31 / 40

32. 6. Kekontinuan Fungsi
32 / 40

33. 6. Kekontinuan Fungsi
Definisi
Misalkan f adalah fungsi yang terdefinisi pada selang yang memuat c, maka f(x) kontinu di c jika
lim
x→c
f(x) = f(c)
Kenontinuan fungsi harus memenuhi 3 syarat berikut
1. lim
x→c
f(x) ada
2. f(c) ada, (c terdapat dalam domain f)
3. lim
x→c
f(x) = f(c)
33 / 40

34. Contoh 16
Perhatikan grafik fungsi berikut ini, tentukan dimana fungsi tidak kontinu.
Solusi
• Fungsi tidak kontinu di x = 1 karena tidak terdapat nilai fungsi di x = 1 atau f(1) tidak ada
• Fungsi tidak kontinu di x = 3 karena nilai limit kiri dan limit kanan dari fungsi di x = 1 berbeda, sehingga nilai limit
fungsinya tidak ada.
• Fungsi tidak kontinu di x = 5 karena nilai limit tidak sama dengan nilai fungsinya
lim
x→f
f(x) 6= f(5)
34 / 40

35. Contoh 17
Tentukanlah apakah fungsi-fungsi berikut kontinu
35 / 40

36. Solusi
(a). Fungsi f(x) tidak terdefinisi di x = 2 (penyebut tidak boleh nol) atau f(2) tidak ada, sehingga fungsi f diskoninu
di x = 2
(b). Diketahui g(0) = 1, namun
lim
x→0
g(x) = lim
x→0
1
x2
= ∞
Sehingga fungsi g(x) diskontinu di x = 0
(c). Diketahui h(2) = 2,
lim
x→2
h(x) = lim
x→2
x2 − x − 2
x − 2
= lim
x→2
(x − 2)(x + 1)
x − 2
= lim
x→2
(x + 1) = 3
maka
lim
x→2
h(x) 6= h(2)
Sehingga fungsi h diskontinu di x = 2.
(d). Diketahui
lim
t→0−
H(t) = 0 lim
t→0+
H(t) = 1
limit kiri dan kanan dari fungsi H berbeda, sehingga fungsi H tidak memiliki nilai limit di x = 0, Dengan demikian
fungsi H diskontinu karena tidak memiliki nilai limit.
36 / 40

37. 37 / 40

38. LATIHAN
38 / 40

39. LATIHAN
1. Tentukan nilai limit pada gambar berikut, nyatakan jika limitnya tidak ada
2. Tentukan nilai limit berikut atau nyatakan jika limitnya tidak ada
3. Tentukan nilai limit fungsi di takhingga berikut
39 / 40

40. LATIHAN
4. Tentukan nilai limit berikut
5. Tentukan apakah fungsi berikut kontinu di x = 3
40 / 40