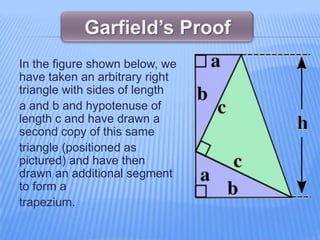
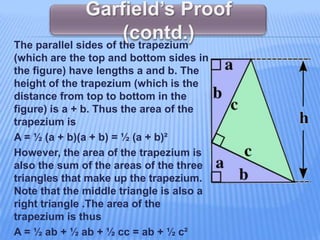
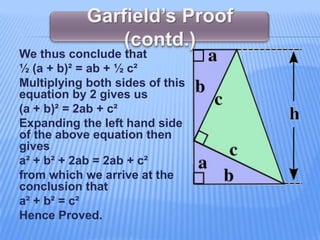
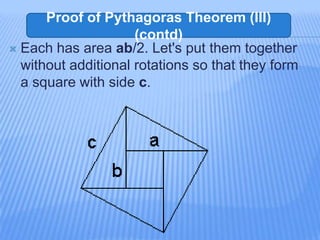
The document discusses several proofs of the Pythagorean theorem provided by different mathematicians. It begins by stating the theorem, then provides 6 different proofs: the first given by President James Garfield in 1876 using a trapezoid approach; the second using similarity of triangles; the third constructing a square from 4 copies of a right triangle; the fourth also using similarity; the fifth by rearrangement of the formula; and the sixth using a geometric representation of the areas. It also discusses some applications of the theorem in fields like architecture, navigation, and coordinate geometry.

2. In mathematics, the Pythagorean
theorem or Pythagoras' theorem is a relation
in Euclidean geometry among the three sides of
a right triangle (right-angled triangle). It states that
:
In any right-angled triangle, the Square of the
Hypotenuse of a Right Angled Triangle Is Equal To
The Sum of Squares of the Other Two Sides.

3.  The twentieth president of the United States
gave the following proof to the Pythagoras
Theorem. He discovered this proof five years
before he became President. He hit upon this
proof in 1876 during a mathematics
discussion with some of the members of
Congress. It was later published in the New
England Journal of Education.

4. In the figure shown below, we
have taken an arbitrary right
triangle with sides of length
a and b and hypotenuse of
length c and have drawn a
second copy of this same
triangle (positioned as
pictured) and have then
drawn an additional segment
to form a
trapezium.

5. The parallel sides of the trapezium
(which are the top and bottom sides in
the figure) have lengths a and b. The
height of the trapezium (which is the
distance from top to bottom in the
figure) is a + b. Thus the area of the
trapezium is
A = ½ (a + b)(a + b) = ½ (a + b)²
However, the area of the trapezium is
also the sum of the areas of the three
triangles that make up the trapezium.
Note that the middle triangle is also a
right triangle .The area of the
trapezium is thus
A = ½ ab + ½ ab + ½ cc = ab + ½ c²

6. We thus conclude that
½ (a + b)² = ab + ½ c²
Multiplying both sides of this
equation by 2 gives us
(a + b)² = 2ab + c²
Expanding the left hand side
of the above equation then
gives
a² + b² + 2ab = 2ab + c²
from which we arrive at the
conclusion that
a² + b² = c²
Hence Proved.

7. y
In the figure, ∆ACB is a right angle E D
triangle, with angle ACB = 90 ⁰ with
hypotenuse c c
To prove: a² + b² = c² x
Construction: Extend AC to D such that A
AD = AB = c. c
b
Draw ED perpendicular to CD with ED = y
Draw AE as the angle bisector of angle BAD. F u B a C
Let EB and EA meet at E.
Draw EF perpendicular to CF with EF = x.
Proof: In ∆EAD and ∆EAB,
AD = AB (by construction)
Angle EAD = angle EAB (AE bisects
angle BAD)
EA is common
So, by SAS property ∆EAD is congruent to
∆EAB = EB = y (by CPCTE)
and ED
So, angle ADE = angle ABE = 90⁰ (by
CPCTE)

8. Now, angle EBF + angle EBA + angle ABC = y
E D
180⁰
i.e. angle EBF + angle ABC = 90⁰
c
Also, in ∆EFB,
angle EBF + angle BEF = 90⁰ x y A
So, angle ABC = angle BEF c
b
In ∆ACB and ∆BFE, F u B a C
angle ABC = angle BEF
angle ACB = angle BFE = 90⁰
So, by AA similarity ∆ACB is similar to ∆BFE
Thus, AC/BF = CB/FE = AB/BE
i.e. b/u = a/x = c/y
This implies u = bx/a = b(b+c)/a --------(1)
and y = cx/a = c(b+c)/a --------(2)
but y = u+a (as EFCD is a rectangle) ----
-(3)
So, by using (2), c(b+c)/a = u+a
Using (1) we get, c(b+c)/a = b(b+c)/a + a
which on simplifying gives a² + b² = c².

9. Proof of Pythagoras Theorem (III)
 We start with four copies of the same
triangle. Three of these have been rotated
90°, 180°, and 270°, respectively.

10. Proof of Pythagoras Theorem (III)
(contd)
 Each has area ab/2. Let's put them together
without additional rotations so that they form
a square with side c.

11. Proof of Pythagoras Theorem (III)
(contd)
 The square has a square hole with the
side (a - b). Summing up its area (a - b)² and
2ab, the area of the four triangles
(4·ab/2), we get
 C²=(a-b)²+2ab
 C²= a²+b² -2ab+2ab
 C²=a²+b²
 Hence Proved.

12. Pythagoras Theorem Proof (Through
Similarity) (IV)
Theorem: In a right triangle, the square of the hypotenuse is
equal to the sum of the squares of the other two sides.
Given: A right-angled triangle with angle A = 90*

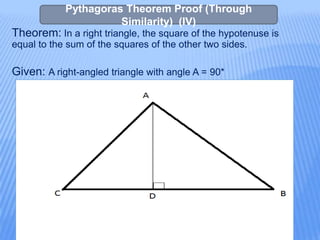
13. Pythagoras Theorem Proof (Through Similarity) (IV)
(contd.)
To Prove: (Hypotenuse)2 = (Base) 2 + (Perpendicular) 2
Construction: From A draw AD perpendicular to BC
Proof: In triangles ADC and BAC,
(i) angle ADC = angle BAC [both
90*]
(ii) angle C = angle C
[common]
By AA similarity criterion,
Triangle ADC is similar to BAC.
Since corresponding sides are proportional in similar triangles,
CD/AC = AC/BC
AC2 = CD X BC
(a)
In triangles ADB and BAC,
(i) angle BDA = angle BAC [both 90*]

14. Pythagoras Theorem Proof (Through Similarity) (IV)
(contd.)
So, By AA similarity criterion,
Triangle ADB is similar to BAC.
BD/AB = AB/BC
AB 2 = BC X BD (b)
Adding (a) and (b),
AB 2 + AC 2 = CD X BC + BC X BD
AB 2 + AC 2 = BC( CD + BD)
AB 2 + AC 2 = BC(BC)
AB 2 + AC 2 = BC 2
Hence Proved

15. PROOF BY REARRANGEMENT (V)

16. PROOF BY REARRANGEMENT (V) (CONTD)

17. PYTHAGORAS THEOREM PROOF (VI)
"The square on the hypotenuse of a right triangle is equal to the sum of
the squares on the two legs" (Eves 80-81).
This theorem is talking about the area of the squares that are built on each side
of the right triangle
Accordingly, we obtain the following areas for the squares, where the
green and blue squares are on the legs of the right triangle and the red
square is on the hypotenuse.
area of the green square is
area of the blue square is
area of the red square is
From our theorem, we have the following
relationship:
area of green square + area of blue square = area of red square or
As I stated earlier, this theorem was named after Pythagoras because he was the first to
prove it. He probably used a dissection type of proof similar to the following in proving
this theorem.

18. Some real life uses of Pythagoras
Theorem
Architectureand
Construction
Navigation
Earthquake Location
Crime Scene Investigation
Arrow or Missile Trajectory

19. Pythagoras theorem is used in Coordinate Geometry. It is used in finding
the Euclidean distance formula d = (x₂ - x₁)² + (y₂ - y₁)²
(x₁, y₁)
d² = a² + b²
= (x₂ - x₁)² + (y₂ - y₁)² d = distance
d = (x₂ - x₁)² + (y₂ - y₁)² b= y₂ -
y₁
(x₂, y₂)
a = x₂ - x₁

20.  One of the Pythagorean triplet is a multiple of 3
 One of the Pythagorean triplet is a multiple of 4
 One of the Pythagorean triplet is a multiple of 5
Some examples:
(3,4,5) (5,12,13) (7,24,25)
(8,15,17) (9,40,41) (11,60,61)
(12,35,37) (13,84,85) (16,63,65)
 If you multiply each member of the Pythagorean triplet by n, where n is
a positive real number then, the resulting set is another Pythagorean
triplet
For example, (3,4,5) and (6,8,10) are Pythagorean triplets.
The only fundamental Pythagorean triangle whose area is twice its
perimeter is (9, 40, 41).

21. APPLICATIONS OF CONVERSE OF
PYTHAGORAS THEOREM
The converse of Pythagoras theorem can be used to
categorize triangles
If a² + b² = c² , then triangle ABC is a right angled triangle
If a² + b² < c² , then triangle ABC is an obtuse angled triangle
If a² + b² > c² , then triangle ABC is an acute angled triangle