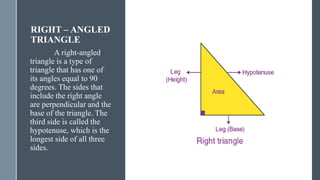
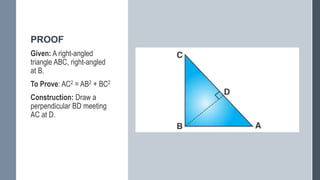
The document explains Pythagoras theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. It provides the definition of a right-angled triangle, the formula for the theorem, and a proof of the theorem. It also discusses applications of the theorem such as determining if a triangle is right-angled or calculating an unknown side of a right triangle.

1. PYTHAGORAS THEOREM
Your best friend to solve Right-angled
triangles.
Presented by
Vaishika G
1020721BD143

2. Overview
› Pythagoras Theorem (also called Pythagorean Theorem) is an
important topic in Mathematics, which explains the relation
between the sides of a right-angled triangle.
› Pythagoras theorem is basically used to find the length of an
unknown side and the angle of a triangle.
› By this theorem, we can derive the base, perpendicular and
hypotenuse formulas.
› The sides of the right triangle are also called Pythagorean triples.

3. RIGHT – ANGLED
TRIANGLE
A right-angled
triangle is a type of
triangle that has one of
its angles equal to 90
degrees. The sides that
include the right angle
are perpendicular and the
base of the triangle. The
third side is called the
hypotenuse, which is the
longest side of all three
sides.

4. Statement
Pythagoras theorem states that “In a right-angled
triangle, the square of the hypotenuse side is equal to the sum
of squares of the other two sides“.

5. Formula
Consider the triangle given in the previous slide:
Where “a” is the perpendicular,
“b” is the base,
“c” is the hypotenuse.
According to the definition, the Pythagoras Theorem formula is
given as:
2

6. PROOF
Given: A right-angled
triangle ABC, right-angled
at B.
To Prove: AC2 = AB2 + BC2
Construction: Draw a
perpendicular BD meeting
AC at D.

7. Proof
› We know, △ADB ~ △ABC
› Therefore,
›
𝐴𝐷
𝐴𝐵
=
𝐴𝐵
𝐴𝐶
(corresponding sides of similar triangles)
› Or, AB2 = AD × AC ……………………………..……..(1)
› Also, △BDC ~△ABC
› Therefore,
›
𝐶𝐷
𝐵𝐶
=
𝐵𝐶
𝐴𝐶

8. Proof
› Or, BC2= CD × AC ……………………………………..(2)
› Adding the equations (1) and (2) we get,
› AB2 + BC2 = AD × AC + CD × AC
› AB2 + BC2 = AC (AD + CD)
› Since, AD + CD = AC
› Therefore, AC2 = AB2 + BC2
› Hence, the Pythagorean theorem is proved.

9. Application
• To know if the triangle is a right-angled triangle or not.
• In a right-angled triangle, we can calculate the length of any side if the
other two sides are given.
• To find the diagonal of a square.

10. Wrapping it up
 The Pythagorean Theorem
can be used only on
_____triangles.
 When should the
Pythagorean Theorem be
used?
 What should be done first
when solving a word problem
involving the Pythagorean
Theorem?
 What must be done before
writing the answer to a
Pythagorean Theorem
problem?
 Right
 When the length of 2 sides
are known and the length of
3rd side is needed
 Draw and label triangle
 Check to see whether the
answer should be rounded or
not