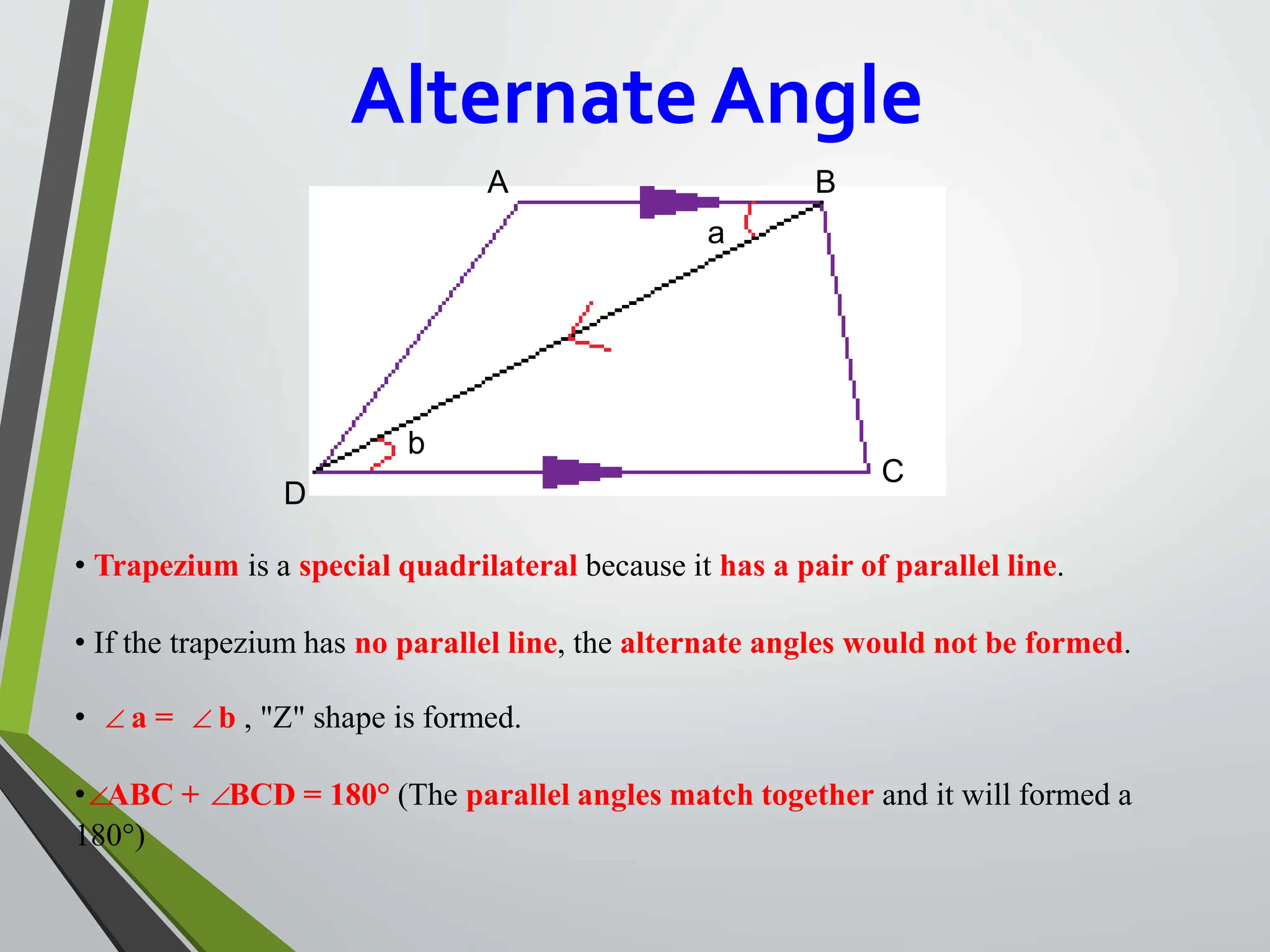
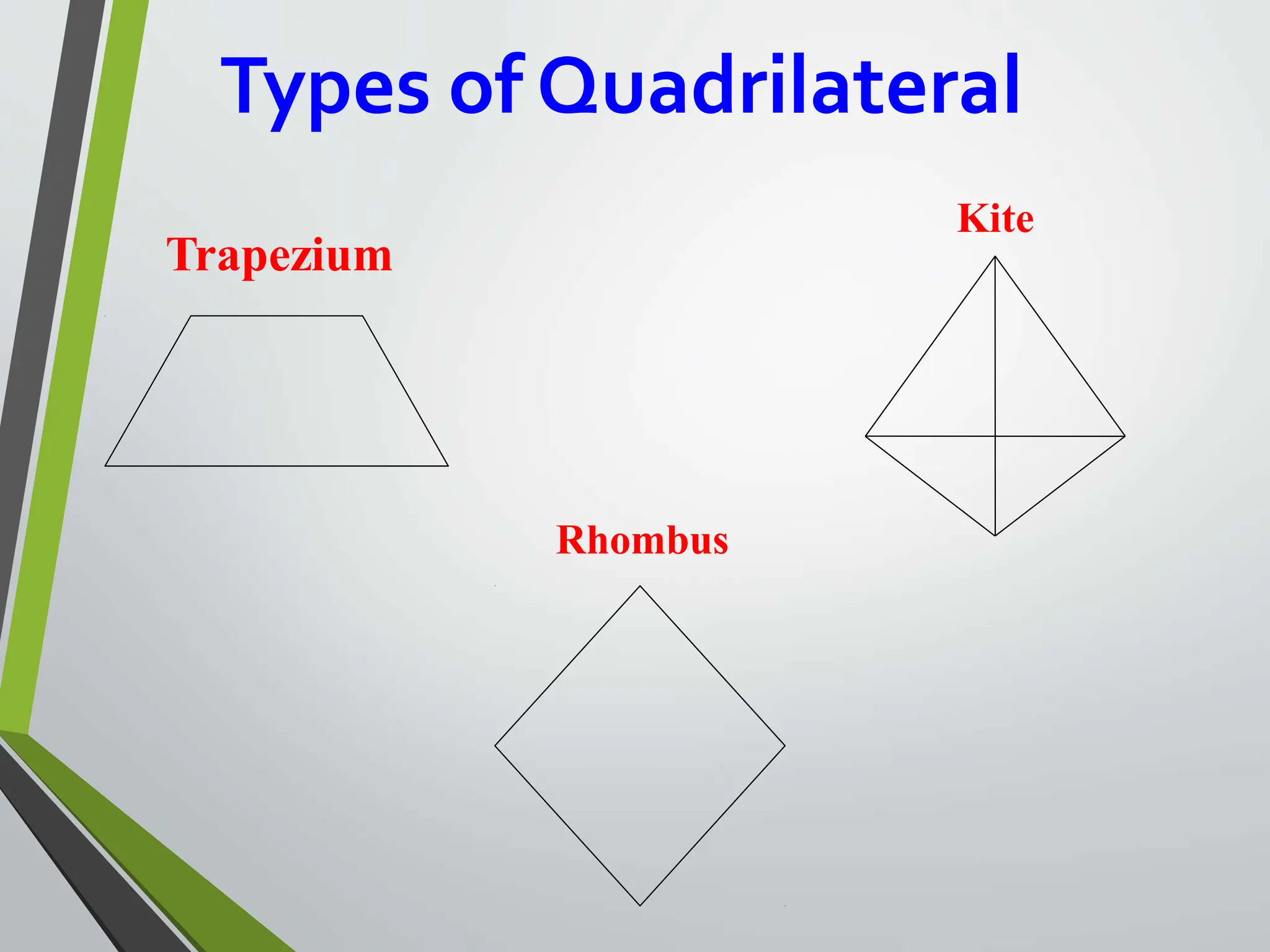
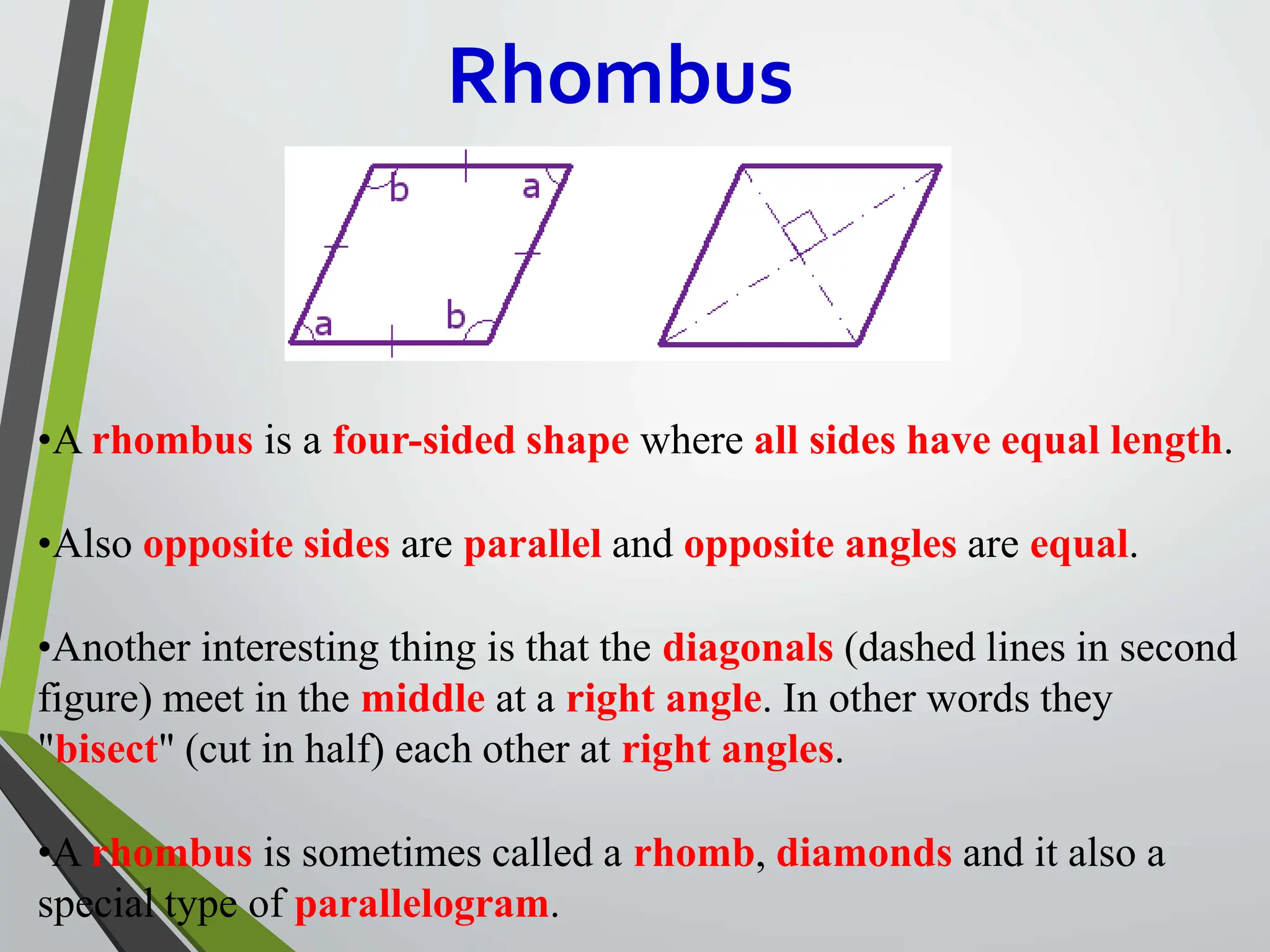
This document defines and provides properties and formulas for various types of quadrilaterals: - A quadrilateral is a flat shape with four straight sides. The interior angles sum to 360 degrees. - Types include parallelograms, rectangles, squares, rhombi, trapezoids, kites. - Formulas are provided for calculating the area and perimeter of each shape based on properties like side length, angles, and diagonals. - Examples demonstrate using the formulas to solve for values like area, perimeter, and diagonal length.

1. QUADRILATERAL
Prepared by:
SHARDA CHAUHAN
TGT MATHEMATICS
CLASS 9

2. What is Quadrilateral?
• Quadrilateral is define as "A flat shape with four sides".
Quadrilateral means four sides.
(Quad means "four" & Lateral means "sides")
Any FOUR-SIDED shape is a Quadrilateral.
But the sides have to be STRAIGHT, and it has to be
2-dimensional (2D).

3. Properties of Quadrilateral
• FOUR sides (edges)
• FOUR vertices (corners)
• The INTERIOR ANGLES add up to 360 degrees
For example :
100°+100°+110°+50°=360° 90°+90°90°+90°=360°
Try drawing a quadrilateral, and measure the angles. They should add up to 360°

4. Types of Quadrilateral
Parallelogram Square
Rectangle

5. Types of Quadrilateral
Trapezium
Rhombus
Kite

6. Rectangl
e
•A rectangle is a four-sided shape where every angle
is a right angle (90°).
•Also opposite sides are parallel and equal length.
•It is also a parallelogram.

7. ➢Rectangle Formula
Area of rectangle : a(base) X b(height)
Perimeter of rectangle : 2(a+b)
For example :
5cm
3cm
Find the area of the rectangle
Area of rectangle : 5cm X 3cm =15cm²
Find the perimeter of the rectangle
Perimeter of rectangle : 2(5cm + 3cm)
= 10cm + 6cm
= 16cm

8. Rhombus
•A rhombus is a four-sided shape where all sides have equal length.
•Also opposite sides are parallel and opposite angles are equal.
•Another interesting thing is that the diagonals (dashed lines in second
figure) meet in the middle at a right angle. In other words they
"bisect" (cut in half) each other at right angles.
•A rhombus is sometimes called a rhomb, diamonds and it also a
special type of parallelogram.

9. ➢Rhombus Formula
Base Times Height Method : Area of Rhombus = b X h
Diagonal Method : Area of Rhombus = ½ X d1 X d2
Trigonometry Method : Area of Rhombus = a² X SinA
Perimeter of Rhombus = 4(a)
where a = side, b = breadth, h = height, d1, d2 are diagonals
For example :
•Given base 3cm height 4cm
BTHM : b X h
3cm X 4cm
= 12cm²
•Given diagonals 2cm and 4cm
DM : ½ X d1 X d2
½ X 2 X 4
= 4cm²
• Given side 2cm and angle 90°
TM : a² X SinA
(2)² X Sin (90°)
= 4 X 1
= 4cm²
• Given side 2cm
Perimeter of Rhombus = 4(2)
= 8cm

10. Square
• A square has equal sides and every angle is a right angle (90°)
• Also opposite sides are parallel.
•A square also fits the definition of a rectangle (all angles are 90°),
and a rhombus (all sides are equal length).

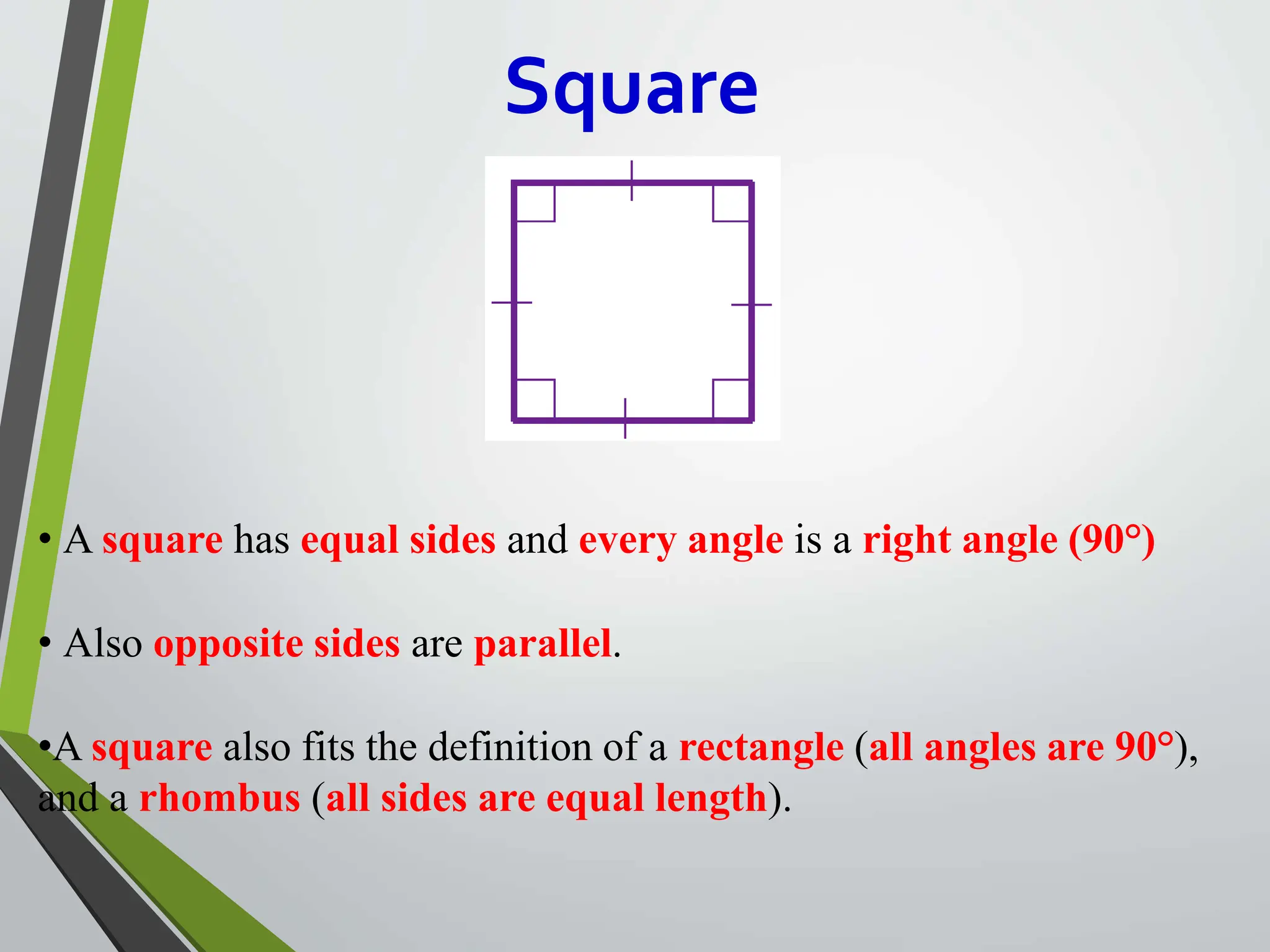
11. ➢Square Formula
Area of Square = (a)²
Perimeter of Square = 4(a)
Diagonal of Square = (a)[sqrt(2)]
where a = side
For example :
3cm Area of Square = (3cm)²
= 9cm²
Perimeter of Square = 4(3cm)
= 12cm
Diagonal of Square = (3cm)[sq.root(2)]
= 3cm(1.414)
= 4.242cm

12. Parallelogram
•A parallelogram has opposite sides parallel and equal in
length.
•Also opposite angles are equal (angles "a" are the same, and
angles "b" are the same).
• NOTE: Squares, Rectangles and Rhombuses are all
Parallelograms!

13. ➢Parallelogram Formula
Area of Parallelogram = b (base) X h (height)
Perimeter of parallelogram = 2a + 2b
For example :
a
b
a
b
Given side a is 3cm side be is 4cm
Perimeter of parallelogram : 2(3cm) + 2(4cm)
= 6cm + 8cm
= 14cm
b
h
Given the base is 3cm and height is 5cm
Area of parallelogram : 3cm X 5cm
= 15cm²

14. Trapezium
• A trapezium (UK Mathematics) has a pair of opposite sides parallel.
•It is called an Isosceles trapezium if the sides that aren't parallel are
equal in length and both angles coming from a parallel side are equal,
as shown.
• A trapezoid has no pair of opposite sides parallel.
Trapezium Isosceles Trapezium

15. AlternateAngle
b
• Trapezium is a special quadrilateral because it has a pair of parallel line.
• If the trapezium has no parallel line, the alternate angles would not be formed.
• ∠a = ∠b , "Z" shape is formed.
•∠ABC + ∠BCD = 180° (The parallel angles match together and it will formed a
180°)
A B
a
C
D

16. ➢Trapezium Formula
Area of Trapezium = ½ X (a + b) X h
where a, b = sides, h = height
Perimeter of Trapezium = a + b + c + d
where a, b, c, d = sides
For example :
•Find the area of trapezium. Given length
b is 3cm and length a is 4cm and height is
2cm.
Area of Trapezium = ½ X (4 + 3) X 2
= ½ X 14
= 7cm²
•Given side a is 3, b is 4, c is 5 and d is 6
Perimeter of Trapezium = 3 + 4 + 5 + 6
= 18cm

17. Kite
• A kite has two pairs of sides.
• Each pair is made up of adjacent sides that are equal in length.
• The angles are equal where the pairs meet.
• Diagonals (dashed lines) meet at a right angle
• The diagonals of a kite are perpendicular.

18. Kite Formula
Diagonal Method : Area of Kite = ½ X d1 X d2
Trigonometry Method:Area of Kite = a X b X SinC
Perimeter of Kite = 2 (a + b)
where a = length, b = breadth, d1, d2 are diagonals
For example :
•Find the area of kite given diagonals 2cm and 4cm
DM : Area of kite = ½ X 2 X 4
= 4cm²
•Given length 2cm and breadth 3cm. Find the area.
TM : Area of kite = 2 X 3 X Sin 90°
= 6cm²
•Given length 2cm and breadth 3cm. Find the
perimeter.
Perimeter of kite = 2 (2cm + 3cm)
= 10cm

19. ComplexQuadrilaterals
When two sides cross over, you call it a "Complex" or
"Self-Intersecting".
For example :
• They still have 4 sides, but two sides cross over.

20. Any Questions?
Thankyou!