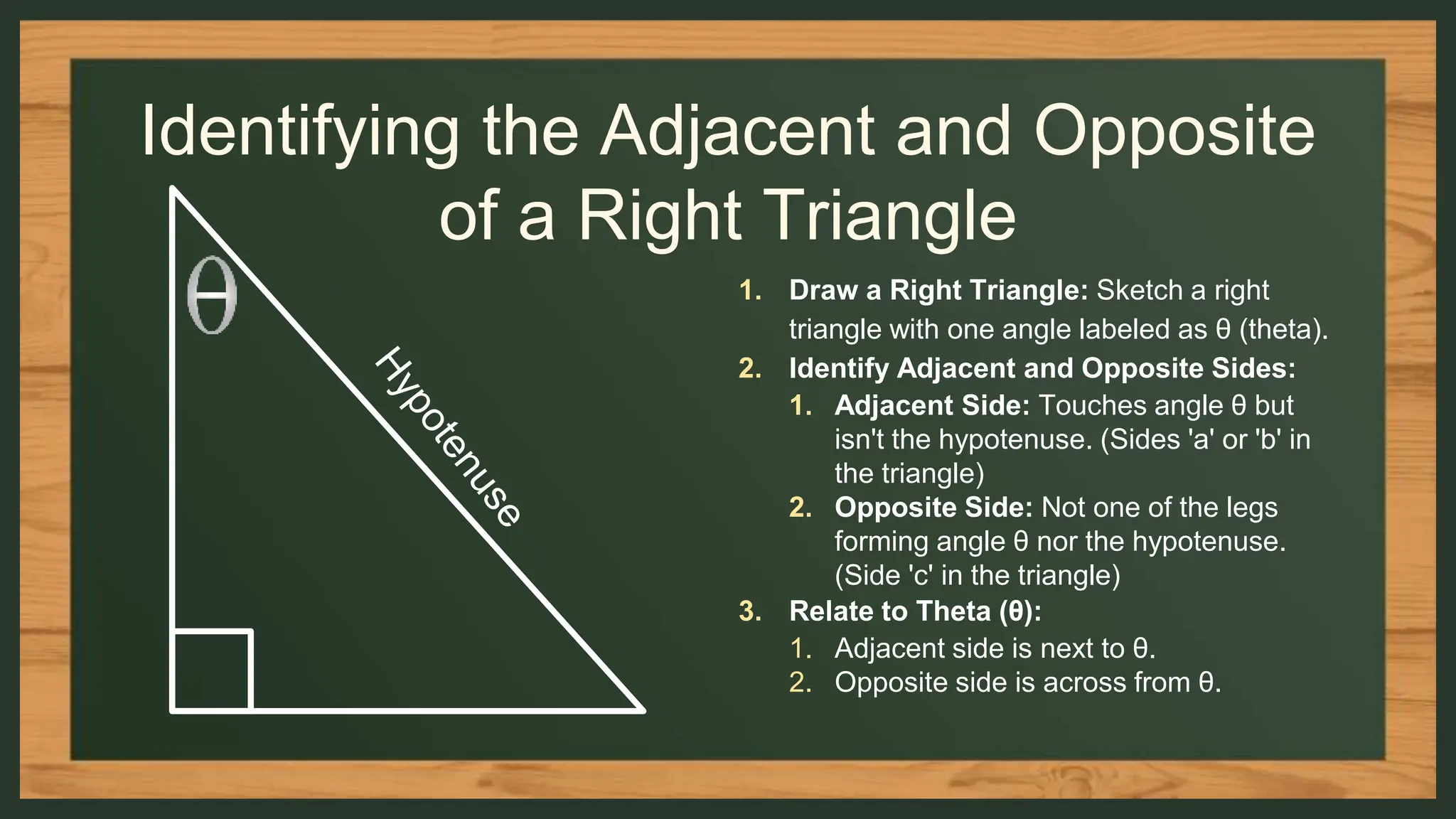
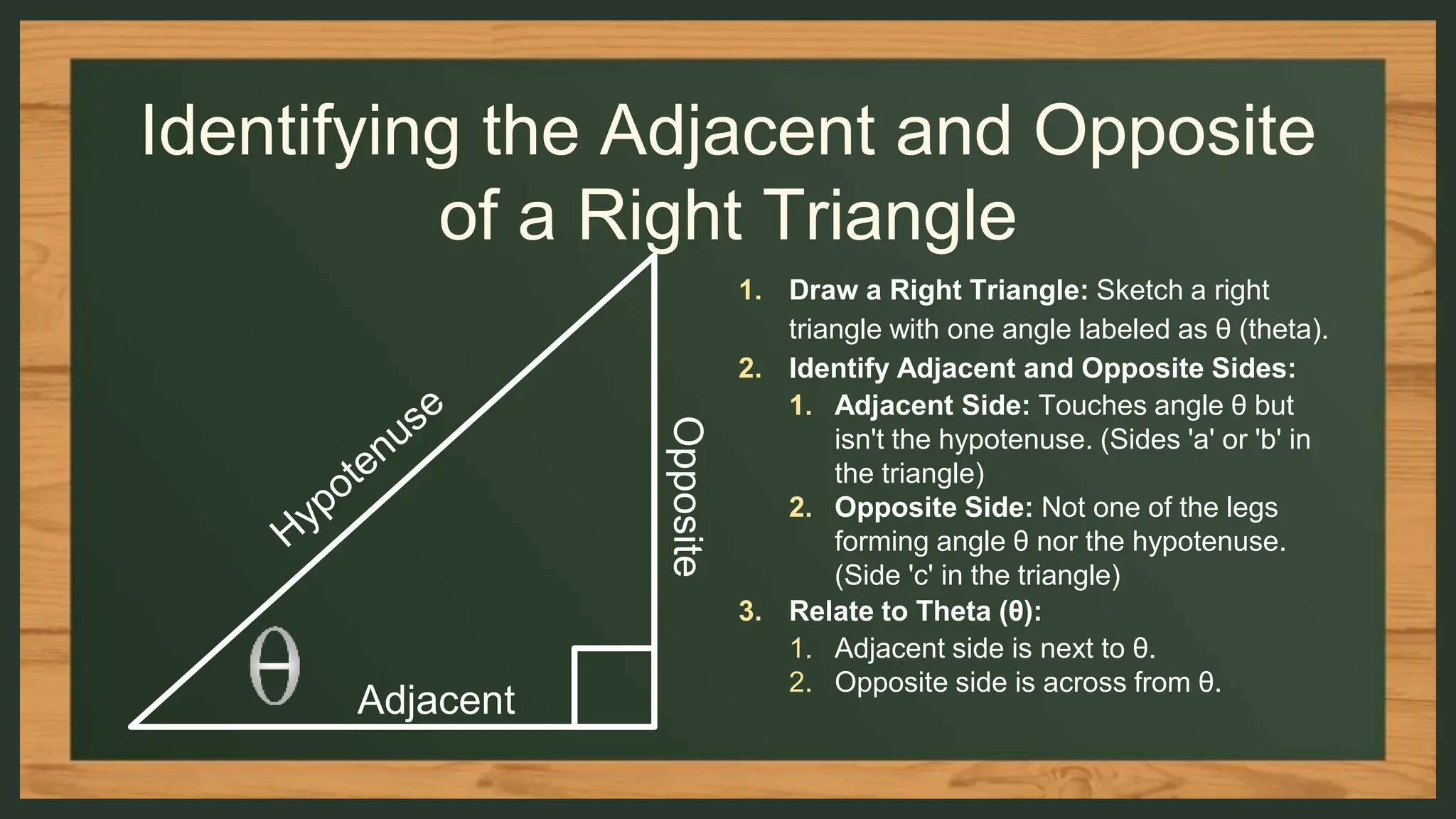
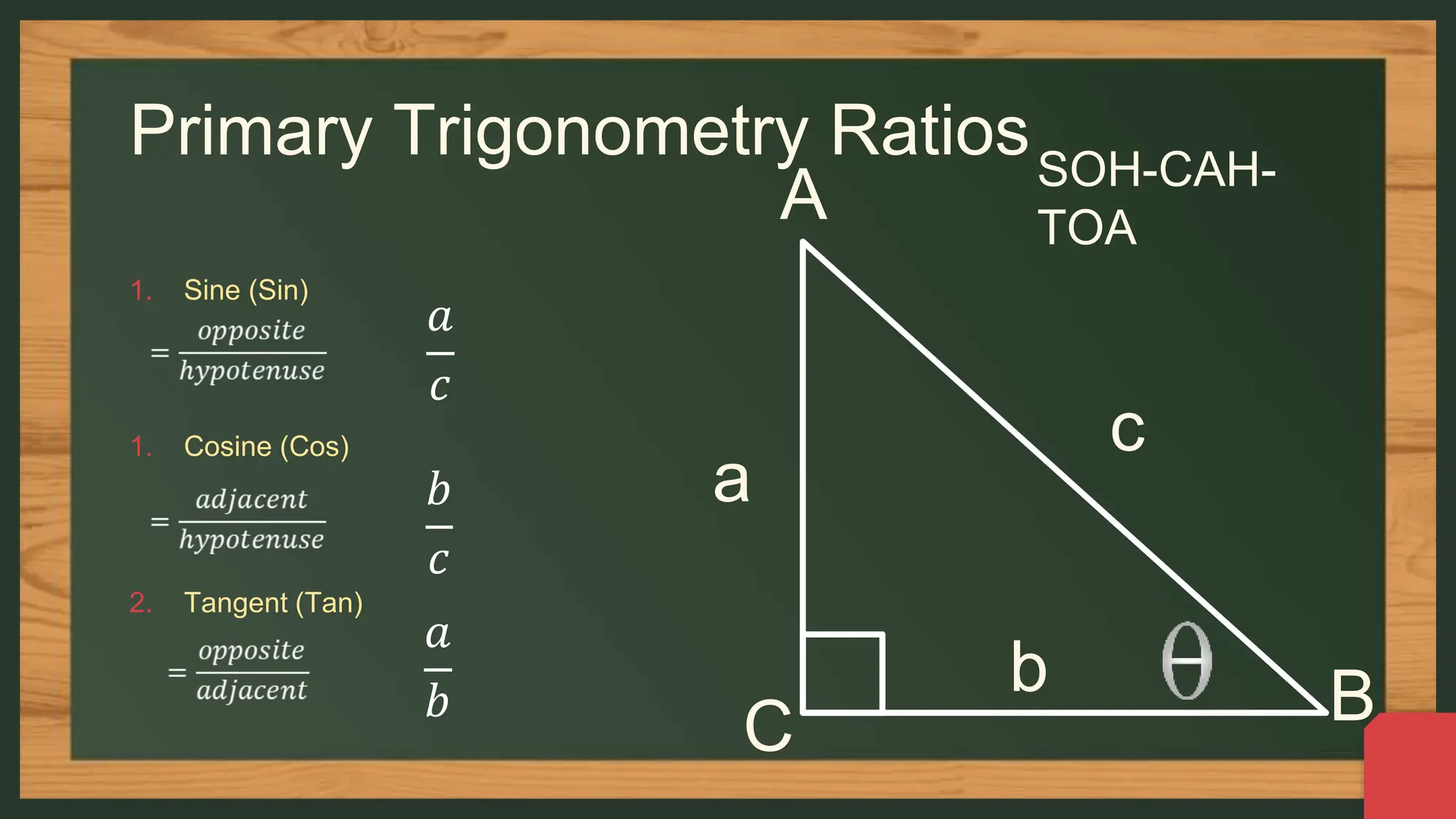
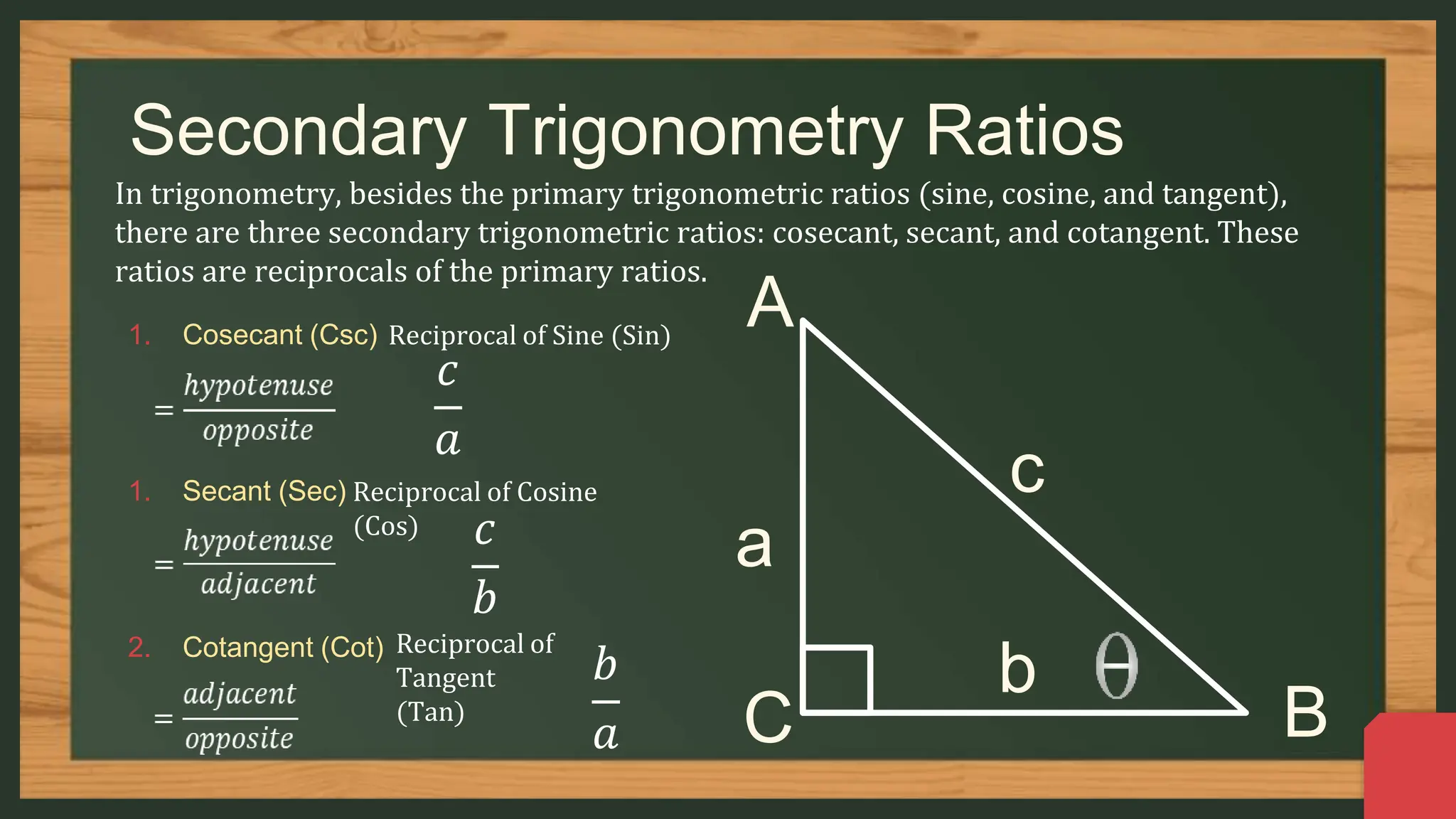
The document provides an overview of the six trigonometric ratios: sine, cosine, tangent, secant, cosecant, and cotangent, aimed at 9th-grade students. It explains the basics of trigonometry, including the identification of sides in right triangles, the use of mnemonic 'SOH-CAH-TOA' for remembering the ratios, and how to apply these concepts in practical situations. Additionally, it includes several examples and assignments to reinforce understanding of these concepts.

1. Trigonometry:
The Six Trigonometry Ratios
Grade 9 Mathematics
-Keizar Paul B. Gonzales
Lesson 1

2. 01 Illustrate the six trigonometric ratios: sine, cosine, tangent, secant,
cosecant, and cotangent;
Objectives
Introduction to Trigonometry Ratios:
02 Find the value of the six trigonometric ratios from the given triangle;
and
Unlocking Trigonometric Secrets:
03 Appreciate the importance of trigonometry in real life situations.
Using Trigonometry in Everyday
Contexts:

3. Trigonometry
9

4. Trigonometry
9

5. Trigonometry
9

6. Trigonometry
9

7. Trigonometry
9

8. Guide
Questions
1. What comes to your mind when you heard about
triangles?
2. In your opinion, How can trigonometry be used in
surveying to measure distances and angles
accurately when mapping land or constructing
buildings?
3. How ancient people discovered Trigonometry?

9. -Trigonometry is a branch of Mathematics that
deals with the relation between the sides and
angles of a triangle.
-From the Greek words “trigonon” trigon meaning
triangle and “metron”, to measure. It is literally
means “ measurement of triangles”.
Trigonometry
-It is a tool used for measuring distances that
cannot be directly measured.
-Trigonometry involves the study of angles and
geometric ratios.
Hipparch
us
Father of Trigonometry

10. Right Triangle Trigonometry
It is often used to find the length of one side or the measure of an acute angle of
a right triangle.
1. Hypotenuse – is always the
side opposite the right angle, it
is the longest side of a right
triangle.
2. Adjacent side – the side which
is also a side of the given
acute angle.
3. Opposite side – The side
opposite the given acute angle.

11. 1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.
How do you know which is Adjacent
and Opposite?
What is Theta (θ)?
Theta (θ) is a symbol used to
represent an angle in
mathematics, particularly in
geometry and trigonometry.
It's like a placeholder for an
unknown or specified angle in
equations and diagrams.

12. 1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.
Identifying the Adjacent and Opposite
of a Right Triangle
Adjacent
Opposite

13. 1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.
Identifying the Adjacent and Opposite
of a Right Triangle

14. 1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.
Identifying the Adjacent and Opposite
of a Right Triangle
Opposite
Adjacent

15. 1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.
Identifying the Adjacent and Opposite
of a Right Triangle

16. 1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.
Identifying the Adjacent and Opposite
of a Right Triangle
Opposite
Adjacent

17. 1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.
Identifying the Adjacent and Opposite
of a Right Triangle

18. 1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.
Identifying the Adjacent and Opposite
of a Right Triangle
Opposite
Adjacent

19. Identifying the Adjacent and Opposite
of a Right Triangle
Hypotenuse
1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.

20. Identifying the Adjacent and Opposite
of a Right Triangle
1. Draw a Right Triangle: Sketch a right
triangle with one angle labeled as θ (theta).
2. Identify Adjacent and Opposite Sides:
1. Adjacent Side: Touches angle θ but
isn't the hypotenuse. (Sides 'a' or 'b' in
the triangle)
2. Opposite Side: Not one of the legs
forming angle θ nor the hypotenuse.
(Side 'c' in the triangle)
3. Relate to Theta (θ):
1. Adjacent side is next to θ.
2. Opposite side is across from θ.
Opposite
Adjacent

21. Primary Trigonometry Ratios
1. Sine (Sin)
1. Cosine (Cos)
2. Tangent (Tan)
A
B
C
a
b
c
SOH-CAH-
TOA
𝑎
𝑐
𝑏
𝑐
𝑎
𝑏

22. Secondary Trigonometry Ratios
1. Cosecant (Csc)
1. Secant (Sec)
2. Cotangent (Cot)
A
B
C
a
b
c
In trigonometry, besides the primary trigonometric ratios (sine, cosine, and tangent),
there are three secondary trigonometric ratios: cosecant, secant, and cotangent. These
ratios are reciprocals of the primary ratios.
Reciprocal of Sine (Sin)
Reciprocal of Cosine
(Cos)
Reciprocal of
Tangent
(Tan)
𝑐
𝑎
𝑐
𝑏
𝑏
𝑎

23. SOH-CAH-TOA
■ S- Sine
■ O – Opposite
■ H- Hypothenuse
■ C – Cosine
■ A – Adjacent
■ H – Hypothenuse
■ T – Tangent
■ O – Opposite
■ A - Adjacent
■ Cosecant –
■ Secant –
■ Cotangent -
Reciprocal of Sine (Sin)
Reciprocal of Cosine
(Cos)
Reciprocal of
Tangent
(Tan)

24. Example
5
Remember the
SOH-CAH-TOA
Step 1. Identify where is the
theta or Degree.
01
37°
3
4
Step 2. Identify where is the
Hypothenuse, Opposite,
Adjacent.
Step 3. Evaluate using
SOH-CAH-TOA
sin 37°
cos 37°
tan 37°
c𝑠𝑐 37°
sec 37°
cot 37°
4
5
3
5
4
3
5
4
5
3
3
4

25. Example
10
Remember the
SOH-CAH-TOA
Step 1. Identify where is the
theta or Degree.
02
37°
8
6
Step 2. Identify where is the
Hypothenuse, Opposite,
Adjacent.
Step 3. Evaluate using
SOH-CAH-TOA
sin 37°
cos 37°
tan 37°
c𝑠𝑐 37°
sec 37°
cot 37°
6
10
8
10
6
8
10
6
10
8
8
6

26. Try This!
13
Remember the
SOH-CAH-TOA
Step 1. Identify where is the
theta or Degree.
03
40°
12
5
Step 2. Identify where is the
Hypothenuse, Opposite,
Adjacent.
Step 3. Evaluate using
SOH-CAH-TOA
sin 40°
cos 40°
tan 40°
c𝑠𝑐 40°
sec 40°
cot 40°
5
13
12
13
5
12
13
5
13
12
12
5

27. Try This!
13
Remember the
SOH-CAH-TOA
Step 1. Identify where is the
theta or Degree.
04
12
5
Step 2. Identify where is the
Hypothenuse, Opposite,
Adjacent.
Step 3. Evaluate using
SOH-CAH-TOA
sin 𝜃
cos 𝜃
tan 𝜃
c𝑠𝑐 𝜃
sec 𝜃
cot 𝜃
5
13
12
13
5
12
13
5
13
12
12
5

28. Example
x
Remember the
SOH-CAH-TOA
Step 1. Identify where is the theta or Degree.
05
24
7
Step 2. Identify where is the Hypothenuse,
Opposite, Adjacent.
Step 3. Evaluate using SOH-CAH-TOA
sin 𝜃
cos 𝜃
tan 𝜃
c𝑠𝑐 𝜃
sec 𝜃
cot 𝜃
7
25
24
25
7
24
25
7
25
24
24
7
Step 3. find the missing value using Pythagorean
Theorem
𝑐 = 𝑎2 + 𝑏2
𝑐 = 72 + 242
𝑐 = 49 + 576
𝑐 = 49 + 576
𝑐 = 625
𝑐 = 25
25

29. Example
06
x
3
10
𝑐 = 𝑎2 + 𝑏2
𝑐 = 32 + ( 10)2
𝑐 = 9 + 10
𝑐 = 19
19

30. Example
06
3
10
19
sin 𝜃
cos 𝜃
tan 𝜃
𝑆𝑂𝐻 − 𝐶𝐴𝐻 − 𝑇𝑂𝐴
10
19
19
19
.
= 3 19
19
3
19
19
19
.
= 190
19
10
3
=

31. Example
06
3
10
19
csc 𝜃
s𝑒𝑐 𝜃
cot 𝜃
𝑆𝑂𝐻 − 𝐶𝐴𝐻 − 𝑇𝑂𝐴
19
10
10
10
.
= 19
3
= 190
10
3
10
= 3 10
10
10
10
.

32. Example
06
3
10
19
csc 𝜃
s𝑒𝑐 𝜃
cot 𝜃
𝑆𝑂𝐻 − 𝐶𝐴𝐻 − 𝑇𝑂𝐴
19
10
10
10
.
= 19
3
= 190
10
3
10
= 3 10
10
10
10
.

33. Assignment
Make an acronym on a piece of Bond paper (any size)
using the trigonometric functions (6): sine, cosine,
tangent, cotangent, secant, and cosecant, that are related
in Math. (No Short Cut)
Example: (Do not copy the example)
S- Statistics
I- Imaginary Numbers
N- Number Theory
E- Exponential

34. —Keizar
“Life is like a trigonometry, every degree
has a different unique answer, but every
situation it becomes theta, when you
leave it, it still unknown for future
situation.